Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок прямування чисел в натуральному рядуСодержание книги
Поиск на нашем сайте
Одночасно з складом числа розглядається натуральне прямування чисел першої сотні: кожне наступне число більше попереднього на 1; кожне попереднє число менше наступного на 1. Виходячи з цього можна повторити й інший спосіб утворення натуральних чисел: прираховуючи або відраховуючи по 1. До рядків чисел, що було запропоновано раніше, можна задати такі запитання: § Прочитай числа другого рядка. § На скільки наступне число 17 більше попереднього 16? (На 1) § Як отримати наступне число 17 із попереднього числа 16? (Треба до 16 додати 1.) § Запишіть відповідний приклад. (17 = 16 + 1) § На скільки попереднє число 12 менше наступного 13? (На 1) § Як отримати число 12 ін наступного числа 13? (Треба відняти 1) § Запишіть відповідний приклад. (12 = 13 – 1) Узагальнити властивості натурального ряду чисел можна за допомогою “казкових” цифр: § Розглянемо рядок “зашифрованих” чисел: А Б В Г Д Е Ж З К. § Назвіть наступне число до числа Е. Навіть попереднє до нього. § Назвіть саме велике число. Назвіть саме мале число. § На скільки число Д більше числа Г? Який висновок можна зробити? (Кожне наступне число більше попереднього на 1) § На скільки число Г менше числа Д? Який висновок можна зробити? (Кожне попереднє число менше наступного на 1) § Як отримати число Д з числа Г? Як отримати число Г з числа Д? Який висновок можна зроби? (Для того, щоб отримати наступне число, треба до попереднього числа додати 1. Для того щоб отримати попереднє число, треба з наступного числа відняти 1.) Зроблені узагальнення можна примінити при розгляданні наступних чисел, наприклад: § Назвіть наступне число до числа 51? (52) На скільки число 52 більше числа 51?... § Як можна отримати число 52 із числа 51? (Треба до числа 51 додати 1) § Назвіть попереднє число до числа 59. На скільки число 58 менше числа 59?... § Як можна отримати число 58 із числа 59? (Треба від числа 59 відняти 1.) Узагальнюється натуральне прямування чисел першої сотні при складанні таблиці першої сотні: За цією таблицею пропонуємо учням запитання: § Прочитайте числа 2-го (6-го, 4-го...) десятка. § Назвіть попереднє число 54. Назвіть наступне число до 58. § Назвіть сусідів числа 45. § Прочитайте всі числа, які містять 7 десятків. Чим вони відрізняються? (В них різне число одиниць) § Прочитайте всі числа, які містять 8 одиниць. Чим вони відрізняються? (В них різне число десятків.) § Порівняйте числа в 7 рядку? На скільки кожне наступне більше за попереднє? На скільки попереднє менше наступного? (На 1). § Порівняйте числа в 5 стовпці. На скільки більше кожне наступне? На скільки менше кожне попереднє?(На 10.) § З чисел третього та четвертого рядку порівняй числа, що записані одне під одним. На скільки верхнє число менше? На скільки нижнє число більше? § Запиши різниці цих чисел. Обчисли їх значення. § Збільш кожне число п'ятого рядку на 10 і запиши отримані числа в наступному рядку. § Прочитай ці числа. З метою засвоєння учнями натурального прямування чисел першої сотні включаються вправи на рахунок предметів, прираховуючи по 1 і по 10, спираючись на наочність. Прикладаються знання натурального прямування чисел при виконанні вправ: 1. Хлопчик мешкає в вісімдесят сьомій квартирі. На кожному поверсі по три квартири. Які ще номери квартир можуть бути на цьому поверсі? 2. Дівчинка стоїть в театрі біля 43 місця, їй потрібно пройти до 37 місця в цьому ж ряді. Повз яких крісел вона повинна пройти? Порівняння чисел Розглянемо способи порівняння чисел: 1. Спосіб на підставі порядку прямування чисел в натуральному ряді: число, яке йде при рахунку пізніше – більше, а число, що при рахунку йде раніше – менше. З цим способом порівняння діти вже добре знайомі; ознайомлення з ним відбулося при вивченні порівняння чисел першого десятку, а закріплення – при вивченні порівняння чисел до 20. Тому, на етапі актуалізації слід повторити, як треба міркувати при порівнянні чисел другого десятку; а потім запитати учнів “Чи можна так само міркувати при порівнянні чисел першої сотні?”; і перенести цей спосіб порівняння в нову ситуацію. 2. Порозрядне порівняння чисел починається з найвищого розряду і відбувається за алгоритмом: 1) підкреслюю число десятків в кожному числі; 2) порівнюю числа десятків: більше те число, в якому десятків більше (менше те число, в якому десятків менше); якщо десятків порівну, то переходжу до п. 3); 3) підкреслюю число одиниць в кожному числі. 4) порівнюю числа одиниць: більше те число, в якому одиниць більше (менше те число, в якому одиниць менше); якщо одиниць порівну, то ці числа рівні. Це новий спосіб порівняння. Він буде широко застосовуватися при порівнянні чисел в усіх подальших концентрах, тому йому слід приділити певну увагу. Письмова нумерація чисел При вивченні письмової нумерації спираємося на уміння учнів записувати числа другого десятка: учні вже знають, що запису чисел другого десятка на першому місці справа наліво пишуть одиниці, а на другому десятки; та на знання десяткового складу чисел першої сотні. Використовуючи абак і пучки паличок та окремі палички повторюємо письмову нумерацію чисел другого десятка. Наприклад, на абаку розкладено 13 паличок: 1 пучок – десяток та 3 окремі палички – одиниці; вчитель запитує: § Яке число позначено в таблиці? (13) § Скільки в ньому десятків? Скільки одиниць? § Позначте це розрізними цифрами. Що означає цифра 3 на першому місці справа? Цифра 1 на другому місці справа? § Візьмемо ще один пучок –десяток. В яку кишеню треба його покласти? Скільки стало десятків? Позначте це карткою з цифрою. § Прочитайте отримане число. (23) § Порівняйте записи чисел 13 та 23. Чим вони схожі? Чому? (Вони схожі тим, що на першому місці справа записана цифра 3, яка означає число одиниць; в обох цих числах однакове число одиниць.) § Чим вони відрізняються? Чому? (В них різні цифри на другому місці, тому що в них різне число десятків.) § Поміняємо картки з цифрами 3 та 2 місцями. Які зміни ми повинні виконати в верхніх кишенях абака? § Які числа ми записували? (Двоцифрові.) § В двоцифрових числах на якому місці пишуть одиниці? Десятки? (В двоцифровому числі на першому місці справа пишуть одиниці, а на другому десятки.) Засвоєнню цього висновку сприяють вправи: 1) поясніть, що означає кожна цифра в запису числа (наприклад: в числі 47 цифра 7 означає кількість одиниць, а цифра 4 – кількість десятків); 2) запишіть за допомогою даних цифр можливі двоцифрові числа (наприклад, з цифр 2 та 5 можна скласти такі двоцифрові числа: 22, 25, 52, 55); 3) дайте характеристику числу: десятковий склад, місце в натуральному ряді, особливості запису (наприклад, число 43 містить 4 десятки та 3 одиниці; попереднє до нього число 42, а наступне – 44; це двоцифрове число записується за допомогою двох різних цифр 4 та 3). Навчання молодших школярів запису чисел першої сотні здійснюється засобом завдань: 1. За допомогою пучків і паличок зобразіть числа, які записуються так: 57, 84, 49, 14. Скільки десятків і одиниць в кожному з них? 2. Розгляньте, як записали числа в нумераційній таблиці. Прочитайте ці числа. 3. Запишіть числа в нумераційній таблиці, в яких: 1 десяток і 7 одиниць; 7 десятків і 7 одиниць, 5 десятків; 4 десятки і 3 одиниці; 7 одиниць; 6 десятків.
4. Запишіть в зошиті числа, які містять 5 дес. і 4 од; 8 дес. 1 од…. 5. Запишіть в зошиті числа: дванадцять вісім, п'ятнадцять, сорок три… 8. Випадки додавання і віднімання Спираємося на знання учнів виконувати аналогічні обчислення в межах 20. Додавання і віднімання числа 1 до будь-якого числа полягає на знанні порядку прямування чисел в натуральному ряді і на знанні і оперування термінами “наступне число” та “попереднє число”. Учні розв'язують приклади з поясненням: 17 + 1 19 + 1 67 + 1 19 – 1 21 – 1 42 – 1 § Розділіть ці приклади на дві групи. На які групи їх можна поділити? (Відокремити можна приклади на додавання 1, і відокремити в окрему групу приклади на віднімання 1. § Як треба міркувати при додаванні числа 1? (Додати 1 – це означає отримати наступне число.) § Як треба міркувати при відніманні числа 1? (відняти 1 – це означає отримати попереднє число.) § Які приклади тут “нові”. Чи можна їх розв'язати за цими правилами? Розв'яжіть нові приклади. При вивченні нумерації чисел від 11 до 20 учні познайомилися з прийомом додавання і віднімання на підставі десяткового складу числа. Тепер його треба перенести в нову ситуацію, на випадки виду: 40 + 7, 57 – 7, 35 – 30. Спочатку актуалізуємо уміння дітей виконувати додавання і віднімання на підставі десяткового складу числа у межах 20, а потім з'ясовуємо чи можна так само міркувати і в нових випадках обчислення. Наприклад, 40 + 7 1. 40 – це 4 десятки. 2. 7 – це 7 одиниць. 3. Було 4 десятки, додали 7 одиниць, отримали 4 десятки і 7 одиниць – це число 47. 40 + 7 = 4д. 7 од. = 47 Наприклад, 57 – 7 1. 57 – це 5 десятків та 7 одиниць. 2. 7 – це 7 одиниць. 3. Було 5 десятків та 7 одиниць, відняли 7 одиниць, залишилося 5 десятків або 50.
Наприклад, 35 – 30 1. 35 – це 3 десятки та 5 одиниць. 2. 30 – це 3 десятки. 3. Було 3 десятки та 5 одиниць, відняли 3 десятки, залишилося 5 одиниць, або просто 5.
З метою формування обчислювальних навичок учням можна пропонувати картки з друкованою основою, типу:
Отже, нами розглянуто методику вивчення нумерації чисел від 21 до 100, в тому числі випадки додавання і віднімання на підставі знань з нумерації. Методика вивчення додавання В теорії укрупнення дидактичних одиниць при вивченні математики, одним із принципів є одночасне вивчення взаємно обернених дій. Отже додавання і віднімання вивчається одночасно і в порівнянні. Це має ряд переваг: по перше є можливість на одному й тому ж уроці виконати перевірку вірності розв'язання (додавання перевірити відніманням, віднімання – додаванням); по-друге – одночасне вивчення додавання і віднімання заощаджує час – витрачається не два уроки, а один урок. Крім того, одночасне виконання взаємно обернених дій розвиває гнучкість розуму, варіативність мислення; а також, знання, які пропонуються в порівнянні засвоюються швидше і міцніше, довше зберігаються у пам'яті. Отже пропонуємо одночасно вивчати окремі випадки додавання і віднімання. При вивченні усного додавання і віднімання можливі два підходи: перший полягає у вивченні спочатку часткових випадків додавання і віднімання, а потім пропонується загальний випадок; за другим – учні відразу знайомляться загальним випадком додавання і віднімання двоцифрових чисел (кожне з них містить і десятки і одиниці) способом порозрядного додавання, а потім з частковими випадками. За першим підходом додавання і віднімання повинно вивчатися у наступному порядку: 1) випадки додавання і віднімання виду: 45 + 2, 45 + 20, 45 – 2, 2) випадки додавання виду: 56 + 4; 3) додавання і віднімання виду 34 + 52 і 76 – 44 (по частинах); 4) додавання і віднімання виду 34 + 52 і 76 – 44 (порозрядно). 4) В підручнику М.В.Богдановича “Математика 2” реалізовано другий підхід, то розглянемо його докладно. Додавання і віднімання виду: Розглянемо методику ознайомлення учнів з способом порозрядного додавання (загальний випадок обидва доданки містять і десятки і одиниці). На етапі актуалізації опорних знань треба повторити: - додавання і віднімання круглих десятків; - додавання і віднімання чисел в межах 10; - переставну властивість додавання при розв'язуванні прикладів: 30 + 4 + 50 + 2; - подання двоцифрових чисел в вигляді суми десятків і одиниць. Знаходячи значення сум чотирьох чисел серед яких два доданки круглі десятки, а два числа – одиниці, учні впевнюються, що зручніше десятки додавати до десятків, а одиниці – до одиниць; і щоб отримати кінцевий результат треба додати отримані числа. Далі на підставі аналізу розв'язаного прикладу, учні дістають висновку про зміст прийомів порозрядного додавання і віднімання і формулюються відповідні пам'ятки.
30+4 50+2 § Як треба міркувати, щоб обчислити значення суми цим способом? Учні коментують розв'язання, і складається алгоритм:
Первинне закріплення цього алгоритму здійснюється при коментуванні учнями розв'язування прикладів. З метою формування умінь і навичок порозрядного додавання учням можна пропонувати картки з друкованою основою типу:
Після засвоєння учнями змісту способу обчислення, міркування можуть скорочуватися, а з ними і запис:
Аналогічно учні знайомляться з загальним випадком віднімання двоцифрових чисел, коли і зменшуване і від'ємник містять одиниці обох розрядів, способом порозрядного віднімання.
Методика формування умінь і навичок аналогічна.
Існує можливість порівняння способів порозрядного додавання і віднімання без переходу через розряд і його узагальнення. Порівнюючи учні визначають спільне: і при додаванні і при відніманні треба кожне число замінити сумою десятків і одиниць; окремо виконати дії з десятками, а потім з одиницями; після цього додати отримані результати. Відмічаються ці дії тим, що в одній ми додаємо десятки чи одиниці, а в іншій – віднімаємо. Узагальнена пам'ятка має вигляд:
Випадки додавання виду: 53 + 40, 53 + 4; Наступний випадок, з яким знайомляться учні – це випадок додавання до двоцифрового числа круглих десятків, або одиниць:
50+4 50+4 На етапі актуалізації до введення цього випадку обчислення треба повторити: - переставну властивість додавання при розв'язуванні прикладів виду: 40 + 6 + 2, 60 + 30 + 3; - додавання круглих десятків; - додавання чисел в межах 10; - подання двоцифрового числа у вигляді суми десятків і одиниць. Можна узагальнити міркування при додаванні круглих десятків та окремих одиниць до двоцифрового числа: Ця дія має таку орієнтувальну основу (ООД):
Аналогічно розглядаються відповідні випадки віднімання. Ознайомлення здійснюється на підставі розглядання та аналізування розв'язаних прикладів і колективного складання пам'ятки. Первинне закріплення відбувається під час розв'язування прикладів коментованим письмом.
70+9
70+9 Можна узагальнити міркування для аналогічних випадків додавання і віднімання:
Далі, аналогічно, розглядаються випадки додавання: 20 + 47. Додавання і віднімання виду: Додавання і віднімання двоцифрових чисел Після розглядання випадків додавання круглих десятків або одиниць до двоцифрового числа вводиться спосіб додавання двоцифрових чисел по частинах:
40+5 На етапі актуалізації опорних знань треба повторити: - десятковий склад двоцифрових чисел; - додавання до двоцифрового числа круглих десятків; - додавання до двоцифрового числа одиниць. Методика ознайомлення і методика формування умінь і навичок аналогічна попереднім. Спосіб віднімання двоцифрових чисел по частинах без переходу через розряд вводиться так само:
30+4 Існує можливість узагальнення способів додавання і віднімання двоцифрових чисел. Учням пропонується порівняти розв'язки прикладів на додавання і на віднімання. Вони встановлюють, що в обох прикладах друге число замінюють сумою десятків та одиниць, в обох способах спочатку виконують дії з десятками, а потім з одиницями. Відрізняються вони тим, що в першому прикладі виконується додавання, а в другому – віднімання. Після цього формулюється узагальнена пам'ятка:
Методика вивчення письмового На етапі актуалізації опорних знань треба повторити десятковий склад двоцифрових чисел, назви розрядів, значення кожної цифри в запису числа; а також порозрядне додавання двоцифрових чисел. На етапі ознайомлення треба обґрунтувати необхідність введення нового прийому обчислення. Учням пропонується обчислити суму чисел:
Учні застосовують прийом порозрядного додавання, але стикаються з тим, що знайти суму отриманих результатів 80 і 16 не просто: треба число 16 замінити сумою десятків і одиниць. Так міркувати дуже довго і складно, тому вчитель показує новий прийом обчислення – письмовий, і іншу форму запису – у стовпчик:
Учні розглядають приклад на додавання стовпчиком в нумераційній таблиці. З'ясовують як підписані числа. Дізнаються, чому не можна залишити 16 одиниць в розряді одиниць: 16 = 1д.6од.; розглядають, як записано результат. Потім вчитель ставить запитання: “З якого розряду треба починати виконувати письмове додавання? Чи можна з розряду десятків? Чому не зручно починати додавання з розряду десятків?”. Починати додавання з розряду десятків не можна, тому що може статися, що ще один десяток перейде від одиниць, тому додавання треба починати з розряду одиниць. Таким чином, учні дістають висновку: двоцифрові числа можна додавати стовпчиком. Доданки записують так: одиниці під одиницями, десятки під десятками. Додавання починають з розряду одиниць, при цьому пам'ятаючи, що 10 одиниць складають 1 десяток; потім додають десятки. Пропонуємо учням таку форму запису прикладів:
Записуємо числа стовпчиком: одиниці під одиницями, десятки під десятками. Додавання починаємо з розряду одиниць: 5 одиниць плюс 8 одиниць, отримаємо 13 одиниць; 13 одиниць – це 1 десяток і 3 одиниці; 3 одиниці пишемо під одиницями, а 1 десяток переходить до десятків; стрілочкою показуємо, що один десяток перейшов до десятків, і додавши десятки його слід врахувати. Додаємо десятки: 6 десятків плюс 2 десятки, отримаємо 8 десятків та ще 1 десяток перейшов, буде 9 десятків; пишімо 9 під десятками. Після введення письмового додавання двоцифрових чисел учнів можна познайомити з письмовим відніманням. Учні повторюють письмовий прийом додавання і перед ними ставиться проблемне запитання, чи можна так само виконувати віднімання – стовпчиком. Спочатку можна розглянути приклад на віднімання без переходу через розряд: тут учні переносять спосіб запису чисел стовпчиком і порядок міркування: спочатку віднімають одиниці, а потім – десятки:
Але наступний приклад, створює проблемну ситуацію:
Записавши числа стовпчиком: одиниці під одиницями, десятки під десятками, учні починають віднімати одиниці, але з 6 одиниць не можна відняти 8 одиниць. Вчитель пропонує зайняти 1 десяток у десятків, показавши це стрілочкою, і роздробити його в одиниці. 1десяток – це 10 одиниць, і ще є 6 одиниць, всього 16 одиниць; від 16 одиниць будемо віднімати 8, отримаємо 8 одиниць, підписуємо результат під одиницями. Переходимо до десятків: було 3 десятки, зайняли 1 десяток, лишилося 2 десятки; 2 десятки мінус 1 десяток, отримаємо 1 десяток; результат запишімо під десятками. При вивченні письмового додавання і віднімання розглядаються як приклади без переходу через розряд, так і приклади на додавання і віднімання двоцифрових чисел з переходом через розряд, а також випадки додавання, коли сума одиниць дорівнює 10; і віднімання, коли треба із 0 одиниць відняти кілька одиниць:
Існує можливість порівняти письмові прийми додавання і віднімання. Спільне в них те, що в обох випадках числа записуються стовпчиком: одиниці під одиницями, десятки під десятками; дії починають з розряду одиниць, а потім переходять до розряду десятків. Відмінне: додаючи одиниці ми стикаємося з тим, що із числа, що отримаємо в сумі можна виділити 1 десяток, тоді 1 десяток переходить до десятків; а при відніманні не завжди можна із одиниць зменшуваного відняти одиниці від'ємника, тоді позичають 1 десяток і роздробляють його в одиниці. Але в кожному разі треба пам'ятати, що 10 одиниць нижчого розряду складають 1 одиницю вищого і навпаки. Таким чином, узагальнена пам'ятка має вигляд:
Також корисно порівняти усні і письмові прийоми додавання і віднімання. Усні прийоми записуються в рядок і дії виконуються, починаючи з вищого розряду – десятків. А письмові прийоми записуються в стовпчик і дії починають виконувати з нижчого розряду – одиниць. Методика вивчення усного додавання При вивченні усного додавання і віднімання з переходом через розряд можливі два підходи: згідно першому – спочатку вивчаються часткові випадки додавання і віднімання з переходом через розряд, а за другим, навпаки, спочатку розглядається загальний випадок, і лише потім часткові випадки. Другий підхід реалізовано у підручнику М.В.Богдановича – це стосується лише додавання; порозрядне віднімання двоцифрових чисел не розглядається. Зазначимо, що додавання і віднімання розглядаються М.В.Богдановичем окремо, але в зв'язку з тим, що в методиці введення обчислювальних прийомів порозрядного додавання і віднімання багато спільного, то ми розглянемо послідовно (спочатку додавання, потім віднімання). Додавання і віднімання виду 64 + 37, 72 – 45. Спочатку учні знайомляться з загальним випадком додавання двоцифрових чисел (кожне число містить і десятки і одиниці) способом порозрядного додавання. Виходячи із змісту ООД цього прийому, на етапі актуалізації слід повторити: - подання двоцифрових чисел у вигляді суми десятків та одиниць; - додавання круглих десятків; - додавання в межах 10; - додавання до круглого числа двоцифрового числа. Всі ці дії повинні бути добре засвоєні дітьми ще до введення способу порозрядного додавання. На етапі підготовчої роботи учням пропонується знаходити значення виразів: 40 + 6 + 30 + 5 40 + 8 + 20 + 9 Учні впевнюються, що зручніше до десятків додавати десятки, а до одиниць – одиниці. Ознайомлення учнів з порозрядним додаванням з переходом через розряд здійснюється на підставі порівняння випадків порозрядного додавання без переходу через десяток:
Діти дістають висновку, що при порозрядному додаванні з переходом через розряд міркуємо так само, як і при порозрядному додаванні без переходу через розряд.
Зазначимо, що існує можливість узагальнення порозрядного додавання двоцифрових чисел з переходом та без переходу через розряд. Учні порівнюють відповідні випадки розв'язання і формулюють узагальнену ООД. Ознайомлення з випадком порозрядного віднімання можна здійснити, так само, на підставі порівняння випадків порозрядного віднімання без переходу та з переходом через розряд. Учні дістають висновку, що коли з одиниць зменшуваного не можна відняти одиниці від'ємника, то зменшуване подають у вигляді суми зручних доданків, а далі йде міркування так само, як і у випадках віднімання без переходу через розряд.
Зазначимо, що можна узагальнити спосіб міркування при порозрядному відніманні без переходу та з переходом через розряд. Випадки додавання виду 38 + 4. Ознайомлення здійснюється на підставі перенесення відомого способу міркування в нову ситуацію. Учням пропонується обчислити значення сум:
§ Як будемо міркувати при обчисленні значення першої суми? § Чи можна так само міркувати при обчисленні значення другої суми? (Так, число 76 треба подати у вигляді суми десятків та одиниць. До одиниць додати другий доданок, і отриманий результат додати до десятків.)
§ Порівняйте розв'язання. Чим вони відрізняються? (В другому прикладі сума одиниць першого доданка і другого доданка дорівнює 11, і до 70 треба вже додавати не 9, а 11, що трохи важче. В результаті ми отримали число наступного десятку.) § В цьому прикладі ми перейшли через десяток. Отже випадки додавання, коли сума одиниць першого доданка і другого доданка більша за 10, називаються випадками з переходом через десяток. § Але спосіб міркування в обох прикладах однаковий: двоцифровий доданок подають у вигляді суми десятків та одиниць, другий доданок додають до одиниць, і отриманий результат додають до десятків. Зазначимо, що корисно порівняти цей випадок додавання з “загальним” випадком порозрядного додавання.
Спільне: в обох випадках одиниці додаються до одиниць. Відмінне: в загальному випадку – обидва доданки подаються у вигляді суми десятків та одиниць; у даному випадку – лише перший доданок, тому що другий доданок – одиниці; в загальному випадку десятки додають до десятків, а в даному – ні, тому що другий доданок не містить десятки; в загальному випадку – потім додаються отримані результати, а в даному – число, отримане після додавання одиниць додається до десятків. Випадки додавання виду 38 + 2, 38 + 12. На наступному уроці пропонується додавання до двоцифрового числа одноцифрове число, коли в результаті додавання одиниць отримаємо 10. ООД цього способу міркування таке саме, як і в попередньому випадку:
Корисно порівняти обидва випадки додавання. Спільне в них те, що в кожному двоцифрове число подається у вигляді суми десятків і одиниць, потім одиниці додають до одиниць і додають отриманий результат до десятків. Відрізняються тим, що в першому випадку в результаті додавання одиниць отримали двоцифрове число, яке містить і десятки і одиниці, а в другому – 10. Далі вивчається випадок додавання двоцифрових чисел (обидва містять і десятки і одиниці), коли в результаті отримаємо кругле число, способом порозрядного додавання. На етапі актуалізації треба повторити: - порозрядне додавання двоцифрових чисел (загальний випадок); - додавання одноцифрового числа до двоцифрового, коли сума одиниць рівна 10. Дія виконується за алгоритмом порозрядного додавання (загальний випадок):
Корисно порівняти цей випадок додавання і “загальний” випадок порозрядного додавання. В них багато спільного: обидва числа замінюються сумою десятків та одиниць; спочатку додаються десятки, а потім одиниці; додаються отримані результати. Відмінність полягає в тому, що в загальному випадку в результаті додавання одиниць отримаємо двоцифрове число, яке містить і десятки і одиниці, а в даному випадку – число 10. Також можна порівняти цей випадок додавання з випадком додавання одноцифрового числа до двоцифрового, коли в результаті додавання одиниць отримаємо 10. Спільне: в результаті додавання одиниць отримаємо 10. Відмінне: в даному випадку обидва доданки замінюються сумою десятків та одиниць, а в попередньому – лише перший доданок, тому що другий доданок містить лише одиниці; в даному випадку десятки додаються до десятків, а в попередньому випадку – ні, в другому доданку немає десятків; в даному випадку знаходять суму отриманих результатів після додавання десятків і після додавання одиниць – 10, а в попередньому – до десятків додають число, яке є результатом додавання одиниць – 10. Додавання двоцифрових чисел Існує два способи додавання двоцифрових чисел з переходом через розряд по частинах: Перший – коли один із доданків замінюється сумою десятків та одиниць. Другий – коли один із доданків замінюється сумою зручних доданків. Що стосується першого способу, то він виконується так само, як і для випадків без переходу через розряд. Розглянемо докладно другий спосіб додавання по частинах. На етапі актуалізації опорних знань учні доповнюють двоцифрові числа до круглих (37 + 3 = 40, 42 + 8 = 50) і пригадують, як можна міркувати при обчисленні суми чисел 7 та 6. Вчитель записує на дошці спосіб обчислення по частинах:
На етапі ознайомлення, перед учнями ставиться проблемне запитання “Чи можна застосувати цей спосіб обчислення для зна
§ Як ми міркували при розв'язанні другого прикладу? (Ми другий доданок замінили сумою зручних доданків, так щоб перший доданок доповнити до круглого числа. Доповнили перший доданок до круглого числа, а потім до нього додали решту одиниць.)
Чи можна так само при обчисленні суми чисел 37 та 26?
§ Як ми міркували при обчисленні третього прикладу?
Порівняйте всі три приклади. Що спільного в їх розв'язаннях? (В усіх прикладах ми подавали другий доданок у вигляді зручних доданків; доповнювали перший доданок до круглого числа і додавали до круглого числа іншу частину другого доданка.) Віднімання виду 30 – 3. Після цього вивчається віднімання одноцифрового числа з круглих десятків способом порозрядного віднімання (частний випадок): 10 – 3; 30 – 3; 60 – 3. Орієнтувальна основа порозрядного віднімання для цього випадку обчислення аналогічна випадкам, які розглядалися в межах 20, тому ООД треба перенести в нову ситуацію. Таким чином, на етапі актуалізації треба повторити: - випадки віднімання із числа 20 одноцифрових чисел; - подання круглих чисел у вигляді суми зручних доданків, один із яких дорівнює 10. Учні розв'язують приклад: 20 – 7. 20 – 7 = 10 + 10 – 7 = 10 + 3 = 13
10+10 § З якого числа зручно відняти 7? (З 10) § Тому число 20 ми подали у вигляді суми, яка містить число 10. § А число 30, як замінити у вигляді суми, яка б містила число 10? (30 = 20 + 10) § Нехай треба відняти від 30 число 7. Як будемо міркувати? (Треба число 30 подати у вигляді суми, яка б містила число 10: 30=20+10. Число 7 віднімемо із 10, отримаємо 3; до числа 20 додамо 3, буде 23.) 30 – 7 = 20 + 10 – 7 = 20 + 3 = 23
20+10 § Чим ці приклади схожі? (В однаковий від'ємник – число7, і для того, щоб відняти число 7, зменшуване замінювали такою сумою, яка містить число 10.) § Таку суму будемо називати сумою зручних доданків. § Розв'яжіть приклад. Чи можна так само міркувати? 30 – 5 = 20 + 10 – 5 = 20 + 5 = 25
20+10 § Порівняйте всі ці приклади. Що в них спільного? (Зменшуване замінили сумою зручних доданків, один із яких 10. Від 10 відняли від'ємник і додали отриманий результат до десятків, що залишилися.)
Віднімання виду 53 – 8. Через урок учні розглядають наступний випадок: віднімання одноцифрового числа із
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.191 (0.014 с.) |

 57 – 7 = 5 д. 7 од. – 7 од. = 5д. = 50
57 – 7 = 5 д. 7 од. – 7 од. = 5д. = 50 35 – 30 = 3 д. 5 од. – 3д. = 5 од. = 5
35 – 30 = 3 д. 5 од. – 3д. = 5 од. = 5





 34 + 52 = 30 + 4 + 50 + 2 = 80 + 6 = 86
34 + 52 = 30 + 4 + 50 + 2 = 80 + 6 = 86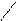
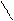










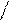









 54 + 30= 50 + 4 + 30 = 80 + 4 = 84, 54 + 3= 50 + 4 + 3 = 50 + 7 = 57.
54 + 30= 50 + 4 + 30 = 80 + 4 = 84, 54 + 3= 50 + 4 + 3 = 50 + 7 = 57.








 79 – 4 = 70 + 9 – 4 = 70 + 5 = 75
79 – 4 = 70 + 9 – 4 = 70 + 5 = 75




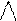




 53 + 45 = 53 + 40 + 5 = 93 + 5 = 98
53 + 45 = 53 + 40 + 5 = 93 + 5 = 98



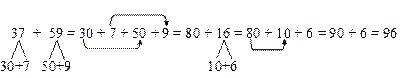



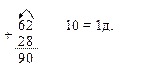





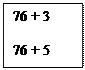


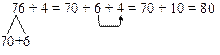


 ходження суми 37 і 6?”.
ходження суми 37 і 6?”.