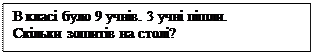Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зміст курсу математика 2-го класуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Зміст курсу математика 2-го класу Програма з математики 2-го класу будується по основним лініям, визначеним Державним стандартом початкової загальної освіти: 1. Числа і дії над ними: - додавання і віднімання в межах 20; - числа 1-100, та число 0; - додавання і віднімання, пов'язані з нумерацією чисел; - додавання і віднімання двоцифрових чисел без переходу через десяток; - додавання і віднімання двоцифрових чисел з переходом через десяток. 2. Табличне множення чисел 2, 3 і ділення на 2, 3. 3. Числові і буквені вирази: - читання і запис; - значення числового виразу; - дужки; - порядок виконання дій у виразах з дужками та без дужок; - перевірка дій додавання і віднімання; - вираз, що містить одну букву та його числове значення; - числові рівності і нерівності. 4. Задачі: - прості; - складені; - обернені задачі. 5. Величини та одиниці вимірювання величин: - одиниці вимірювання довжини; - одиниці вимірювання маси; - одиниці вимірювання часу; - одиниці вимірювання вартості. 6. Геометричні фігури: - багатокутники: трикутник, чотирикутник; - кути многокутника; - прямий кут; - прямокутник; - квадрат; - коло, круг; - позначення геометричних фігур буквами. Виходячи із Державного стандарту підручник “Математика 2” містить такі теми: 1. Повторення матеріалу за 1 клас. 2. Додавання і віднімання чисел з переходом через десяток у межах 20. 3. Нумерація чисел 21-100. 4. Додавання і віднімання двоцифрових чисел без переходу через десяток. 5. Додавання і віднімання двоцифрових чисел з переходом через десяток. 6. Письмове додавання і віднімання двоцифрових чисел. 7. Множення і ділення. Таким чином, в даному посібнику ми розглянемо методику вивчення даних тем, а також методику роботи над задачами, алгебраїчний і геометричний матеріал та величини в курсі математики 2-го класу. Узагальнення та систематизація знань В курсі математики першого класу були вивчені такі змістовні лінії: нумерація чисел до 20; арифметичні дії додавання і віднімання в межах 10, та в межах 20 на підставі знань з нумерації; прості задачі п'ятьох видів; елементи алгебри: простіші числові вирази – сума та різниця, числові вирази більш складної структури – вирази, які містять кілька чисел, що поєднані однаковими або різними знаками арифметичних дій, числові рівності та нерівності; елементи геометрії: поняття “геометрична фігура”, точка, пряма, крива, ламана лінії, промінь, відрізок, трикутник, чотирикутник, п'ятикутник, шестикутник. Таким чином, під час повторення матеріалу за 1-й клас слід систематизувати та узагальнити знання з визначених змістовних ліній. Розглянемо докладно методику узагальнення і систематизації знань. Нумерація чисел Мета: узагальнити та систематизувати знання учнів з нумерації чисел в межах 20: § повторити пряму та обернену послідовність чисел в межах 20; § узагальнити поняття “одноцифрове” та “двоцифрове” число; § узагальнити утворення чисел способом прирахування по одиниці; § актуалізувати утворення чисел другого десятку з одного десятку та кількох одиниць; § узагальнити поняття “склад числа”, актуалізувати десятковий склад чисел другого десятку; § повторити позиційний принцип запису чисел другого десятку. § повторити подання чисел другого десятку у вигляді суми десятка та одиниць; § узагальнити та систематизувати способи порівняння чисел; § систематизувати випадки додавання і віднімання на підставі нумерації та прийому укрупнення розрядних одиниць. З метою актуалізації, узагальнення та систематизації визначених знань можна запропонувати учням завдання: Уважно розгляньте ряд чисел. Розбийте його на дві групи. Яку ознаку покладено в основу класифікації? 9, 12, 5, 10, 7, 0, 14, 18, 2, 11, 19, 1, 8, 13, 4, 17, 3, 15, 6, 16. В основу класифікації покладено ознаку – кількість цифр в запису чисел. Таким чином учні розбивають числа на дві групи, виписуючи числа в порядку зростання: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. 10, 11, 12, 13, 14, 15, 16, 17, 18, 19. Далі учням пропонується узагальнити числа першого ряду, і вони називають їх одним словом – “одноцифрові числа”, тому що для їх запису використана лише одна цифра. Узагальнюючи числа другого ряду визначаємо, що для їх запису використано дві цифри, тому ці числа “двоцифрові”. Можна запропонувати учням відтворити всі одноцифрові числа в порядку спадання; відтворити послідовність прямування чисел другого десятку в порядку спадання. Крім того, згадати поняття “натуральне число”. Натуральні числа – це числа, які застосовуються при рахунку предметів або при порядковому рахунку. Серед даних чисел є зайве число – це число нуль, яке не є натуральним числом. Виключивши число нуль з даної групи чисел, маємо лише натуральні числа. Ці числа ми вже розбили на дві групи: одноцифрові та двоцифрові. Далі можна з'ясувати, яке число є найменшим натуральним числом, яке число є найменшим одноцифровим числом, найбільшим одноцифровим числом, найменшим двоцифровим числом. Обговорюємо питання: “Чим відрізняються двоцифрові числа від одноцифрових?”. Отже, одноцифрові числа відрізняються від двоцифрових тим, що для запису перших використовується лише одна цифра, а для запису других – дві цифри. А що спільного у одноцифрових та двоцифрових чисел? І одноцифрові і двоцифрові числа записуються за допомогою одних й тих самих цифр. Учні називають і записують відомі їм десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Далі можна розповісти учням казку про суперечку нуля з іншими цифрами: цифри звинувачували нуль в тому, що він означає пусту множину предметів, тобто “нічого”, на що нуль відповів: “Якщо я стану праворуч від кожної від вас, то я вас збільшую в десять разів”. Нуль став поруч з одиницею і з'явилося число десять... Але ж цифрам все ж таки хотілося посперечатися, і вони стали сперечатися одна одною: та дев'ятка заявила, що вона найбільша; на що одиниця відповіла: “Якщо я стану ліворуч від тебе, то я буду більше за тебе”. Стала одиниця ліворуч від дев'ятки, і з'явилося число 19. В числі 19 цифра 1 означає 1 десяток, а цифра 9 – лише 9 одиниць! І одиниця почала становитися ліворуч від кожної цифри, так з'явилися числа: 18, 17, 16, 15, 14, 13, 12, 11. Діти визначають значення кожної цифри в запису цих чисел. Який висновок можна з цього зробити? (Саме головне – місце цифри в запису чисел. На першому місці справа наліво пишуться одиниці, а на другому – десяток. 1 десяток = 10 одиницям. Отже, десяток старшій за будь-яке число одиниць.
десяток одиниці В десятковій системі числення 10 одиниць утворюють 1 десяток. Десятки можна лічити, як прості одиниці. Полічимо одиниці. Полічимо десятки: 1 2 3 4 5 6 7 8 9 1д. 2д. 3д. 4д. 5д. 6д. 7д. 8д. 9д. Порівнюємо ряди чисел. В них спільне те, що ми рахували: 1, 2, 3... Відмінне: в першому рядку ми рахували одиниці, а в другому – десятки. Повторюємо утворення чисел другого десятку: вчитель відраховує 10 паличок і зв'язує їх у пучок – десяток; накладаючи на десяток 1, 2, 3... окремі палички, отримуємо числа одинадцять, дванадцять, тринадцять.... Далі можна запропонувати порівняти стовпчики чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9. 11, 12, 13, 14, 15, 16, 17, 18, 19. В кожному стовпчику спільне число одиниць, а відмінне те, що в числах другого рядку є ще й 1 десяток. Яке число більше, і на скільки більше? Яке число менше і на скільки? Отже, кожне число другого стовпчику на 10 одиниць більше за перше число; кожне перше число на 10 одиниць менше за друге число. Потім учні порівнюють числа в кожному рядку: кожне наступне число більше за попереднє на 1, кожне попереднє менше наступного на 1. Як можна отримати кожне наступне число з попереднього? (Треба до попереднього додати 1.) Як отримати попереднє число з наступного? (Треба від наступного числа відняти 1.) Скількома способами можна утворити числа першого рядку? (Двома: прирахуванням 1 до попереднього або відрахування 1 від наступного.) Кількома способами можна утворити числа другого рядку? (Трьома: прирахуванням 1 до попереднього або відрахування 1 від наступного; з 1 десятку та кількох одиниць.) Далі учні читають числа, записані в нумераційній таблиці:
А потім записують числа в нумераційній таблиці: числа, які містять 1 десяток і 6 одиниць, 8 одиниць, 1 десяток, 1 десяток і 9 одиниць; п'ятнадцять, сім, дванадцять, одинадцять...
В зв'язку з тим, що двоцифрові числа містять і десятки і одиниці, то їх можна подати у вигляді особливої суми – суми одного десятку та кількох одиниць. Учням пропонується завдання: “Подати числа у вигляді суми десятків та одиниць”:
Отже, характеризуючи числа другого десятку треба називати не лише попереднє і наступне числа, визначати спосіб його утворення, його десятковий склад, а й подавати число у вигляді суми десятків та одиниць. Далі учні дають характеристику числам, наприклад: 14, 19,10... Чи можна подати у вигляді суми десятків та одиниць число 7? Чому? А у вигляді якої суми можна подати число 7? Запишіть усі випадки складу числа 7.
Запишіть всі випадки складу числа 12.
Обговорюємо з учнями питання: Чим відрізняються числа 7 та 12? (7 – одноцифрове, 12 – двоцифрове.) Чим відрізняються склади цих чисел? (До складу числа 7 входять лише зручні доданки, а до складу числа 12 крім зручних, є й ще особливий випадок: 10+2 – це сума десятків та одиниць, отже число 12 має десятковий склад.) Який висновок можна зробити? (На відміну від одноцифрових чисел, двоцифрові числа мають десятковий склад, тому що їх можна отримати з десятків та одиниць.) Далі актуалізуємо способи додавання і віднімання на підставі нумерації Учням пропонується розбити вирази на групи по способу обчислення: 14 + 1 17 – 10 10 + 2 20 – 1 15 – 5 17 – 7 19 + 1 12 – 10 10 + 8 12 – 1 10 + 3 12 – 2 17 + 1 14 – 10 19 – 1 § Прочитайте перший вираз (14 + 1). Що означає до числа додати 1? Чи є ще такі вирази? Запишіть їх окремо. § Прочитайте другий вираз (17 – 10). Як треба міркувати при обчисленні його значення? Чи є ще такі вирази? Запишіть їх окремо. Так само працюємо з рештою прикладів першого рядку. Таким чином учні розбивають вирази на наступні групи: 14 + 1 20 – 1 10 + 2 17 – 10 15 – 5 19 + 1 12 – 1 10 + 8 12 – 10 17 – 7 17 + 1 19 – 1 10 + 3 14 – 10 12 – 2 Далі узагальнюємо способи обчислення кожної групи прикладів. § Що спільного у виразів першої групи? (В цих сумах однаковий другий доданок – 1.) Що означає до числа додати 1?
§ Знайдіть значення виразів першої групи. § Що спільного у виразів другої групи? (В цих різницях однакові від'ємники – 1.) Що означає від числа відняти 1?
§ Знайдіть значення виразів другої групи. § Що спільного у виразів третьої групи? (Усі суми містять перший доданок, число 10, а другий доданок – окремі одиниці.) Знайдіть значення виразів третьої групи. Як треба міркувати, щоб до десяти додати окремі одиниці?
§ Уважно розгляньте вирази четвертої групи. Що в них спільного? (Усі різниці мають двоцифрове зменшуване, яке містить і десятки і одиниці, а від'ємник в усіх різницях однаковий – число 10.) § Знайдіть значення виразів четвертої групи. Як треба міркувати, що із двоцифрового числа, яке містить і десятки і одиниці відняти 10?
§ Уважно розгляньте вирази п'ятої групи. Що в них спільного? (В усіх різницях зменшуване двоцифрове число, яке містить і десятки і одиниці, а від'ємник – одноцифрове число. При чому від'ємник – це одиниці зменшуваного.) § Знайдіть значення виразів п'ятої групи. Як треба міркувати, щоб від двоцифрового числа відняти його одиниці?
§ Наведіть приклади на кожний з способів обчислення. § Запишіть результати в порядку зростання: від меншого числа до більшого. § Учні отримують такий запис: 2, 4, 7, 10, 11, 12, 13, 15, 18, 19, 20. § Чому 7 більше за 4? (Тому що число 7 при рахунку йде пізніше, ніж 4.) § Чому 2 менше 4? (Тому, що число 2 при рахунку називається раніше, ніж 4.) § Як треба міркувати при порівнянні чисел?
§ Порівняйте числа 9 та 11; 6 та 14, 15 та 7. Що цікавого ви помітили?
§ Який спосіб порівняння чисел ми використовуємо завжди, для будь-яких чисел? (Спосіб порівняння на підставі прямування чисел при рахунку (в натуральному ряді.) § Як ми міркуємо при порівняння одноцифрового та двоцифрового числа? Отже ми узагальнили і систематизували знання учнів з нумерації чисел. Опорний конспект 1
§ Прочитайте приклади третього стовпчика. За якою ознакою їх відокремили? З яких двох чисел складається число 3? Як можна міркувати, щоб додати число 3? (Щоб додати 3, можна спочатку додати 2 а потім 1; а можна по-іншому: спочатку додати 1, а потім 2.) Скількома способами можна додати число 3? (Двома.) Чому? (Число 3 містить два випадки складу числа.) Обчисліть значення цих виразів. § Прочитайте приклади четвертого стовпчика. За якою ознакою їх відокремили? Скількома способами можна відняти число 3? Як можна міркувати, щоб відняти число 3? (Можна спочатку відняти 2, а потім 1; або спочатку відняти 1, а потім 2.) Обчисліть значення цих виразів. § Прочитайте приклади п'ятого стовпчика. За якою ознакою їх відокремили? З яких двох чисел складається число 4? Скількома способами можна додати число 4? Чому? Як можна міркувати при додаванні числа 4? (Можна міркувати так: спочатку додати 3, а потім 1; або додати 2 та ще 2; або додати 1, а потім 3.) Обчисліть значення виразів. § Прочитайте приклади шостого стовпчика. За якою ознакою їх відокремили? Скількома способами можна відняти число 4? Як можна міркувати при віднімання числа 4? (Можна відняти 3, а потім ще 1; або відняти 2 і ще раз 2; або відняти 1, а потім ще 3.) Обчисліть значення виразів. § Прочитайте приклади шостого стовпчика. За якою ознакою їх відокремили? З яких двох чисел складається число 5? Скількома способами можна додати число 5? Чому? Як можна міркувати при додавання числа 5? (Можна спочатку додати 4, а потім додати ще 1; або додати 3 і ще додати 2; або спочатку додати 2, а потім ще 3; або додати 1 і ще 4.) Обчисліть значення виразів. § Прочитайте приклади сьомого стовпчика. За якою ознакою їх відокремили? Скількома способами можна відняти 5? Чому? Як можна відняти 5? (Можна спочатку відняти 4, а потім відняти 1; або спочатку відняти 3, а потім відняти 2; або спочатку відняти 2, а потім ще відняти 3; або спочатку відняти 1, а потім ще 4.) Обчисліть значення виразів.
§ Що спільного у способах міркування додавання чисел 2, 3, 4, 5? Чому число 2 можна додати лише одним способом? Чому число 5 можна додати чотирма способами? На підставі чого ми визначали способи додавання? (На підставі складу числа.) На підставі складу числа, ми число 2 (3, 4, 5) заміняли сумою; і почергово додавали спочатку перший доданок, а потім другий доданок. Отже, числа 2, 3, 4, 5 ми додавали по частинах на підставі складу числа. Як же треба міркувати при додаванні чисел 2, 3, 4, 5? § Що спільного у способах міркування при відніманні чисел 2, 3, 4, 5? Чому число 2 можна відняти лише одним способом? Чому число 5 можна відняти чотирма способами? На підставі чого ми визначали способи віднімання? (На підставі складу числа.) На підставі складу числа, ми число 2 (3, 4, 5) заміняли сумою; і почергово віднімали спочатку перший доданок, а потім другий доданок. Як ми віднімали числа 2, 3, 4, 5? (Ми віднімали по частинах на підставі складу числа.) Як же треба міркувати при відніманні чисел 2, 3, 4, 5?
§ Уважно розгляньте приклади 9-го, 11-го, 13-го та 15-го стовпчиків. Що спільного у способах додавання чисел 6, 7, 8, 9? (В усіх цих прикладах ми міняли місцями доданки: зручніше до більшого числа додавати менше число.) В чому полягає прийом додавання чисел 6, 7, 8, 9?
§ Уважно розгляньте приклади 10-го, 12-го, 14-го та 16-го стовпчиків. Що спільного в способах міркування? (Кожний раз зменшуване замінювали сумою зручних доданків, так щоб другий доданок дорівнював від'ємнику. Далі ми міркували так: якщо від суми двох чисел відняти другий доданок, то залишиться перший доданок.) § Таким чином, ми застосовували при обчисленні цих різниць взаємозв'язок між додаванням і відніманням. Отже, нами застосований прийом віднімання на підставі взаємозв'язку дій додавання і віднімання. Як треба міркувати при цьому?
§ Які числа ми віднімаємо на підставі взаємозв'язку між діями додавання і віднімання. § Наведіть приклади на віднімання, коли треба застосовувати взаємозв'язок між діями додавання і віднімання.
§ Повернемося до виразів, що були подані для класифікації. На скільки груп можна їх тепер розбити? (На чотири: на дві групи можна розбити приклади на додавання і на дві групи можна розбити приклади на віднімання.) § Які приклади на додавання ми віднесемо до першої групи? (Це приклади на додавання по частинах чисел 2,3,4,5.) § Які приклади на додавання ми віднесемо до другої групи? (Приклади, в яких треба застосувати переставну властивість дії додавання: на додавання 6,7,8,9.) § Які приклади на віднімання ми віднесемо до третьої групи? (Приклади на віднімання чисел по частинах: 2,3,4,5.) § Які приклади на віднімання ми поєднаємо у четверту групу? (Приклади, в яких треба застосувати взаємозв'язок між діями додавання і віднімання. Це приклади на віднімання чисел 6, 7, 8, 9.) Таким чином, учні отримують запис:
Отже, нами узагальнені і систематизовані знання учнів про арифметичні дії додавання і віднімання і обчислювальні прийоми додавання і віднімання в межах 10. Прості задачі Методика введення нового порядку роботи В 2-му класі продовжується робота по формуванню умінь розв'язувати вже розглянуті п'ять видів простих задач: 1. Задачі на знаходження суми. 2. Задачі на знаходження остачі. 3. Задачі на збільшення, або зменшення числа на декілька одиниць. 4. Задачі на різницеве порівняння. 5. Задачі на знаходження невідомого доданка. Зазначимо, всі прості задачі в 2-му класі розбираються за пам'яткою №2 для розв'язання простих задач (стор. 16). Але робота над задачею за пам'яткою №2 передбачає сформованість таких умінь, як уміння складати короткий запис задачі та уміння проводити аналітичний пошук розв'язання задачі, записувати розв'язок після слова “Розв'язання”, записувати словами відповідь після слова “Відповідь”.
Введення нового порядку в роботі над простими задачами повинно здійснюватися поступово, тобто кожне нове уміння опрацьовується окремо – спочатку формуємо у дітей уміння складати короткий запис задачі. Учням пропонується: § Прочитати задачу. (У гаражі було 10 автомобілів, 2 автомобілі виїхало. Скільки автомобілів залишилося в гаражі?) Подумати, про що в ній розповідається. § Зробити схематичний малюнок задачі. Як показати, що в гаражі було 10 автомобілів? (Треба накреслити відрізок і дужкою позначити, що він означає 10 автомобілів.) Як показати, що 2 автомобілі виїхало? (Треба з цього відрізку вилучити частину і показати дужкою – 2 виїхало.) Покажіть дужкою, скільки автомобілів залишилося.
§ Показати опорну схему до задачі; виділити ключові слова, тобто слова, які визначають ситуацію про яку йде мова в задачі: що було спочатку, що відбулося і що сталося потім; в опорній схемі записати ключові слова і відповідні їм числові значення. § Пояснити, що означає кожне число.(За коротким записом.) § Розв'язати задачу.
Після розв'язання задачі учні повторюють запитання задачі і учитель пропонує такі запитання: § Що потрібно знати, щоб відповісти на запитання задачі?(Щоб відповісти на запитання задачі потрібно знати: скільки автомобілів було в гаражі (10) і скільки автомобілів виїхало (2)) § Скільки числових значень треба знати, щоб відповісти на запитання задачі? (Щоб відповісти на запитання задачі треба знати два числа: 10 та 2.) Таким чином, щоб відповісти на запитання задачі “Скільки автомобілів залишилося в гаражі?”, треба знати два числові значення: 1 – скільки автомобілів було в гаражі (10) и П – скільки автомобілів виїхало із гаража (2). Якою дією ми відповіли на запитання задачі? (Дією віднімання, тому що залишилося менше, ніж було). Таким чином, у подальшій роботі над задачами обов'язково обговорюємо з учнями 1 – 3 пункти пам'ятки: запитуємо, про що розповідається в задачі, складаємо короткий запис до задачі, за коротким записом пояснюємо числові дані задачі, а далі пояснюємо вибір арифметичної дії, записуємо розв'язок задачі і відповідь (пишімо слова “розв'язок”, “відповідь”).
Розглянемо задачу. У підготовчій групі дитячого садка було:
Купили ще 4 поливальниці і 3 відерця. Скільки стало відерець? Скільки стало поливальниць? Ця задача надає вчителеві можливість показати учням необхідність обирати два числові значення для відповіді на запитання задачі, тобто познайомити учнів з аналітичним пошуком розв'язання задачі: § Уважно розгляньте малюнок, що ви бачите? (Ми бачимо відерці та поливальниці.) Скільки відерець? Скільки поливальниць? (Відерець 7 штук, поливальниць 5 штук.) § Прочитайте речення, яке пояснює, що це за відерці та поливальниці. (У підготовчій групі дитячого садка було…) Продовжуйте речення. (У підготовчій групі дитячого садка було 7 відерець та 5 поливальниць.) § Прочитайте речення, яке розповідає, що сталося потім. (Купили ще 4 поливальниці і 3 відерця.) § Розкажіть про що розповідається в задачі? (В задачі розповідається про те, що було 7 відерець та 5 поливальниць, купили ще 4 поливальниці і 3 відерця.) Ілюструємо умову задачі на дошці:
§ Прочитайте, про що запитується в задачі. (Скільки стало відерець? Скільки стало поливальниць?) Що тут незвичайного? (В задачі два запитання.) Чи можна відразу відповісти на два запитання? (Ні, не можна.) Тому відповімо спочатку на перше запитання, а потім на друге запитання. § Яке перше запитання? (Скільки стало відерець?) § Ця задача цікава тим, що тут є чотири числові значення, а для відповіді на запитання треба два числових значення, тому слід спочатку обміркувати, які з них слід вибрати… Для відповіді на запитання “Скільки стало відерець?” слід взяти числа, які стосуються кількості відерець. § Що потрібно знати, для того щоб дізнатися “Скільки стало відерець?” (Для того, щоб відповісти на це запитання, треба знати скільки відерець було (7) та скільки відерець купили (3).) Проілюструємо це в таблиці (вставляємо картки з словами, цифрами та знаком арифметичної дії):
Якою дією відповімо на запитання задачі? (Дією додавання, тому що відерець стало більше.) Запишімо розв'язок. Повторіть друге запитання. (Скільки стало поливальниць?) Що потрібно знати, щоб на нього відповісти? – відповідайте за пам'яткою. (Потрібно знати два числових значення: 1 – скільки було поливальниць (5) та П – скільки купили поливальниць (4).) Проілюструємо це в таблиці (вставляємо картки з словами, цифрами та знаком арифметичної дії):
§ Якою арифметичною дією відповімо на запитання задачі? (Дією додавання, тому що поливальниць стало більше.)
Розглянемо задачу: У господарки було 13 морквин, 3 морквини вона віддала козеняті. Скільки морквин залишилося? § Про що розповідається в задачі? (В задачі розповідається про морквини: було 13 морквин, віддали 3 морквини; запитується, скільки залишилося морквин.) § Виділи ключові слова та склади короткий запис задачі. Які слова розкривають ситуацію, описану в задачі? (Було, віддали, залишилося) Запишімо їх. Чи відомо, скільки морквин було? (Було – 13 морквин.) Чи знаємо ми із умови задачі, скільки віддали морквин? (Знаємо, віддали – 3 морквини) Чи відомо, скільки морквин залишилося? (Ні не відомо, поставимо знак запитання – це є запитання задачі.) Було – 13 м. Віддали – 3 м. Залишилося -? § За коротким записом поясни числові дані задачі та запитання. Що позначає число 13? (Число 13 позначає, скільки було морквин.) Що позначає число 3? (Число 3 позначає скільки віддали морквин.) Яке запитання задачі? (Скільки залишилося морквин?) § Повтори запитання задачі. Що потрібно знати, щоб на нього відповісти? (Потрібно знати два числових значення: 1 – скільки було морквин (13) та П – скільки віддали морквин (3).) Якою арифметичною дією відповімо на запитання задачі? (На запитання задачі відповімо дією віднімання, тому що залишилося менше, ніж було.) Процес аналізу ілюструємо схемою:
§ Запиши розв'язок задачі. (Розв'язок: 13 – 3 = 10 (м.)) § Запиши відповідь. (Відповідь: 10 морквин залишилося.)
Починаючи з цієї задачі всі наступні задачі розв'язуються за пам'яткою №2: запитання учителя створюються на підставі пунктів пам'ятки, а учні слідкують за текстом пам'ятки. Внаслідок такої роботи можна очікувати, що здійсниться недовільне запам'ятовування тексту пам'ятки, без прикладання спеціальних зусиль з боку учнів. Схематичний малюнок до задачі складається в разі потреби в ньому або за вимогою учителя. Самостійна робота над задачею здійснюється також за пам'яткою №2 з безпосереднім використанням тексту пам'ятки.
Лишилося розглянути питання про узагальнення і систематизацію знань учнів про задачі перших п'ятьох видів. З метою узагальнення знань учнів про задачу та про перші п'ять видів простих задач, можна запропонувати завдання типу: 1. Уважно прослухайте тексти. Який з них є задачею?
§ Чому перший текст не є задачею? (В ньому нема питання.) § Чому другий текст є задачею? (В ньому є умова і запитання.) § Розкажіть умову задачі. Що нам відомо із умови задачі? Що означає число 9? Що означає число 3? Як називаються числа, дані в умові задачі? (Числові дані.) § Розкажіть запитання задачі? Що означає число, яке треба знайти в задачі? Як воно називається? (Шукане число.) § Розв'яжіть задачу за пам'яткою № 2. § Покажіть її опорну схему. § Якою арифметичною дією ми відповіли на запитання задачі? (Дією віднімання.) Чому? (Тому що залишилося менше, ніж було. Менше число ми знаходимо дією віднімання.) § Що ми знайшли в цій задачі дією віднімання? (Скільки залишилося.) Тобто остачу. Такі задачі називаються задачами на знаходження остачі. § Покажіть опорну схему задач на знаходження остачі. 2. Уважно прослухайте текст. Чи є він задачею?
§ Розкажи умову. Розкажи запитання. Чи є цей текст задачею? § Чому цей тест не є задачею: в ньому ж є і умова і запитання? (Ситуація, яка описується в цьому тексті не відповідає дійсності – лампочки не можна їсти!) 3. Уважно прослухайте текст. Чи є він задачею?
§ Розкажіть умову. Розкажіть запитання. Отже в цьому тексті є і умова і запитання. § Цей текст є задачею? Чому? (Тут умова не пов'язана з запитанням.) § Який висновок можна зробити? (Задача складається з умови і запитання. При чому запитання повинно бути пов'язаним з умовою.) 4. На автостоянці було 5 легкових машин і 4 вантажні машини. § Чи це задача? (Ні, тут немає запитання.) § Яким повинно бути запитання в задачі? (Запитання повинно бути пов'язаним з умовою.) § Поставте запитання яке пов'язано з даною умовою. (Скільки всього машин на автостоянці?) § Розкажіть задачу. Розв'яжіть її за пам'яткою № 2. § Яке ще запитання можна поставити до даної умови? (На скільки більше легкових машин, ніж вантажних? Або на скільки менше вантажних машин, ніж легкових?) § Розкажіть цю задачу. Розв'яжіть її за пам'яткою № 2. § Якою арифметичною дією ми відповіли на запитання першої задачі? § Якою арифметичною дією ми відповіли на запитання другої задачі? § Чому на запитання першої задачі ми відповіли дією додавання? (Тому що в ній запитувалося, скільки всього машин. Всього машин більше, ніж окремо легкових і окремо вантажних. А більше число знаходимо дією додавання.) § Покажіть опорну схему задач, яких треба дізнатися, скільки всього. § В математиці, додаючи число, що ми знаходимо? (Суму.) Що вимагається знайти в таких задачах? (В таких задачах вимагається знайти суму.) Ці задачі називаються задачами на знаходження суми. § Покажіть опорну схему задач на знаходження суми. § Чому на запитання другої задачі ми відповіли дією віднімання? (Тому, що вимагалося дізнатися “на скільки більше?” або “на скільки менше”. Щоб дізнатися на скільки одне число більше чи менше за інше число, треба від більшого числа відняти менше число.) § Покажіть опорну схему задач, в яких треба дізнатися “на скільки більше” або “на скільки менше”. § В цій задачі треба було порівняти два числа. Якою арифметичною дією ми про це дізналися? (Відніманням.) Що в математиці ми знаходимо віднімаючи числа? (Різницю.) Отже, ці задачі називаються задачами на різницеве порівняння. § Покажіть опорну схему задач на різницеве порівняння. 5. Розв'яжіть задачу: “У дівчинки 6 зошитів у клітинку, а у лінійку на 3 більше. Скільки зошитів у лінійку у дівчинки?”. § Це задача? Чому? § Розв'яжіть її за пам'яткою № 2. § Покажіть її опорну схему. § Яке число є шуканим в цій задачі? (Число, яке означає кількість зошитів у лінійку. Число, яке більше 6 на 3.) Отже в цій задачі ми число 6 збільшували на 3. Ця задача називається задачею на збільшення числа на кілька одиниць. § Покажіть опорну схему задач на збільшення числа на кілька одиниць. § Якою арифметичною дією ми відповіли на запитання задачі на збільшення числа на кілька одиниць? (Дією додавання.) Чому? (Тому що більше число ми знаходили дією додавання. На 3 більше – це означає стільки ж та ще 3; стільки ж та ще 3 знаходимо дією додавання.) § Змініть умову задачі так, щоб вона розв'язувалася дією віднімання. (Треба, щоб зошитів в лінійку було на 3 менше, ніж у клітинку.) § Розкажіть цю задачу. Розв'яжіть її за пам'яткою № 2. § Покажіть її опорну схему. § Яке число є шуканим в цій задачі? (Число, яке на 3 менше 6.) Такі задачі називаються задачами на зменшення числа на кілька одиниць. § Покажіть опорну схему задач на зменшення числа на кілька одиниць. 6. На дитячому майданчику гралися 9 діточок. Серед них було 7 хлопчиків, а решта дівчинок. Скільки дівчинок було на дитячому майданчику? § Це задача? Чому? § Розв'яжіть задачу за пам'яткою № 2. § Покажіть опорну схему цієї задачі. § Що означає число 9? (Скільки всього дітей на майданчику.) Всього дітей більше чи менше, ніж окремо хлопчиків? Окремо дівчинок? § З кого “складаються” усі діти на майданчику? (Усі діти – це дівчинки і хлопчики. Всі діти = дівчинки + хлопчики.) Як на мові математиці називається число, яке отримується в результаті додаванн
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 728; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.100 (0.016 с.) |














 присунути
присунути

 Об'єднати змішати
зсипати
Коли додаємо стає більше.
сума
5 + 3 = 8
перший другий значення
доданок доданок суми
Об'єднати змішати
зсипати
Коли додаємо стає більше.
сума
5 + 3 = 8
перший другий значення
доданок доданок суми
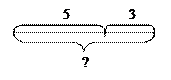 Сума складається з доданків.
Взаємозв'язок дій додавання і віднімання
Якщо від суми двох чисел відняти один доданок, то залишиться інший доданок.
Правило знаходження невідомого доданка
Щоб знайти невідомий доданок, треба від суми відняти відомий.
Переставний закон додавання
Від перестановки доданків значення суми не змінюється.
Сума складається з доданків.
Взаємозв'язок дій додавання і віднімання
Якщо від суми двох чисел відняти один доданок, то залишиться інший доданок.
Правило знаходження невідомого доданка
Щоб знайти невідомий доданок, треба від суми відняти відомий.
Переставний закон додавання
Від перестановки доданків значення суми не змінюється.
 відсунути
відсунути

 Вилучити відрізати
відсипати
Коли віднімаємо стає менше.
різниця
5 – 3 = 2
зменшуване від'ємник значення
різниці
Вилучити відрізати
відсипати
Коли віднімаємо стає менше.
різниця
5 – 3 = 2
зменшуване від'ємник значення
різниці
 Зменшуване складається з різниці та від'ємника.
Правило знаходження невідомого зменшуваного
Щоб знайти невідоме зменшуване, треба до різниці додати від'ємник.
Зменшуване складається з різниці та від'ємника.
Правило знаходження невідомого зменшуваного
Щоб знайти невідоме зменшуване, треба до різниці додати від'ємник.