Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пряма лінія, промінь, відрізокСодержание книги
Поиск на нашем сайте
Многокутники
Після повторення знань, результати якого знайшли утілення у таблиці, учням можна запропонувати завдання: 1. Порівняйте пряму лінію та промінь. Що в них спільного чим вони відрізняються? 2. Порівняйте пряму лінію та відрізок. Що в них спільного чим вони відрізняються? 3. Порівняйте промінь та відрізок. Що в них спільного чим вони відрізняються? 4. Скільки прямих ліній можна провести через одну точку? Скільки прямих ліній можна провести через дві відмінні точки? 5. Порівняйте назви многокутників з числом у них кутів, вершин та сторін. Що цікавого ви помітили? 6. Як би ви назвали многокутник, який має вісім кутів, вісім вершин і вісім сторін? 7. Складіть многокутник з семи лічильних паличок. Як ви його назвали? 8. Складіть дев'ятикутник з лічильних паличок. Скільки треба взяти паличок? 9. На які многокутники розбито фігуру?
Отже ми розглянули можливі лінії узагальнення і систематизації знань учнів з елементів геометрії за перший клас. Величини В першому класі діти познайомилися з величинами: довжиною, масою та об'ємом. Під час узагальнення і систематизації знань учні повинні зрозуміти, що об'єкти навколишнього світу можна порівнювати за величиною – довжиною, масою та об'ємом. Є кілька способів порівняння предметів за величиною, самий примітивний з них на “око”, а більш точний – вимірюванням. При чому процес вимірювання усіх величин завжди однаковий – обирається еталон (одиниця вимірювання) і підраховується скільки разів еталон міститься у величині даного предмету. Еталон обирають люди, і тому еталони можуть бути у різних людей різними. Так одиниці довжини у росіян та у англійців та французів були різними. Це дуже було не зручно. Тому люди всього світу домовилися про єдині еталони вимірювання величин. Які величини ви знаєте? (Довжину, масу та об'єм.) Далі йде повторення знань про величини, в результаті якого заповнюється таблиця за горизонтальними лініями: Величини
Після повторення матеріалу, результати якого відображені у таблиці, учням можна запропонувати завдання: 1. Що таке величина? (Це властивість предметів оточуючого світу.) 2. Які величини ви знаєте? 3. Що спільного в усіх величин? (Усі величини можна вимірювати.) 4. В чому полягає процес вимірювання величин? 5. Які одиниці вимірювання довжини (маси, об'єму) ви знаєте? Як співвідносяться сантиметр і дециметр? 6. Замініть одні одиниці вимірювання довжини іншими: 14 см =... дм... см 1 дм 7 см =... см 7. Виміряйте довжини відрізків:
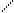
8. Накресліть відрізок, довжиною 6 см, 10 см, 11 см, 1дм 3 см. 9. На одну чашу терезів поклали гуску, а на другу чашу гирі 2 кг і 1 кг. Терези у рівновазі. Яка маса гуски? 10. На одну чашу терезів поклали цеглину і гирю 3 кг, а на другу гирі 2 кг і 3 кг. Яка маса цеглини? 11. У відро налили 8 літрових банок води. Відро стало повним. Який об'єм відра? 12. З повної каністри бензину відлили спочатку бензин у відро, об'ємом 8 літрів, а потім у дволітрову склянку, і каністра стала порожня. Який об'єм каністри? Таким чином, ми розглянули можливості узагальнення і систематизації знань учнів з питань про відомі їм величини, одиниці вимірювання величин та способи і процеси вимірювання величин. Методика вивчення нумерації Методика вивчення табличного додавання і віднімання Тема “Табличне додавання і віднімання двоцифрових чисел з переходом через десяток” вивчається в 2-му класі початкової школи. Під час вивчення теми учні повинні скласти таблиці і навчитися виконувати додавання і віднімання з переходом через десяток, застосовуючи для цього різні способи. Таким чином, мета вивчення даної теми полягає в формуванні у дітей обчислювальних навичок додавання і віднімання з переходом через десяток. Таблиці додавання і віднімання вивчаються не одночасно. Додаючи числа по частинах в межах 20, ми користуємося узагальненням, що числа можна додавати по частинах на підставі складу числа. Але при додаванні по частинах чисел 2,3,4,5 в межах 10, практично не має значення, яким випадком складу цих чисел користуватися, а при додаванні по частинах в межах 20 існує лише один варіант додавання чисел 3 – 9 по частинах, на підставі розкладання на зручні доданки, один із яких доповнює перший доданок суми до 10. Віднімаючи числа по частинах ми розкладаємо від'ємник на зручні доданки так, щоб один з них зменшував зменшуване до 10, тому що з 10 легко відняти кілька одиниць. Виходячи з цього на етапі актуалізації слід пропонувати учням: доповнювати (або зменшувати) числа до 10; згадати склад чисел: і випадки додавання і віднімання на підставі нумерації – на підставі десяткового складу числа; способи додавання і віднімання по частинах чисел першого п'ятка в межах 10. Перша таблиця, яку складають учні – це таблиця додавання числа 2. Тому, при складанні таблиці додавання числа 2, можна запропонувати таку бесіду: § Що означає до числа додати 2? (Це означає додати 1 та ще раз 1.) § Який новий випадок містить ця таблиця? (9 + 2) § Як ми до 9 додамо 2? (Так само, спочатку до 9 додамо 1, отримаємо 10, а потім до 10 додамо ще 1, отримаємо 11.) § Що цікавого ви помітили? (Ми спочатку додали до 9 одиницю і отримали число 10, а до 10 дуже просто додати ще 1 одиницю.) Аналогічно продовжується таблиця віднімання числа 2. При складанні таблиці додавання числа 3 пропонуємо запитання: § Які випадки складу числа 3 ви знаєте? (3 – це 2 і 1; 1 і 2.) § Скільки випадків складу числа 2 ви знаєте? (1) А складу числа 3? (2). § Чи можна додавати число 3 так само, як і число 2: по частинах на підставі складу числа? (Можна, але тут є 2 випадки складу числа, тому можуть бути 2 варіанти додавання по частинах: спочатку 2, а потім 1; спочатку 1, а потім 2.) § За яким варіантом треба міркувати? Що цікавого ви помітили, додаючи число 2 до 9? (Ми спочатку отримали 10, а потім до 10 легко додали ще 1 одиницю). § Тому треба користуватися таким варіантом, щоб отримати спочатку 10, тому що до 10 легко додати ще кілька одиниць. § Уважно розгляньте таблицю додавання числа 3. Які нові випадки додавання тут є? (8 + 3 і 9 + 3) § Як ми будемо виконувати додавання? (По частинах) § Як треба міркувати, щоб до 8 додати 3? (Треба число 3 розкласти на зручні доданки: це 2 і 1. Тому що 2 доповнює 8 до 10, а до 10 легко додати кілька одиниць.) § Як треба міркувати, щоб до 9 додати 3? (Треба число 3 розкласти на зручні доданки: це 1 і 2, тому що 1 доповнює 9 до 10, а до 10 легко додати кілька одиниць.) § Який висновок можна зробити додаючи числа по частинах? (Треба другий доданок розкласти на зручні доданки, потім доповнити перше число до 10, а потім до 10 додати решту одиниць.) Аналогічно розглядається складання таблиці віднімання числа 3 по частинах. Після вивчення таблиць додавання і віднімання чисел 2 і 3 нам здається можливим узагальнити способи додавання і віднімання по частинах, і перенести його на випадки додавання і віднімання чисел 4 та 5. Розгляньте приклади і зробити узагальнений висновок:
§ Що спільного в розв'язанні цих прикладів? (В усіх прикладах числа додаються по частинах. Другий доданок весь час замінюється сумою зручних доданків, так щоб один з них доповнював перше число до 10, а потім до 10 легко додати будь-яке число.) § Чи можна так само міркувати, щоб додати до 7 число 4?
§ А як треба міркувати, що до 8 додати 4?
§ А як треба міркувати, що до 9 додати 4?
§ Чим схожі всі ці приклади? Чим відрізняються? Чи є спільне в способі розв'язання? Чим відрізняються розв'язання? § Який висновок можна зробити? (Не має значення, яке число додають по частинах: його треба подати у вигляді суми зручних доданків, доповнити перше число до 10, а до десяти додати решту одиниць.) Аналогічно складається таблиці віднімання числа 4 та додавання і віднімання числа 5. З учнями можна скласти узагальнену пам'ятку:
З метою формування обчислювальних навичок додавання і віднімання чисел 2, 3, 4, 5 по частинах пропонуємо учням картки з друкованою основою:
Після такої роботи можна пропонувати учням самостійно виконувати розгорнений запис розв'язання. І лише після цього, дія додавання і віднімання по частинах може скорочуватися, а значить і запис розв'язку скорочується, і коли учень відразу може записати результат – розгорнений запис не виконується. Таким чином, уміння додавати і віднімати по частинах числа 2, 3, 4, 5 у дітей сформоване, і тому можна його перенести на випадки додавання і віднімання чисел 6, 7, 8, 9. Складаючи таблицю додавання числа 6,розглядаємо перший новий приклад 5 + 6. На підставі переставної властивості і висновку: “Зручніше до більшого числа додавати менше, треба поміняти місцями доданки.”,
§ Чи можна так само міркувати, щоб до 6 додати 6?
§ Таким чином, число 6 також можна додавати по частинах. Згадаємо, як треба міркувати, щоб додавати числа по частинах? Аналогічно складається вся таблиця додавання числа 6. Розглянемо, як можна перенести спосіб віднімання по частинах на випадки віднімання числа 6: Згадаємо, як 11 відняти 5.
§ Чи можна так само міркувати, щоб від 11 відняти 6?
§ Таким чином, число 6 також можна віднімати по частинах. § Чи можна так само міркувати при додаванні і відніманні чисел 7, 8, 9? Як треба міркувати. З метою формування обчислювальних навичок додавання і віднімання по частинах пропонуємо картки з друкованою основою:
Таким чином, ми розглянули складання таблиць додавання і віднімання способом додавання і віднімання по частинах. Але при складанні таблиць додавання виникає необхідність користуватися переставною властивістю дії додавання. З цим способом додавання учні познайомилися в межах 10, і тому його слід перенести в нову ситуацію: § Як треба міркувати, щоб до 2 додати 6?
2 + 6 = 6 + 2 = 8 § Чи можна так само міркувати, щоб до 4 додати 9?
4 + 9 = 9 + 4 = 13 § Як треба міркувати, щоб до 6 додати 8?
6 + 8 = 8 + 6 = 14
Одним із способів віднімання в межах 20 є віднімання на підставі взаємозв'язку між додаванням і відніманням. Цей спосіб не є новим, учні так віднімали числа другого п'ятка в межах 10, тому треба перенести це уміння в нову ситуацію. § Як треба міркувати, щоб від 9 відняти 7?
§ Чи можна так само міркувати, щоб від 11 відняти 7?
§ Як треба міркувати, щоб від 11 відняти 6?
§ Як треба міркувати в усіх випадках віднімання таким способом: на підставі взаємозв'язку між діями додавання і віднімання?
При відніманні на підставі взаємозв'язку між діями додавання і віднімання можна міркувати трохи інакше: з 12 відняти 7 – це означає знайти таке число, яке в сумі з від'ємником дає зменшуване: 12 – 6 = 6, тому що 6 + 6 = 12
6 + 6 З метою формування обчислювальних навичок учням можна пропонувати такі картки з друкованою основою:
+
+ Після того, як учні навчилися віднімати числа з переходом через десяток і по частинах і на підставі взаємозв'язку між додаванням і віднімання, пропонуємо їм обчислювати різниці двома способами:
+
+ +
+ Після складання таблиці віднімання числа 4 передбачено ознайомлення учнів з новим способом віднімання, який ми умовно назвали – порозрядне віднімання з переходом через розряд. На етапі актуалізації опорних знань треба повторити уміння замінювати двоцифрове число сумою розрядних доданків: 17 = 10 + 7 12 = 10 + 2 З метою мотивації введення нового способу обчислення, учням пропонується знайти різницю чисел міркуючи двома способами: 11 – 8 14 – 5 § Чим цікаві ці різниці? (В них зменшуване двоцифрове число). § А будь-яке двоцифрове число можна подати у вигляді суми розрядних доданків. Чи можна це застосувати при обчисленні різниць? § Як можна міркувати? (Число 11 – це 10 + 1.) Треба відняти 8; з якого числа будемо віднімати 8: з 1 чи з 10? (З одного не можна відняти 8, тому будемо віднімати 8 з 10, отримаємо 2.) І до отриманого результату 2 додамо решту одиниць:
10 + 1 § Чи отримали ми такий самий результат? § Як треба міркувати, щоб із 14 відняти 5?
10 + 4 § Взагалі, як треба міркувати, виконуючи віднімання таким способом?
З метою формування обчислювального навичка порозрядного віднімання пропонуємо учням для самостійної роботи картки:
Після цього можна картки трохи ускладнити:
Таким чином, учні познайомилися з трьома способами віднімання: по частинах, на підставі взаємозв'язку між додаванням і відніманням і порозрядне віднімання. У підручнику є вправи, в яких вимагається обчислити різницю трьома способами. Тому, пропонуємо учням і картки, в яких треба обчислити різницю трьома способами:
Отже, нами розглянуто способи складання таблиць додавання і віднімання з переходом через десяток. Треба зазначити, що якщо учні добре підготовлені, з високою навчаємося, то їх можна познайомити з способом округлення:
Таким чином, нами запропоновано методику складання таблиць з переходом через десяток і формування обчислювальних навичок додавання і віднімання в межах 20. Методика вивчення нумерації чисел В результаті вивчення теми діти повинні оволодіти наступними знаннями уміннями і навичками: 1. Знати назви чисел від 1 до 100 і порядок їх прямування при рахунку, місце кожного числа в ряду натуральних чисел. Вміти назвати сусідів будь-якого з даних чисел, в тому числі користуючись термінами “наступне”, “попереднє”. 2. Вміти утворювати числа з кількох десятків і кількох одиниць; встановлювати скільки десятків і скільки одиниць містить число. 3. Вміти утворювати числа способом прирахування та відрахування по одиниці. 4. Вміти записувати числа и читати записані числа. 5. Вміти порівнювати числа на підставі порядку прямування їх в натуральному ряді та на підставі десяткового складу чисел. 6. Навчитися виконувати додавання і віднімання виду: 54 + 1, 54 – 1 – на підставі знання порядку прямування чисел в натуральному ряді, 50 + 4, 54 – 4, 54 – 50 – на підставі знання десяткового складу чисел; уміти заміняти число сумою десятків та одиниць: 45 = 40 + 5.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.157.203 (0.009 с.) |

 пряму лінію.
пряму лінію.

 відрізок
відрізок





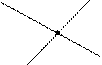

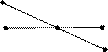







 1 дм – довжина відрізку, довжиною 10 см.
10 см = 1 дм
1 дм – довжина відрізку, довжиною 10 см.
10 см = 1 дм




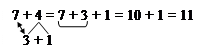
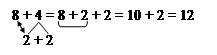

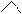






 отримуємо: 5 + 6 = 6 + 5, і згадуємо, як ми додавали число 5 по частинах:
отримуємо: 5 + 6 = 6 + 5, і згадуємо, як ми додавали число 5 по частинах: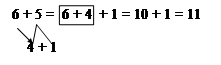
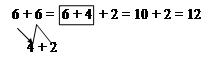
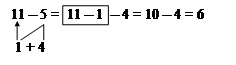
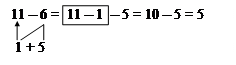
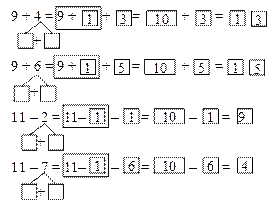







 17 – 8 =, т.щ. + =
17 – 8 =, т.щ. + = 12 – 3 =, т.щ. + =
12 – 3 =, т.щ. + =
 11 – 8 = 10 + 1 – 8 = 2 + 1 = 3
11 – 8 = 10 + 1 – 8 = 2 + 1 = 3 14 – 5 = 10 + 4 – 5 = 5 + 4 = 9
14 – 5 = 10 + 4 – 5 = 5 + 4 = 9