Методика введення поняття про обернену задачу

На прикладі порівняння задачі на знаходження суми і задачі на знаходження невідомого доданка вводиться поняття про обернену задачу. Це можна зробити наступним чином:

1. Каструля містить 5 л води, а бідон 3 л. Скільки літрів води містять разом каструля і бідон?

5 + 3 = 8 (л)

2. Каструля і бідон разом містять 8 л води. Каструля містить 5 л води. Скільки літрів води містить бідон?

8 – 5 = 3 (л)

§ Чим схожі ці задачі і чим вони відрізняються?

§ Як склали другу задачу з першої?

§ Друга задача обернена до першої. Склади ще одну задачу, яка обернена до першої.

Відповідаючи на запитання “Що спільного і відмінного в цих задачах?”, учні повинні зазначити, що спільним є те, що в обох задачах йде мова про одну й ту саму ситуацію: є каструля і бідон, в них налита вода; а відмінним є те, що в першій задачі відомо скільки літрів води вміщує каструля і скільки бідон і запитується скільки всього літрів води вміщують разом каструля і бідон, а в другій задачі також відомо скільки літрів води вміщує каструля, але невідомо скільки літрів води вміщує бідон, між тим сказано скільки літрів води всього в каструлі і в бідоні разом.

Тут корисно виписати числа задачі і пояснити, що означає кожне число: 5, 3, 8. А потім невідоме число, і першої і другої задачі, закрити знаком запитання і сформулювати задачі. А потім запитати “Яке ще число можна закрити знаком запитання?” і запропонувати скласти задачу, в якій запитується про це значення. Таким чином, ми розкриваємо учням технологію складання взаємо обернених задач:

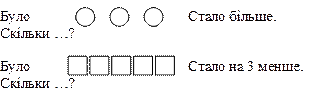
Після цього можна обговорити питання про те, чим цікаві ці три задачі: в них йде мова про одну й ту саму ситуацію, і в них дані однакові числа, але те, що було відомим в попередній задачі стало невідомим в наступній і навпаки. Відповідаючи на запитання “Як утворили другу задачу з першої?”, учні повинні сказати, що те що було невідомим в першій задачі (загальна кількість літрів води в каструлі і бідоні разом) стало відомим в другій задачі, а те що було відомим в першій задачі (кількість літрів води в бідоні) стало невідомим в другій. Учитель повідомляє, що такі задачі називаються оберненими.

Таким чином, щоб скласти обернену задачу, слід виписати числа задачі, пояснити їх і припустити, що одне із даних в умові задачі чисел є невідомим; і скласти задачу в якій запитується, про це число. Взагалі, обернених задач може бути стільки, скільки числових даних є в задачі. Учні складають ще одну обернену задачу:

3. Каструля і бідон разом містять 8 л води. Бідон містить 3 л води. Скільки літрів води містить каструля?

8 – 3= 5 (л)

Отже, тепер учні до кожної простої задачі повинні самостійно складати по дві обернені задачі. Розв'язок обернених задач розглядається, як перевірка вірності розв'язання задачі.

Методика формування поняття
про складену задачу

В темі “Табличне додавання і віднімання з переходом через десяток” учні знайомляться з поняттям про складену задачу. Ознайомленню з цим поняттям повинна передувати ґрунтовна підготовча робота.

1. Зміст і методика підготовчої роботи
до введення поняття “складена задача”

На ступені підготовчої роботи до формування поняття про складену задачу треба сформувати у дітей уявлення про те, що:

- до однієї умови можна поставити кілька запитань;

- одним і тим самим виразом можна розв'язати кілька задач;

- для відповіді на запитання задачі треба обирати числові дані, і може статися що потрібного числового значення не дістає;

- не завжди можна відповісти на запитання задачі однією арифметичною дією;

- існують такі задачі, які можна скласти з двох простих задач.

Таким чином, на ступені підготовчої роботи розв'язуються такі види завдань:

1) постановка запитання до даної умови;

2) складання задач з даними числами або числовими виразами;

3) задачі з числовими даними, яких не дістає;

4) задачі з двома пов'язаними запитаннями;

5) задачі з зайвими числовими даними;

6) дві послідовні прості задачі.

Розглянемо докладно кожний з визначених видів завдань.

1. Постановка запитання до даної умови

Засобом цих завдань у дітей формується уміння вірно оцінювати на яке запитання можна відповісти виходячи із певних даних, яке є важливим у наступній роботі над складеною задачею.

Н.Б. Істоміна пропонує починаючи з початкових етапів ознайомлення з поняттям “задача” систематично давати завдання на постановку запитання до умови, яка виражена незвичайно, наприклад:

Можна пропонувати ще такі завдання, наприклад:

Завдання 1. В гаражі було 11 машин. 8 машин поїхало.

Методика роботи над завданням:

Це задача? Чому? Як треба доповнити текст, щоб отримати задачу? Яким повинно бути запитання?

§ Розкажіть задачу з цим запитанням. Покажіть її опорну схему.

§ Визначить числові дані задачі та поясніть їх значення.

§

§ Повторіть запитання задачі. Що треба знати щоб на нього відповісти? (Треба знати два числові значення: 1 -... та П -...)

§ Якою арифметичною дією відповімо на запитання задачі? Чому?

§ Розкажіть розв’язання задачі.

Повторіть запитання задачі. Розкажіть відповідь.

Завдання 2. В каструлі 5 л молока, а в бідоні 9 л молока.

Методика роботи над аналогічними завданнями:

§ Виділіть числові дані. Про що можна дізнатися за цими числовими даними? Складіть задачу, в якій це число буде шуканим.

§ Про що ще можна дізнатися за цими числовими даними. Розкажіть задачу, в якій це число буде шуканим.