Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чисельні методи. Застосування. Основні принципи побудови.Содержание книги
Поиск на нашем сайте
Теоретичні відомості. Чисельні методи. Застосування. Основні принципи побудови. Чисельні методи — методи наближеного або точного розв'язування задач чистої або прикладної математики, які ґрунтуються на побудові послідовності дій над скінченною множиною чисел. Основні вимоги до чисельних методів, щоб вони були стійкими та збіжними. Чисельні методи називаються стійкими, якщо результати неперервно залежать від вхідних даних задачі або якщо похибка округлення, пов'язана з реалізацією чисельних методів на ЕОМ, залишається обмеженою при заданих межах зміни параметрів чисельних методів. Чисельні методи називаються збіжними, якщо результати прямують до точного розв'язання задачі при прямуванні параметрів чисельних методів до певних граничних значень. Основне питання теорії чисельних методів: отримання чисельних методів, які задовольняють вимогам високої точності, стійкості та економічності. Складання чисельних методів, що задовольняють цим вимогам, представляє собою складну задачу оптимізації чисельних методів. Статистична обробка експериментальних даних зазвичай ґрунтується на граничних теоремах теорії ймовірностей та вимагає обчислення оцінок в порівнянні з простими формулами. Однак для підвищення якості оцінок необхідна велика кількість даних, і обсяг обчислень може виявитися дуже великим. Тому чисельні методи тут націлені на скорочення обсягу обчислень при збереженні якості результатів. Найбільш ефективними чисельними методами в цій області відносяться методи, які застосовують швидке перетворення Фур'є. Для розв'язань задач апроксимації та обчислення функцій різних класів застосовують чисельні методи інтерполювання, найменших квадратів, ортогоналізації, врівноваження значень, умовної мінімізації та ін. Найбільш актуальним є методи кусково многочленної та раціональної сплайнової апроксимації, а також адаптивної апроксимації та нелінійної за параметром апроксимації. Чисельне інтегрування та диференціювання відбувається із означення відповідних операцій, однак з урахуванням необхідності економії обсягу обчислень та з урахування некоректності задачі диференціювання з'являється велика кількість чисельних методів для різних класів функцій та різного роду вихідних даних.
Основою чисельних методів розв'язання багатьох класів рівнянь є дискретизація задачі з наступним зведенням отриманих, загалом кажучи, нелінійні рівняння до послідовності систем алгебраїчних рівнянь. В зв'язку з цим чисельні методи можна поділити за способом дискретизації на проекційні, скінченно-різницеві та проекційно-різницеві, а за способом розв'язання лінійної системи — на прямі методи, ітераційні методи та комбіновані. Розв'язання різних класів рівнянь та багатьох інших задач зводяться до задач мінімізації функцій та функціоналів за наявності або відсутності обмежень. Чисельні методи розв'язання задач мінімізації випливають із різних ідей швидкого спуску по поверхні, яка відповідає мінімізованій функції. Сюди відносяться методи швидкого спуску, градієнтного, загального градієнтного та найшвидкішого спуску, методу можливих та спряжених напрямів і т. д.
Метод половинного ділення Метод половинного ділення – це найпростіший метод уточнення кореня рівняння. Він сходиться для будь-яких неперервних функцій
Алгоритм методу 1) На відрізку
2) Перевіряємо чи 3) У випадку, коли 4) Процес ділення відрізка навпіл виконується доти, поки на якомусь етапі, або середина відрізка буде коренем, або буде виконана умова закінчення ітераційного процесу: 5) У цьому випадку за наближене значення кореня вибирають 6) Вивід результатів. Кінець алгоритму. 7) Відомо, що при цьому похибка не перевищує Схема алгоритму розв'язання нелінійного рівняння методом половинного ділення представлена на рисунку 1.2.2.
Рисунок 1.2.2. – Схема алгоритму розв'язання нелінійного рівняння методом половинного ділення
Метод хорд. · Метод хорд є одним з найбільш поширених методів розв’язання алгебраїчних і трансцендентних рівнянь. В літературі він також зустрічається під назвою "метод лінійного інтерполювання" і "метод пропорційних частин". · Постановка задачі · Розглянемо рівняння · Суть методу хорд полягає в тому, що на достатньо малому відрізку
Рисунок 1.2.3. – Графічна інтерпретація методу хорд і процедури визначення рухомого кінця хорди Рівняння хорди, яка проходить через точки має вигляд
Знайдемо значення
Ця формула називається формулою методу хорд. Тепер корінь
Аналогічна для всякого
Процес стягування хордою продовжується багаторазово доти, поки не одержано наближений корінь із заданим степенем точності
де Слід відмітити, що розглянутий випадок (рис.1.2.3.а) перетину функції
Для автоматизації цього алгоритму необхідно розробити правило для автоматичного вибору рухомого кінця хорди і відповідно формули для обчислення наближеного значення кореня. Існує два правила визначення рухомого кінця хорди. Комбінований метод. Методи хорд і дотичних дають наближення кореня з різних сторін відрізку Постановка задачі Нехай дано рівняння Використаємо комбінований метод хорд і дотичних з урахуванням поведінки функції на відрізку
Рисунок 1.2.4. – Геометричний зміст комбінованого методу. методом дотичних – з недостачею (рис.1.2.4.в,г). Однак в усіх випадках справжній корінь Суть методу полягає в тому, що на досить малому відрізку
Наближене значення кореня нелінійного рівняння визначається відповідно до таких правил: Правило 1. Якщо добуток першої на другу похідну функції
Для методу дотичних рухомим є кінець
Правило 2. Якщо добуток першої на другу похідну функції
Для методу дотичних рухомим є кінець a, і наближене значення кореня обчислюється за формулою дотичних:
Комбінований метод дуже зручний при оцінці похибки обчислень. Ітераційний процес продовжується доти, поки не стане виконуватися нерівність Метод прямокутників. Найпростішим методом наближеного обчислення інтеграла є метод прямокутників, геометрична інтерпретація якого зводиться до знаходження визначеного інтеграла як суми площ N прямокутників (з висотою f(x) та основою h= Iпр=
Метод трапецій. Суть методу трапеції, полягає в тому, що інтеграл обчислюється по-іншому, відрізок інтегрування поділяється на N рівних відрізків, всередині яких підінтегральна крива f(x) замінюється кусково- лінійною функцією j(x), отриманою стягуванням ординат N відрізків хордами.
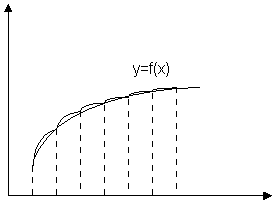
Рис.1.3.1. Метод парабол. Цей метод також використано у курсовій роботі, близький до методу трапецій у тій частині, що інтегрування проводиться шляхом поділу відрізка інтегрування [а, b] на множину відрізків (N пар відрізків). Однак, з метою збільшення точності наближеного інтегрування на кожному відрізку [Xi, Xi+2] підінтегральної функції f(x) замінюють квадратичною параболою j(x), обчислення визначеного інтеграла зводиться до обчислення суми N криволінійних трапецій Si: I=
Рисунок 1.3.2. Графічна модель.
Математичні вирази. До основних елементів математичних виразів MathCAD відносяться типи даних, оператори, функції і керуючі структури. Оператори - елементи MathCAD, за допомогою яких можна створювати математичні вирази. До них, наприклад, відносяться символи арифметичних операцій, знаки обчислення сум, добутків, похідної, інтегралу і т.д. Оператор визначає: 1. дію, що повинна виконуватися при наявності тих чи інших значень операндів; 2. скільки, де і які операнди повинні бути введені в оператор. Операнд – число чи вираз, на яке діє оператор. Наприклад, у виразі 5! + 3 число 3 і вираз 5! – операнди оператору + (плюс), а число 5 операнд оператору факторіал (!). Після вказівки операндів оператори стають блоками, що виконуються у документі. У Додатку 2 даного посібника наведено список операторів, що найбільш часто використовуються. Типи даних. До типів даних відносяться числові константи, звичайні і системні змінні, масиви (вектори і матриці) і дані файлового типу. Константами називають пойменовані об'єкти, що зберігають деякі значення, що не можуть бути змінені. Змінні є пойменованими об'єктами, що мають деяке значення, що може змінюватися по ходу виконання програми. Тип змінної визначається її значенням; змінні можуть бути числовими, рядковими, символьними і т.д. Імена констант, змінних і інших об'єктів називають ідентифікаторами. Ідентифікатори в MathCAD являють собою набір латинських чи грецьких букв і цифр. У MathCAD міститься невелика група особливих об'єктів, які не можна віднести ні до класу констант, ні до класу змінних, значення яких визначені одразу після запуску програми. Їх вірніше вважати системними змінними, що мають визначені системою початкові значення Зміну значень системних змінних роблять у вкладці Вбудовані змінні діалогового вікна Math Options команди Математика Þ Опції. Функція – вираз, відповідно до якого проводяться деякі обчислення з аргументами і визначається його числове значення. Слід особливо зазначити різницю між аргументами і параметрами функції. Змінні, зазначені в дужках після імені функції, є її аргументами і замінюються при обчисленні функції значеннями з дужок. Змінні в правій частині визначення функції, не зазначені дужках у лівій частині, є параметрами і повинні задаватися до визначення функції (див. Приклад 2 Малюнку 1).
Головною ознакою функції є повернення значення, тобто функція у відповідь на звернення до неї по імені з вказівкою її аргументів повинна повернути своє значення. Функції в пакеті MathCAD можуть бути вбудовані (див. Додаток 3), тобто завчасно введені розроблювачами, і визначені користувачем. Способи вставки вбудованої функції: 1. Вибрати пункт меню Вставка Þ Функція. 2. Натиснути комбінацію клавіш Ctrl + E. 3. Клацнути на кнопці функції.
Типи даних в Паскалі З точки зору програмування величини — це дані, якими оперує програма і які потребують місця в пам’яті комп’ютера. Залежно від формату представлення значень величини в пам’яті комп’ютера, множини допустимих значень, множини допустимих операцій величини поділяються на типи. Стандартні типи даних. Величини, значення яких зберігаються в одному елементі пам’яті, називають простими величинами. У Паскалі до них належать стандартні (базові) типи та їхні похідні: Опис величин. Для опису (оголошення) постійних величин використовується службове слово CONST, змінних — VAR. За допомогою оголошення встановлюється не тільки факт існування змінної, але і її тип. Приклад: VAR summer: integer; a1, b1: char; Структуровані типи даних. Це дані, що складаються з декількох елементів простого типу. Такі типи даних зручно використовувати, коли обробляється велика кількість даних одного типу або декілька даних різних типів об’єднуються в одну групу. До структурованих типів даних можна віднести рядки, масиви, записи, множини.
Чисельне інтегрування. Лістинг програми 1. uses crt; var h,s,a,x,b,e,suma:real; i,n:integer; function fun(var x:real):real; begin fun:=x/exp(1/2*ln(2+cos(pi*2))); end; begin clrscr; a:=0; b:=1.1; write('n='); readln(n); e:=0.0000001; suma:=0; repeat s:=suma; suma:=0; h:=(b-a)/n; x:=a+h/2; for i:=1 to n do begin suma:=suma+h*fun(x); x:=x+h; end; writeln('suma=',suma:14:12, ' n=', n:2, ' pogreshnost=', abs(s-suma):14:12); n:=n*2; until e>=abs(s-suma); writeln('suma=',suma:14:12, ' pogreshnost=', abs(s-suma):14:12, '<', e:10:7); readkey; end. Результат виконання.
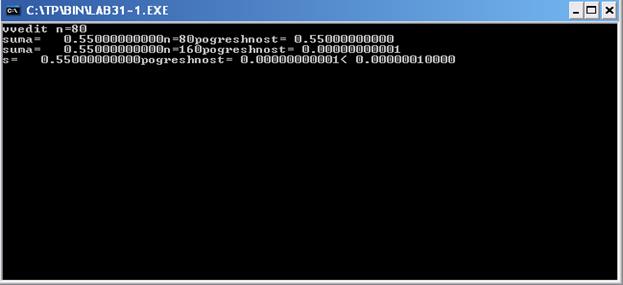
Лістинг програми 2. uses crt; var h,s,sk,a,x,b,e:real; i,n:longint; begin clrscr; a:=0; b:=1.1; write('vvedit n='); readln(n); e:=0.0000001; sk:=0; repeat s:=sk; sk:=0; h:=(b-a)/n; x:=a; for i:=1 to n do begin sk:=sk+(ln(1+h)/ln(1+h))*h/2; x:=x+h; end; writeln('suma=',sk:16:12, ' n=', n:2, ' pogreshnost=', abs(s-sk):14:12); n:=n*2; until e>=abs(s-sk); writeln('s=',sk:16:12, ' pogreshnost=', abs(s-sk):14:12, '<', e:14:12); readkey; end.
Результат виконання.
Лістинг програми 3. PROGRAM kyr;
USES CRT, Graph,VGL_Small; TYPE BaseType = real; Point = Record x, y: BaseType end; Index = 1..65520 div SizeOf (Point); PArrayPoint = ^ArrayPoint; ArrayPoint = array [Index] of Point; Clip = record Xmin:Integer; Ymin:Integer; Xmax:Integer; Ymax:integer; end; VAR nxmin, nxmax, nymin, nymax,a: Integer; ymin, ymax,xmin,xmax, pixx, pixy, tmin, tmax: real; ArrP,ArrTemp: PArrayPoint; ColPoint: Integer; gd,gm:integer; P:Clip; FUNCTION F1 (x: real): real; Begin F1:= x*cos(x); End;
FUNCTION F2 (t: real): real; Begin F2:= 2*arctan(t); End;
FUNCTION F3 (t: real): real; Begin F3:= 2*a*sqr(sin(t)); End; Function Gx(x:real):real; begin Gx:=x+(nxmax-nxmin) div 2+nxmin; end; Function Gy(y:real):real; Var Xasp,Yasp:word; begin GetAspectRatio(Xasp, Yasp); Gy:=(nymax-nymin) div 2 -(Xasp/Yasp)*y + nymin; end; Procedure LineClip(x1,y1,x2,y2:Integer); Const CodeBottom = 1; CodeTop = 2; CodeLeft = 4; CodeRight = 8; PROCEDURE Razm (var m, n, cp: Integer; pix: real); Begin m:= 1; n:= 0; If Round (m * Exp(n*Ln(10)) / pix) < 30 then While Round (m * Exp(n*Ln(10)) / pix) < 30 do begin Case m of 1: m:= 2; 2: m:= 5; 5: begin m:= 1; Inc (n) end end end Else begin While Round (m * Exp(n*Ln(10)) / pix) > 30 do begin Case m of 1: begin m:= 5; Dec (n) end; 2: m:= 1; 5: m:= 2; end end; Case m of 1: m:= 2; 2: m:= 5; 5: begin m:= 1; Inc (n) end end end; cp:= Round (m * Exp(n*Ln(10)) / pix) End;
PROCEDURE Out_CoordAxle; Var x, y, m, n, cp, ost, y1, x1, ch, i: Integer; mn: real; f: Boolean; Begin SetColor (GREEN); f:= true; if ymin >= 0 then y:= nymax else if ymax <= 0 then begin y:= nymin; f:= false; end else y:= nymax + Round (ymin/pixy); Line (nxmin, y, nxmax, y); Line (nxmax, y, nxmax-10, y+3); Line (nxmax, y, nxmax-10, y-3); if xmin >= 0 then x:= nxmin else if xmax <= 0 then x:= nxmax else x:= nxmin - Round (xmin/pixx); Line (x, nymin, x, nymax); if f then begin Line (x, nymin, x-3, nymin+10); Line (x, nymin, x+3, nymin+10); end; Razm (m, n, cp, pixx); ost:= abs (nxmin - x) mod cp; ch:= m * ((nxmin - x) div cp); SetTextJustify (centertext, toptext); if (nxmin - x) > 0 then begin ost:= cp - ost; Inc (ch, m) end; x1:= ost + nxmin; While x1 <= nxmax - 10 do begin Line (x1, y-3, x1, y+3); if ch <> 0 then OutTextXY (x1, y+10, MakeStr (ch)) else OutTextXY (x1 - 5, y+10, MakeStr (ch)); Inc (x1, cp); Inc (ch, m) end; if xmin > 0 then begin mn:= 1; for i:= 1 to Abs (n) do begin if n < 0 then mn:= mn * 10 else mn:= mn / 10 end; OutTextXY (nxmax-20, y+20, '(x+'+MakeStrR(xmin*mn, 2, 0)+')*10^'+MakeStr(n)) end else OutTextXY (nxmax, y+20, 'x*10^'+MakeStr(n)); Razm (m, n, cp, pixy); ost:= abs (-nymax + y) mod cp; ch:= m * ((-nymax + y) div cp); if (-nymax + y) > 0 then begin ost:= cp - ost; Inc (ch, m) end; y1:= nymax - ost; While y1 >= nymin+10 do begin Line (x-3, y1, x+3, y1); if ch <> 0 then OutTextXY (x-17, y1-3, MakeStr (ch)); Dec (y1, cp); Inc (ch, m); end; if ymin > 0 then OutTextXY (x, nymin-10, '(y+'+MakeStr(round(xmin))+')*10^'+MakeStr(n)) else OutTextXY (x, nymin-10, 'y*10^'+MakeStr(n)); SetColor (White) End;
var ch,ch1:char; k,h,d,t1,t2:real; i,j:integer; BEGIN ch:=#0; gd:=detect; { gm:=VgaHi;} initGraph(gd,gm,'c:\bp\bgi'); SetColor(Yellow); InitVgl; repeat ClearDevice; nxmin:= 50; nxmax:= 590; nymin:= 50; nymax:= 430; SetTextJustify (LeftText, TopText); SetColor(Yellow); OutTextXY(0,0,'1: Function given Obviously'); OutTextXY(0,20,'2: Function given in parameter'); OutTextXY(0,40,'3: Transformation of the diagrams'); OutTextXY(0,60,'Esc: Exit'); Ch:=readkey; case ch of '1': begin ClearDevice; SetColor(Yellow); Rectangle(nxmin-40, nymin-40, nxmax+40, nymax+40); xmin:= -pi; xmax:= 2*pi; MinMax1; SetColor (Red); Out_Wind; Out_CoordAxle; FreeMem (ArrP, Round ((nxmax-nxmin)) * Sizeof (Point)); OutTextXY(320,460,'Press any key'); ch:=readkey; ClearDevice; ch:=#0; end; '2': begin ClearDevice; SetColor(Yellow); Rectangle(nxmin-40, nymin-40, nxmax+40, nymax+40); tmin:= 0.01; tmax:= 10; a:=1; MinMax2; SetColor (Red); Out_Wind; Out_CoordAxle; FreeMem (ArrP, Round((nxmax-nxmin)) * Sizeof (Point)); OutTextXY(320,460,'Press any key'); ch:=readkey; ClearDevice; ch:=#0; end; '3': begin repeat nxmin:= 50; nxmax:= 450; nymin:= 50; nymax:= 430; P.xmin:= 50; P.xmax:= 450; P.ymin:= 50; P.ymax:= 430; ClearDevice; Rectangle(nxmin-40, nymin-40, nxmax+40, nymax+40); xmin:= -10; xmax:= 10; MinMax1; SetColor (Red); Out_Wind; Out_CoordAxle; SetTextJustify (LeftText, TopText); SetColor(Yellow); OutTextXY(500,0,'1: y=kx(x+h)+d'); OutTextXY(500,20,'2: y=F(|x|)'); OutTextXY(500,40,'3: y=|F(x)|'); OutTextXY(500,60,'4: y=|F(|x|)|'); ch1:=readkey; case ch1 of '1':begin OutTextXy(500,100,'k='); GotoXY(66,7);Read(k); SetFillStyle(0,0); Bar(500,90,600,110); OutTextXy(500,100,'h='); GotoXY(66,7);Read(h); Bar(500,90,600,110); OutTextXy(500,100,'d='); GotoXY(66,7);Read(d); Bar(500,90,600,110); vgl_pushmatrix; vgl_scale(1,k); vgl_translated(d,h); for i:=1 to (nxmax - nxmin) do begin arrp^[i].x:=XG(arrp^[i].x);arrp^[i].y:=YG(arrp^[i].y); Vgl_GetPoint(arrp^[i].x,arrp^[i].y); arrp^[i].x:=GX(arrp^[i].x);arrp^[i].y:=GY(arrp^[i].y); end; vgl_popmatrix; setcolor(green); Out_Wind1; ch1:=readkey; end; '2':begin vgl_pushmatrix; vgl_reflectionY; j:=0; for i:=(nxmax-nxmin) downto (nxmax-nxmin) div 2 do begin t1:=XG(arrp^[i].x);t2:=YG(arrp^[i].y); vgl_getPoint(t1,t2); t1:=Gx(t1);t2:=Gy(t2); arrp^[j+1].x:=t1; arrp^[j+1].y:=t2; j:=j+1; end; vgl_popmatrix; setcolor(green); Out_Wind; ch1:=readkey; end; '3':begin vgl_pushmatrix; vgl_reflectionX; for i:=1 to (nxmax - nxmin) do begin arrp^[i].x:=XG(arrp^[i].x);arrp^[i].y:=YG(arrp^[i].y); if arrp^[i].y<0 then VGL_GetPoint(arrp^[i].x,arrp^[i].y); arrp^[i].x:=GX(arrp^[i].x);arrp^[i].y:=GY(arrp^[i].y); end; vgl_popmatrix; setcolor(green); Out_Wind; ch1:=readkey; end; '4':begin vgl_pushmatrix; vgl_reflectionY; j:=0; for i:=(nxmax-nxmin) downto (nxmax-nxmin) div 2 do begin t1:=XG(arrp^[i].x);t2:=YG(arrp^[i].y); vgl_getPoint(t1,t2); t1:=Gx(t1);t2:=Gy(t2); arrp^[j+1].x:=t1; arrp^[j+1].y:=t2; j:=j+1; end; vgl_popmatrix; vgl_pushmatrix; vgl_reflectionX; for i:=1 to (nxmax - nxmin) do begin arrp^[i].x:=XG(arrp^[i].x);arrp^[i].y:=YG(arrp^[i].y); if arrp^[i].y<0 then VGL_GetPoint(arrp^[i].x,arrp^[i].y); arrp^[i].x:=GX(arrp^[i].x);arrp^[i].y:=GY(arrp^[i].y); end; vgl_popmatrix; setcolor(green); Out_Wind; ch1:=readkey; end; end; FreeMem (ArrP, Round ((nxmax-nxmin)) * Sizeof (Point)); until ch1=#27; end; end; Until ch=#27; CloseGraph;
END.
Результат виконання.
Висновки. Під час виконання розрахунокво-графічної роботи я досліджував методи половинного ділення, правий і лівих прямокутників, трапеції та інші. Кожен метод ефективний в залежності від виду функції. Я порівнював виконання цих методів у Excel та Pascal та звірив результати з Math Cad. Виконуючи завдання, я закріпив свої навички набуті протягом навчального року. Перелік літератури. 1. Е.А. Волков. Численные методы: Учеб. пособие для вузов. – М.: Наука, 1987.- 248с. 2. В.А. Ильина, П.К. Силаев. Численные методы для физиков-теоретиков. – Москва-Ижевск:ИКИ, 2003. – т 1,2. 3. Л.П. Фельдман, А.І. Петренко, О.А. Дмитрієва. Чисельні методи в інформатиці. – К.:Видавнича група BHV, 2006. - 480 c. 4. Н.Н. Калиткин Численные методы. М.: Наука, 1978. 5. Д. Каханер, К. Моулер, С.Неш. Численные методы и программное обеспечение. – М.:Мир, 2001. – 575с. 6. Березин И.С., Жидков Н.П. Методы вычислений. В 2–х т. М., 1959, т.1.– 464 с. т.2 – 602 с. 7. Н.С. Бахвалов, Н.П. Жидков, Кобельков Г.М. Численные методы: Учеб. пособие. - М.: Наука, 1987 – 600с. 8. И.А. Гулин, А.А. Самарский. Численные методы. М.: Наука, 1989. 9. Методы вычислений на ЭВМ: Справочное пособие/ Иванов В. В. — Киев: Наук. думка, 1986. — 564 с. 10. Р.Н.Кветний Методи комп’ютерних обчислень. Навчальний посібник.- Вінниця: ВДТУ, 2001.-148с. 11. www.posibnyky.vstu.vinnica.ua/chis_met/lek4.htm.
Теоретичні відомості. Чисельні методи. Застосування. Основні принципи побудови. Чисельні методи — методи наближеного або точного розв'язування задач чистої або прикладної математики, які ґрунтуються на побудові послідовності дій над скінченною множиною чисел. Основні вимоги до чисельних методів, щоб вони були стійкими та збіжними. Чисельні методи називаються стійкими, якщо результати неперервно залежать від вхідних даних задачі або якщо похибка округлення, пов'язана з реалізацією чисельних методів на ЕОМ, залишається обмеженою при заданих межах зміни параметрів чисельних методів. Чисельні методи називаються збіжними, якщо результати прямують до точного розв'язання задачі при прямуванні параметрів чисельних методів до певних граничних значень. Основне питання теорії чисельних методів: отримання чисельних методів, які задовольняють вимогам високої точності, стійкості та економічності. Складання чисельних методів, що задовольняють цим вимогам, представляє собою складну задачу оптимізації чисельних методів. Статистична обробка експериментальних даних зазвичай ґрунтується на граничних теоремах теорії ймовірностей та вимагає обчислення оцінок в порівнянні з простими формулами. Однак для підвищення якості оцінок необхідна велика кількість даних, і обсяг обчислень може виявитися дуже великим. Тому чисельні методи тут націлені на скорочення обсягу обчислень при збереженні якості результатів. Найбільш ефективними чисельними методами в цій області відносяться методи, які застосовують швидке перетворення Фур'є. Для розв'язань задач апроксимації та обчислення функцій різних класів застосовують чисельні методи інтерполювання, найменших квадратів, ортогоналізації, врівноваження значень, умовної мінімізації та ін. Найбільш актуальним є методи кусково многочленної та раціональної сплайнової апроксимації, а також адаптивної апроксимації та нелінійної за параметром апроксимації. Чисельне інтегрування та диференціювання відбувається із означення відповідних операцій, однак з урахуванням необхідності економії обсягу обчислень та з урахування некоректності задачі диференціювання з'являється велика кількість чисельних методів для різних класів функцій та різного роду вихідних даних. Основою чисельних методів розв'язання багатьох класів рівнянь є дискретизація задачі з наступним зведенням отриманих, загалом кажучи, нелінійні рівняння до послідовності систем алгебраїчних рівнянь. В зв'язку з цим чисельні методи можна поділити за способом дискретизації на проекційні, скінченно-різницеві та проекційно-різницеві, а за способом розв'язання лінійної системи — на прямі методи, ітераційні методи та комбіновані. Розв'язання різних класів рівнянь та багатьох інших задач зводяться до задач мінімізації функцій та функціоналів за наявності або відсутності обмежень. Чисельні методи розв'язання задач мінімізації випливають із різних ідей швидкого спуску по поверхні, яка відповідає мінімізованій функції. Сюди відносяться методи швидкого спуску, градієнтного, загального градієнтного та найшвидкішого спуску, методу можливих та спряжених напрямів і т. д.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 706; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.89.201 (0.017 с.) |

 , в тому числі недиференційованих. Швидкість сходження невелика
, в тому числі недиференційованих. Швидкість сходження невелика .
. вибираємо точку
вибираємо точку 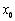 , яка розділяє його на два рівних відрізки
, яка розділяє його на два рівних відрізки 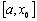 і
і 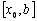 , довжина яких рівна і знаходиться за формулою
, довжина яких рівна і знаходиться за формулою
 , якщо так, то
, якщо так, то  , то з двох отриманих відрізків
, то з двох отриманих відрізків  вибираємо той, на кінцях якого функція
вибираємо той, на кінцях якого функція  , тоді залишаємо відрізок
, тоді залишаємо відрізок  переносимо в точку
переносимо в точку 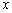 (
( ); якщо
); якщо  , то залишаємо відрізок
, то залишаємо відрізок  в точку
в точку  ) і переходимо до пункту 1.
) і переходимо до пункту 1. .
. .
. , де
, де  – число ітерацій.
– число ітерацій.
 , де
, де  (тобто
(тобто  ). Потрібно знайти наближене значення кореня
). Потрібно знайти наближене значення кореня  .
.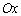 (рис.1.2.3.а).
(рис.1.2.3.а).

 , для якого
, для якого  , тобто для нерухомого кінця:
, тобто для нерухомого кінця:
 знаходиться всередині відрізка
знаходиться всередині відрізка  . Значення кореня
. Значення кореня  .
. -го наближення до точного значення кореня
-го наближення до точного значення кореня 

 – наближені значення коренів рівняння
– наближені значення коренів рівняння  -му ітераційному кроці;
-му ітераційному кроці; 

 `- з надлишком.
`- з надлишком. , (рис. 1.2.4.а, б) то рухомим для методу хорд є кінець a, і наближене значення кореня з боку кінця a обчислюється за формулою хорд:
, (рис. 1.2.4.а, б) то рухомим для методу хорд є кінець a, і наближене значення кореня з боку кінця a обчислюється за формулою хорд: .
. , і наближене значення кореня обчислюється за формулою дотичних:
, і наближене значення кореня обчислюється за формулою дотичних: .
. (рис. 1.2.4. в, г), то рухомим для методу хорд є кінець b, і наближене значення кореня з боку кінця b обчислюється за формулою хорд:
(рис. 1.2.4. в, г), то рухомим для методу хорд є кінець b, і наближене значення кореня з боку кінця b обчислюється за формулою хорд: .
. .
. . За наближене значення кореня приймають
. За наближене значення кореня приймають  , де
, де 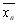 і
і  – наближені значення кореня відповідно з недостачею та з надлишком.
– наближені значення кореня відповідно з недостачею та з надлишком. xi=xi+1-xi), отриманих розділень відрізка[a,b] на N рівних частин, до того ж якщо розділити на прямокутники зліва на право, то отримаємо формулу лівих прямокутників:
xi=xi+1-xi), отриманих розділень відрізка[a,b] на N рівних частин, до того ж якщо розділити на прямокутники зліва на право, то отримаємо формулу лівих прямокутників:  f(x)dx»
f(x)dx»  Si=h[f(x0)+f(x1)+...+f(xn-1)]=
Si=h[f(x0)+f(x1)+...+f(xn-1)]= 
 f(xi);
f(xi);
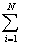 f(xi).
f(xi). (f(xi)+f(xi+1)).
(f(xi)+f(xi+1)). »
»  f(x0)+f(x1)+f(x2)+...+f(xn-1)+
f(x0)+f(x1)+f(x2)+...+f(xn-1)+  [
[  f(xi)].
f(xi)]. 
 Де М2 –максимальне значення другої похідної.f (x) при
Де М2 –максимальне значення другої похідної.f (x) при  h- крок обчислень.
h- крок обчислень.
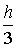 [f(xi)+4f(
[f(xi)+4f( xi+1)+f(xi+2)], тобто
xi+1)+f(xi+2)], тобто 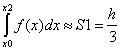 (y0+4y1+y2),
(y0+4y1+y2), 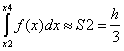 (y2+4y3+y4),
(y2+4y3+y4),  (y4+4y5+y6),
(y4+4y5+y6), 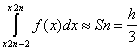 (y2n-2+4y2n-1+y2n),
(y2n-2+4y2n-1+y2n),  [y0+y2n+4(y1+...+y2n-1)+2(y2+...+y2n-2)],
[y0+y2n+4(y1+...+y2n-1)+2(y2+...+y2n-2)],