
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чисельне розв’язання трансцендентних рівнянь. Опис методів дихотомії (половинного ділення), хорд, дотичних, комбінованого методу хорд та дотичних
До трансцендентних функцій відносять всі неалгебраїчні функції: Показникові ах, логарифмічні Нелінійні рівняння, які містять трансцендентні функції називаються нелінійними трансцендентними рівняннями. Розв’язком нелінійного рівняння на ЕОМ називається вектор В нелінійному рівнянні виду
і -та координата вектора
Рисунок 1.2.1. – Графічна інтерпретація методу половинного ділення. Алгоритм методу (рис.1.2.1.) оснований на багатократному ділені навпіл і звужуванні досліджуваного відрізка
Метод половинного ділення Метод половинного ділення – це найпростіший метод уточнення кореня рівняння. Він сходиться для будь-яких неперервних функцій
Алгоритм методу 1) На відрізку
2) Перевіряємо чи 3) У випадку, коли 4) Процес ділення відрізка навпіл виконується доти, поки на якомусь етапі, або середина відрізка буде коренем, або буде виконана умова закінчення ітераційного процесу: 5) У цьому випадку за наближене значення кореня вибирають 6) Вивід результатів. Кінець алгоритму. 7) Відомо, що при цьому похибка не перевищує Схема алгоритму розв'язання нелінійного рівняння методом половинного ділення представлена на рисунку 1.2.2.
Рисунок 1.2.2. – Схема алгоритму розв'язання нелінійного рівняння методом половинного ділення
Метод хорд. · Метод хорд є одним з найбільш поширених методів розв’язання алгебраїчних і трансцендентних рівнянь. В літературі він також зустрічається під назвою "метод лінійного інтерполювання" і "метод пропорційних частин". · Постановка задачі · Розглянемо рівняння · Суть методу хорд полягає в тому, що на достатньо малому відрізку
Рисунок 1.2.3. – Графічна інтерпретація методу хорд і процедури визначення рухомого кінця хорди Рівняння хорди, яка проходить через точки має вигляд
Знайдемо значення
Ця формула називається формулою методу хорд. Тепер корінь
Аналогічна для всякого
Процес стягування хордою продовжується багаторазово доти, поки не одержано наближений корінь із заданим степенем точності
де Слід відмітити, що розглянутий випадок (рис.1.2.3.а) перетину функції
Для автоматизації цього алгоритму необхідно розробити правило для автоматичного вибору рухомого кінця хорди і відповідно формули для обчислення наближеного значення кореня. Існує два правила визначення рухомого кінця хорди.
Комбінований метод. Методи хорд і дотичних дають наближення кореня з різних сторін відрізку Постановка задачі Нехай дано рівняння Використаємо комбінований метод хорд і дотичних з урахуванням поведінки функції на відрізку
Рисунок 1.2.4. – Геометричний зміст комбінованого методу. методом дотичних – з недостачею (рис.1.2.4.в,г). Однак в усіх випадках справжній корінь Суть методу полягає в тому, що на досить малому відрізку Наближене значення кореня нелінійного рівняння визначається відповідно до таких правил: Правило 1. Якщо добуток першої на другу похідну функції
Для методу дотичних рухомим є кінець
Правило 2. Якщо добуток першої на другу похідну функції
Для методу дотичних рухомим є кінець a, і наближене значення кореня обчислюється за формулою дотичних:
Комбінований метод дуже зручний при оцінці похибки обчислень. Ітераційний процес продовжується доти, поки не стане виконуватися нерівність
|
||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.212 (0.027 с.) |
 ,
,  , тригонометричні sin x, cos x, tgx, ctgx, обернені тригонометричні
, тригонометричні sin x, cos x, tgx, ctgx, обернені тригонометричні  та інші.
та інші.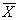 , координати якого
, координати якого  при підстановці в початкове рівняння перетворює його в тотожність.
при підстановці в початкове рівняння перетворює його в тотожність.
 називається і - тим коренем рівняння, а а1, а2, …, ат - коефіцієнтами рівняння. Нехай маємо рівняння
називається і - тим коренем рівняння, а а1, а2, …, ат - коефіцієнтами рівняння. Нехай маємо рівняння  , де
, де  – неперервна, монотонна нелінійна функція, яка має на відрізку
– неперервна, монотонна нелінійна функція, яка має на відрізку  єдиний корінь
єдиний корінь  , тобто добуток
, тобто добуток  , причому
, причому  , де
, де  – задана похибка обчислень. Потрібно знайти значення кореня
– задана похибка обчислень. Потрібно знайти значення кореня 
 .
.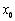 , яка розділяє його на два рівних відрізки
, яка розділяє його на два рівних відрізки 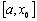 і
і 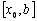 , довжина яких рівна і знаходиться за формулою
, довжина яких рівна і знаходиться за формулою
 , якщо так, то
, якщо так, то  , то з двох отриманих відрізків
, то з двох отриманих відрізків  вибираємо той, на кінцях якого функція
вибираємо той, на кінцях якого функція  , тоді залишаємо відрізок
, тоді залишаємо відрізок  переносимо в точку
переносимо в точку 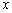 (
( ); якщо
); якщо  , то залишаємо відрізок
, то залишаємо відрізок  в точку
в точку  ) і переходимо до пункту 1.
) і переходимо до пункту 1. .
. .
. , де
, де  – число ітерацій.
– число ітерацій.
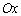 (рис.1.2.3.а).
(рис.1.2.3.а).

 , для якого
, для якого  , тобто для нерухомого кінця:
, тобто для нерухомого кінця:
 знаходиться всередині відрізка
знаходиться всередині відрізка  . Значення кореня
. Значення кореня  .
. -го наближення до точного значення кореня
-го наближення до точного значення кореня 

 – наближені значення коренів рівняння
– наближені значення коренів рівняння  -му ітераційному кроці;
-му ітераційному кроці; 

 `- з надлишком.
`- з надлишком. , (рис. 1.2.4.а, б) то рухомим для методу хорд є кінець a, і наближене значення кореня з боку кінця a обчислюється за формулою хорд:
, (рис. 1.2.4.а, б) то рухомим для методу хорд є кінець a, і наближене значення кореня з боку кінця a обчислюється за формулою хорд: .
. , і наближене значення кореня обчислюється за формулою дотичних:
, і наближене значення кореня обчислюється за формулою дотичних: .
. (рис. 1.2.4. в, г), то рухомим для методу хорд є кінець b, і наближене значення кореня з боку кінця b обчислюється за формулою хорд:
(рис. 1.2.4. в, г), то рухомим для методу хорд є кінець b, і наближене значення кореня з боку кінця b обчислюється за формулою хорд: .
. .
. . За наближене значення кореня приймають
. За наближене значення кореня приймають  , де
, де 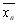 і
і  – наближені значення кореня відповідно з недостачею та з надлишком.
– наближені значення кореня відповідно з недостачею та з надлишком.


