Законы и тождества алгебры логики

Математический аппарат алгебры логики позволяет преобразовать логическое выражение, заменив его равносильным с целью упрощения, сокращения числа элементов или замены элементной базы.

Законы:

1 Переместительный: X ∨ Y = Y ∨ X; X · Y = Y · X.

2 Cочетательный: X ∨ Y ∨ Z = (X ∨ Y) ∨ Z = X ∨(Y ∨ Z); X · Y · Z = (X · Y) · Z = X· (Y· Z).

3 Идемпотентности: X ∨ X = X; X · X = X.

4 Распределительный: (X ∨ Y)· Z = X· Z ∨ Y· Z.

5 Двойное отрицание: .

6 Закон двойственности (Правило де Моргана):

Для преобразования структурных формул применяется ряд тождеств:

X ∨ X · Y = X; X(X ∨ Y) = X — Правила поглощения.

X· Y ∨ X· = X, (X ∨ Y)·(X ∨ ) = X – Правила склеивания.

Правила старшинства логических операций.

1 Отрицание — логическое действие первой ступени.

2 Конъюнкция — логическое действие второй ступени.

3 Дизъюнкция — логическое действие третьей ступени.

Если в логическом выражении встречаются действия различных ступеней, то сначала выполняются первой ступени, затем второй и только после этого третьей ступени. Всякое отклонение от этого порядка должно быть обозначено скобками.

 

Дослідження логічних функцій одного і двох змінних і їх реалізація; побудова простих пристроїв автоматики на базі логічних і цифро-імпульсних пристроїв.

Цифровые устройства комбинационного типа

Цифровыми устройствами комбинационного типа или цифровыми автоматами без памяти называются цифровые устройства, логические значения на выходе которых однозначно определяются совокупностью или комбинацией сигналов на входах в данный момент времени. К ним относятся суммирующие схемы, шифраторы и дешифраторы, мультиплексоры и демультиплексоры, цифровые компараторы и другие устройства. Цифровые устройства комбинационного типа выпускаются в виде интегральных микросхем или входят в состав больших интегральных микросхем, таких как процессоры, запоминающие и другие устройства.

Двоичные сумматоры

Одноразрядные сумматоры

В цифровой вычислительной технике используются одноразрядные суммирующие схемы с двумя и тремя входами, причём первые называются полусумматорами, а вторые — полными одноразрядными сумматорами. Полусумматоры могут использоваться только для суммирования младших разрядов чисел. Полные одноразрядные сумматоры имеют дополнительный третий вход, на который подаётся перенос из предыдущего разряда при суммировании многоразрядных чисел.

На рисунке 21, а) приведена таблица истинности полусумматора, на основании которой составлена его структурная формула в виде СДНФ (Рисунок 21, б). Функциональная схема, составленная на элементах основного базиса в соответствии с этой структурной формулой, приведена на рисунке 21, в).

Рисунок 21 Одноразрядный полусумматор: а) таблица истинности, б) структурная формула, в) функциональная схема.

 

Основными параметрами, характеризующими качественные показатели логических схем, являются быстродействие и количество элементов, определяющее сложность схемы.

Быстродействие определяется суммарным временем задержки сигнала при прохождении элементов схемы. В приведённой выше схеме быстродействие определяется задержкой в трёх логических элементах.

Кроме количества элементов сложность схемы, как было отмечено выше, определяется количеством входов элементов, по которым выполняются логические операции. Этот параметр называется «Число по Квайну». Приведённая выше схема содержит 6 элементов и имеет 10 входов (Число по Квайну равно 10).

Недостатком схемы рисунок 21, в) является то, что на её входы необходимо подавать и прямые и инверсные значения операндов. Применяя законы алгебры логики схему можно преобразовать, исключив инверсии над отдельными операндами. Порядок минимизации показан на рисунке 22, а), функциональная схема — на рисунке 22, б), а её УГО — на рисунке 22, в).

Рисунок 22 Пример минимизации а), функциональная схема б) и УГО одноразрядного полусумматора в).

 

Минимизированная схема является более быстродействующей, так как вместо 6 содержит 3 элемента, а число по Квайну уменьшилось с 10 до 7. Учитывая огромное количество используемых суммирующих схем, выигрыш можно считать весьма ощутимым.

Схему полного одноразрядного сумматора можно получить на основе двух схем полусумматоров и схемы «ИЛИ», как показано на рисунке 23,а).

Рисунок 23 Одноразрядный полный сумматор: а) — функциональная схема на двух полусумматорах; б) — УГО; в) — таблица истинности: г) — минимизированная схема.

 

Из рассмотрения принципа работы функциональной схемы рисунок 23,а) составлена её таблица истинности, анализ которой показывает, что данная схема выполняет функции полного одноразрядного сумматора. Однако схема не является оптимальной по быстродействию, поскольку в ней сигнал проходит последовательно через две схемы полусумматоров и схему ИЛИ.

Представляется целесообразным разработка сумматора как устройства, имеющего три входа и два выхода. СДНФ такой функции записывается в виде:

Минимизированные значения, используемые в интегральной схемотехнике:

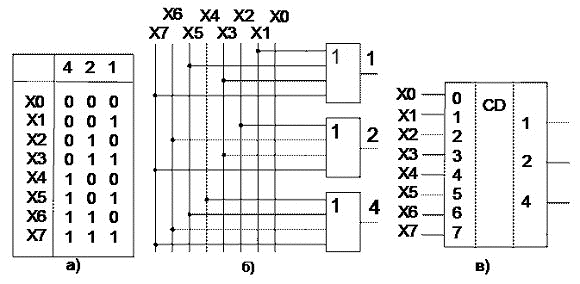
P_{I +1} = P_Ia + P_Ib + ab

Первое из уравнений минимизируется аналитическим методом, используя законы алгебры логики, а второе — методом минимизирующих карт Карно.

Функциональная схема, составленная по этим уравнениям, приведена на рисунке 23, г). По сравнению со схемой рисунок 23, а) эта схема является более быстродействующей. Условное графическое обозначение (УГО) схемы полного одноразрядного сумматора приведено на рисунке 23, б).

Кодирующие и декодирующие устройства

Шифраторы

Шифратор (кодер) — это функциональный узел, предназначенный для преобразования поступающих на его входы управляющих сигналов (команд) в n-разрядный двоичный код. В частности, такими сигналами или командами могут быть десятичные числа, например, номер команды, который с помощью шифратора преобразуется в двоичный код.

В качестве примера разработаем схему 3-разрядного шифратора. Вначале следует построить таблицу кодов (таблицу истинности), в которой код номера сигнала представим, например, двоичным кодом (Рисунок 27,а). Схема, реализованная на элементах ИЛИ, приведена на рисунке 27,б.

Рисунок 27 Таблица кодов 3-разрядного шифратора а), его функциональная схема б) и УГО в).

 

В общем случае, при использовании двоичного кода, можно закодировать 2ⁿ входных сигналов. В рассмотренной выше схеме выходной код «000» будет присутствовать на выходе при подаче сигнала на вход X0 и в случае, если входной сигнал вообще не подаётся ни на один из входов. Для однозначной идентификации сигнала X0 в интегральных схемах формируется ещё один выходной сигнал — признак подачи входного сигнала, который используется и для других целей.

Дешифраторы (декодеры)

Дешифратор — функциональный узел, вырабатывающий сигнал «лог. 1» (дешифратор высокого уровня) или сигнал «лог. 0» (дешифратор низкого уровня) только на одном из своих 2ⁿ выходах в зависимости от кода двоичного числа на n входах.

Рисунок 29 Дешифратор: а) – таблица истинности; б) – функциональная схема

 

Дешифраторы широко используются в устройствах управления, где они формируют управляющий сигнал в соответствии с входным кодом, который воздействует на какое-либо исполнительное устройство.