
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диз’юнктивні нормальні форми.Содержание книги
Поиск на нашем сайте Відомо, що: - головним завданням математики логіки є вивчення математичних законів; - існує простий універсальний метод (табличний), який дозволяє для будь-якої формули алгебри висловлень скінченним числом дій визначити чи є вона логічним законом; - таблиця істинності логічної формули дає повну, вичерпну картину значень істинності цієї формули. Якщо формула алгебри висловлень істинна хоча б на одному наборі, то вона називається здійсненною. Наприклад:
На наборі 1,0 формула набирає значення істинності, тому вона називається здійсненною. Якщо формула алгебри висловлень на кожному наборі хибна, то вона називається нездійсненною. За допомогою таблиць легко виявити характер логічної формули. Якщо останній рядок таблиці істинності формули: 1) містить хоча б одну одиницю, то ця формула здійсненна; 2) складається з одних одиниць, то вона завжди істинна (логічний закон) 3) складається лише з нулів, то вона тотожно хибна (нездійсненна) Логічний закон – це формула, яка істинна на будь-якому наборі.
До основних логічних законів належать: 1) Закон тотожності -
2) Закон суперечності -
3) Закон виключеного третього -
Табличний метод не такий ефективний на практиці, як в теорії, він надто громіздкий для складних формул. Тому для фактичного дослідження характеру істинності логічної формули застосовують більш зручні методи. Вони полягають у зведенні логічних формул тотожними перетвореннями до так званих нормальних форм. Логічну формулу називають попередньою формою, якщо вона має такі властивості: 1) містить тільки основні логічні операції: диз’юнкцію, кон`юнкцію і заперечення; 2) кожен знак заперечення стосується тільки основного висловлення (окремої букви). Приклади:
Теорема: Для кожної формули алгебри висловлень існує логічно рівна їй попередня форма, яку можна знайти за допомогою скінченного числа дій: - якщо над виразом стоїть кілька рисок заперечення, то їх можна відкинути, якщо їх число парне і залишити одну, якщо їх число не парне (це випливає із закону подвійного заперечення) - імплікацію або еквівалентність заміняють
Завдання: звести логічні формули до попередньої форми. 1/ 2/ 3/ 4) 5) 6) Логічний добуток кількох змінних, взятих із запереченням або без них називається елементарним добутком (кон`юнкцією). Зауваження: одна буква Приклади:
Теорема: Елементарний добуток дорівнює 1 на одному наборі, коли змінним із запереченням присвоєний нуль, а змінним без заперечення 1.
Логічна функція, яка подається диз’юнкцією (сумою) елементарних добутків називається диз’юнктивною нормальною формою (ДНФ). * ДНФ відносно висловлень 1) елементарний добуток 2) диз`юнкція різних елементарних добутків відносно 3) тотожна хибність Для кожної формули алгебри висловлень існує ДНФ, яка може бути знайдена за допомогою скінченого числа дій. Алгоритм з ведення логічної формули до ДНФ: 1) зводимо до трьох основних операцій: 2) якщо є добутки диз’юнкції, то застосовують
3) на підставі закону тавтології Після таких скорочень залишається або елементарний добуток Звести до ДНФ: а)
б) = в)
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |







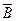

 (якщо Х, то Х)
(якщо Х, то Х)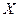

 (не можуть однозначно бути істинними
(не можуть однозначно бути істинними  )
)

 (з висловлень
(з висловлень 
 ;
; 
 - знак заперечення стосується складної формули;
- знак заперечення стосується складної формули; - не попередні форми, містить не основні операції.
- не попередні форми, містить не основні операції.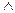 , тоді риски заперечення будуть стояти над окремими буквами або над диз’юнкцією або кон`юнкцією. В цьому випадку застосовують закони де Моргана і риски заперечення перейдуть на множники, або додатки.
, тоді риски заперечення будуть стояти над окремими буквами або над диз’юнкцією або кон`юнкцією. В цьому випадку застосовують закони де Моргана і риски заперечення перейдуть на множники, або додатки.







 не може зустрічатися в ньому більше одного разу.
не може зустрічатися в ньому більше одного разу. -елементарні добутки.
-елементарні добутки. - не є елементарними добутками.
- не є елементарними добутками.
 │
│ 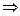
 │
│ 
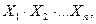 називається формула кожного з трьох типів:
називається формула кожного з трьох типів: .
. ¯;
¯; дистрибутивні закони:
дистрибутивні закони:
 викреслюємо повторні множники або зайві додатки, а також додатки типу
викреслюємо повторні множники або зайві додатки, а також додатки типу  (на основі закону суперечності).
(на основі закону суперечності).
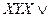








 =
=  =
= 

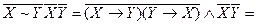


 - тотожна хибніст
- тотожна хибніст




