Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Досконала диз’юнктивна нормальна форма. (ДДНФ)Содержание книги
Поиск на нашем сайте
Конституентою одиниці основних висловлень Конституента одиниці відносно Всі множники конституенти одиниці позначаються різними буквами. Для двох висловлень Для трьох висловлень отримуємо вісім конституент одиниці:
Кожна конституента одиниці істинна на одному і тільки одному наборі. Між конституентами одиниці для - кожній конституенті одиниці відповідає єдиний набір на якому вона істинна; - кожен набір відповідає єдиній конституенті одиниці. Наприклад: 1)
2) Висновки: 1) число конституент одиниці відносно для для 2) якщо на якомусь наборі Конституенти одиниці для двох змінних: n=2.
Конституенти одиниці для трьох змінних: n=3.
Диз`юнктивна нормальна форма називається досконалою, якщо всі її доданки є конституентами одиниці. Теорема: Якщо формула алгебри висловлень здійсненна, то для неї існує ДДНФ і вона може бути знайдена за допомогою скінченного числа дій. Щоб отримати ДДНФ треба: - якщо в „неповний ” елементарний добуток не входить - розкривають дужки за першим дистрибутивним законом
- після цього повторні доданки видаляють. Приклад: Область істинності: здійсненої формули складається з наборів що відповідають конституентам одиниці, які входять в ДДНФ.
Область хибності знаходять виключивши з усіх можливих наборів область істинності.
Область істинності: 010;111;110;000;101. Область хибності: 011;100;001.
Скорочена ДНФ. ДДНФ є найбільш загальною формою подання логічних функцій в диз`юктивній нормальній формі і тому містить найбільш можливе число літер. Число літер, що входять до ДНФ логічної функції дорівнює або більше числа змінних, які містяться в цій функції оскільки одна і та сама змінна може входити до функції кілька разів. Наприклад: ДНФ(F)= Містить 6 літер (а змінних 3) внаслідок того, що А - входить до функції двічі, В -тричі. На практиці і відповідно в теорії постає проблема скорочення числа літер у ДДНФ. Імпліканта. Застосування терміну імпліканта пов’язане з логічною функцією F= Вираз
Якщо деяка логічна функція - будь-яка конституента одиниці, що входить до ДДНФ логічної функції F, є її імплікантою. - константа нуля є імплікантою будь-якої логічної функції. Доведення: Дійсно константа нуля („ F=0 ”) за означенням дорівнює 0 на всіх її можливих наборах і тому обов’язково дорівнює 0 на всіх тих наборах, на яких функція F дорівнює нулю. - будь-яка логічна функція є імплікантою самої себе. - будь-яка логічна функція є імплікантою константи одиниці. Скорочена ДНФ. Елементарний добуток, одержаний шляхом виключення з початкового добутку однієї або кількох змінних, називається власною частиною добутку. Приклад: Елементарні добутки, які входять до даної функції в ДДНФ, але ніяка їх власна частина самостійно, як добуток не входить, називаються простими імплікантами. Приклад: Нехай добутки
Прикладом такої функції буде
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 941; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.79.193 (0.009 с.) |

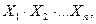 називається повний елементарний добуток, який містить усі букви
називається повний елементарний добуток, який містить усі букви  або
або  (тобто кожне з основних висловлень
(тобто кожне з основних висловлень 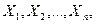 входить в цей добуток).
входить в цей добуток). і
і 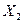 можна утворити чотири конституенти одиниці:
можна утворити чотири конституенти одиниці: 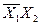 ,
, 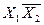 ,
, 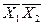 .
.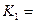
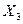 ;
;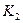 =
= 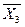 ;
; ;
; ;
;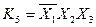 ;
; ;
;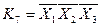 ;
;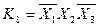

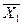
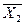

 дорівнює числу
дорівнює числу 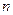 -місних наборів: 2n
-місних наборів: 2n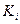 істинна, то на цьому наборі всі інші конституенти хибні.
істинна, то на цьому наборі всі інші конституенти хибні. 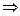
 на цьому наборі.
на цьому наборі.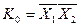
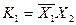
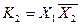
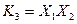

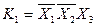

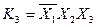
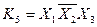
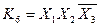
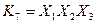
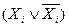 =1
=1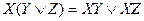 , у цьому разі дістають диз`юнкцію елементарних добутків з усіма попередніми буквами і ще однією
, у цьому разі дістають диз`юнкцію елементарних добутків з усіма попередніми буквами і ще однією 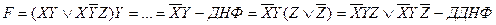
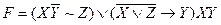 =...=
=...= 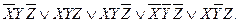

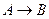 , яку ще ще називають імплікацією.
, яку ще ще називають імплікацією. дорівнює одиниці лише тоді, коли
дорівнює одиниці лише тоді, коли  , тобто на наборах де значення
, тобто на наборах де значення 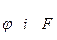 відповідно мають вигляд 0-0; 0-1; 1-1.
відповідно мають вигляд 0-0; 0-1; 1-1.
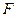
 на тих наборах на яких інша функція F=0, то
на тих наборах на яких інша функція F=0, то 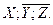 Власними частинами цього добутку будуть:
Власними частинами цього добутку будуть: 
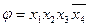 , а змінні
, а змінні  і
і 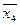 самостійно не входять як добутки. Тоді добуток
самостійно не входять як добутки. Тоді добуток 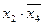 буде простою імплікантою функції F, бо
буде простою імплікантою функції F, бо  , а
, а 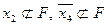 . Але добуток
. Але добуток  .
.