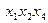Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні вимоги до алгоритмів.Содержание книги
Поиск на нашем сайте
1) Будь – який алгоритм застосовується до початкових даних і видає результати. У технічних термінах це означає, що алгоритм має входи і виходи. Крім того під час роботи алгоритму з’являються проміжні результати, що використовуються далі. Таким чином алгоритм має справу з початковими, проміжними та вихідними даними. Треба уточнити поняття даних, тобто які вимоги мають задовольняти об’єкти, щоб з ними могли працювати алгоритми. До алгоритмічних об’єктів відносяться: числа, вектори, матриці суміжності, формули,… Набір елементарних об’єктів утворюють скінченний алфавіт початкових символів (цифр, літер, тощо), з яких будуються інші об’єкти. 2) Дані для розміщення потребують пам’яті. Пам’ять вважається однорідною і дискретною, тобто складається з однакових комірок, причому кожна комірка може містити один символ алфавіту даних. Таким чином одиниці даних і пам’ять узгоджено. При цьому пам’ять може бути нескінченою. 3) Виконавцем алгоритму може виступати людина або технічний пристрій (ЕОМ).
Властивості алгоритмів. Навіть при виконанні всіх вимог до алгоритмів не всяка послідовність дій є алгоритмом. Для цього треба виконати кілька умов, що визначають властивості алгоритму: 1) Детермінованість: визначення кроків алгоритму: після кожного кроку зазначається, який крок слід робити далі або дається команда зупинки, після чого робота алгоритму вважається закінченою. Ця властивість означає, що застосування алгоритму до тих самих даних має привести до одного і того ж результату. 2) Масовість: алгоритм може бути використаний для розв’язання цілого класу задач одного типу з різними початковими даними (квадратні рівняння з різними коефіцієнтами). 3) Результативність: це значить, що після виконання певної кількості кроків робота алгоритму повинна зупинитись із вказівкою того, що вважати результатом. 4) Зрозумілість: алгоритм має бути зрозумілим конкретному виконавцю, який повинен виконати кожну команду у строгій відповідності з її призначенням. 5) Дискретність: можливість розбиття алгоритму на скінченну кількість етапів, причому результати попереднього етапу є вхідними для наступного. Отже, кожен алгоритм будується з розрахунку на конкретного виконавця і відповідним чином подається.
Потрібно розрізняти: - опис алгоритму (інструкцію чи програму); - механізм реалізації алгоритму (ЕОМ), який містить засоби запуску, зупинки, реалізації елементарних кроків, видачі результатів та забезпечення детермінованості, тобто керування ходом обчислення; - процес реалізації алгоритма, тобто послідовність кроків, яка буде породжена при застосуванні алгоритму до конкретних даних. Способи опису алгоритмів: словесний, табличний, графічний, псевдокод,… Алгоритм для ЕОМ найзручніше зображати графічно у вигляді схем. Схеми алгоритмів складаються з: - символів, що мають задане значення; - короткого пояснювального тексту; - сполучних ліній. Схема програми складається з: ü символів процесу, які показують фактичні операції оброблення даних (включаючи символи, що визначають шлях, якого варто дотримуватись з урахуванням логічних умов); ü лінійних символів, що показують потік керування; ü спеціальних символів, які використовують для полегшення написання та читання програми. Основні типи процесів оброблення інформації: o лінійний: оброблення інформації здійснюється послідовно, одна дія за іншою і кожний етап алгоритму виконується тільки один раз; o розгалужувальний: інформація обробляється по одному із двох можливих шляхів, тобто ті чи інші дії виконуються залежно від деякої умови; o циклічний: дії оброблення інформації потрібно виконати багаторазово.
Машина Тьюринга. Машина Тьюринга (МТ)– це математична модель пристрою, який породжує обчислювальні процеси. Її використовують для теоретичного уточнення поняття алгоритму та його дослідження. Названо цю модель ім’ям англійського математика А.Тьюринга, який запровадив її в 1936р. У кожній МТ є три частини: 1) стрічка поділена на комірки; 2) пристрій керування (ПК); 3) головка читання – запису (Г).
Із кожною МТ пов’язано два скінченних алфавіти: 1) алфавіт зовнішніх символів А; 2) алфавіт внутрішніх станів З різними МТ можна пов’язувати різні алфавіти. Алфавіт зовнішніх символів А часто називають зовнішнім, а його елементи – буквами. Один символ алфавіту А називають порожнім: L (
МТ працює у часі, який вважають дискретним, його моменти занумеровано: 1, 2,…У кожний момент часу стрічка містить скінченну кількість комірок. Головка пересувається вздовж стрічки, у кожний момент часу вона перебуває над певною коміркою стрічки, зчитує букву записану у цій комірці. У наступний момент головка залишається над цією ж коміркою (позначають Н) або пересувається на одну комірку вправо (П), або пересувається на одну комірку вліво (Л). Стрічка потенційно нескінченна в обидва боки, тобто до неї завжди можна додавати нові комірки як зліва так і справа. Алфавіт внутрішніх станів У кожний момент часу, залежно від букви, зчитаної із стрічки і внутрішнього стану машини, пристрій керування виконує такі дії: 1) змінює букву 2) пересуває головку в одному з напрямків Н, П, Л; 3) змінює внутрішній стан машини Таку дію пристрою керування називають командою і записують
D - напрямок пересування головки: Н, П, Л;
Вирази Робота МТ – це послідовність кроків одного за другим без пропусків, починаючи з першого. Роботу МТ повністю визначено, якщо в початковий момент задано: 1) слово на стрічці, тобто послідовність букв, записаних у комірках; 2) положення головки Г; 3) внутрішній стан машини. Сукупність цих трьох умов називається конфігурацією у даний момент часу. Зазвичай у початковий момент часу внутрішній стан машини -
Наприклад: початкова конфігурація така: Якщо в роботі МТ в момент часу Контрольні запитання.
1. Поняття алгоритму. 2. Етапи розв’язування задачі на ЕОМ. 3. Вимоги до алгоритмів. (*) 4. Властивості алгоритмів. (*) 5. Типи процесів оброблення інформації. (*) 6. Принцип роботи машини Тьюринга, його складові. (**)
Література: Ю.В. Нікольський, В.В.Пасічник, Ю.М. Щербина. Дискретна математика. Підручник для вищих навчальних закладів. Київ. 2007р. розділ 9.
Розділ 7. Контрольні завдання.
1. Множини А, В, С – підмножини множини дійсних чисел R. Знайти:
2. Накреслити діаграму Ейлера для трьох множин A, B, C, які утворюють множину F і позначте штриховкою її ділянку.
3. За допомогою таблиць істинності довести правильність рівносильності.
4. Провести логічні перетворення функції f. Одержати: 1) попередню форму; 2) ДНФ; 3) ДДНФ, область істинності; 4) КНФ; 5) ДКНФ, область хибності.
5. Для функцій задані номери наборів, на яких вона дорівнює одиниці. Мінімізувати цю функцію методом Квайна.
Зразки розв’язання.
1.Множини А, В, С – підмножини множини дійсних чисел R. Знайти: Розв’язання:
2. Накреслити діаграму Ейлера для трьох множин A, B, C, які утворюють множину F і позначте штриховкою її ділянку, якщо
3. За допомогою таблиць істинності довести правильність рівносильності.
4. Провести логічні перетворення функції 1) попередню форму; 2) ДНФ; 3) ДДНФ, область істинності; 4) КНФ; 5) ДКНФ, область хибності.
Розв’язання: 1) 2) 3) Область істинності: 110, 100, 001, 000, 111; 4)
5)
Область хибності: 010, 101, 011. 5. Для функцій задані номери наборів, на яких вона дорівнює одиниці. Мінімізувати цю функцію методом Квайна на наборах 7, 8, 10, 11, 13, 14, 15. Подамо функцію в ДДНФ:
Виконаємо всі можливі неповні склеювання першого члена, потім другого, третього і т. д. Проведемо всі можливі операції поглинання конституент одиниці і результат запишемо у таблицю (перше склеювання)
З таблиці видно, що всі конституенти одиниці поглинаються імплікантами, отриманими після склеювання. В результаті отримуємо таку функцію:
Проведемо друге склеювання конституент одиниці:
Будуємо імплікантну матрицю для одержаної функції F.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.83.84 (0.012 с.) |



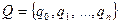
 ). Усі інші букви алфавіту А називають не порожніми. Комірку, у яку записано букву L називають порожньою.
). Усі інші букви алфавіту А називають не порожніми. Комірку, у яку записано букву L називають порожньою. - називають заключним внутрішнім станом,
- називають заключним внутрішнім станом,  - початковим внутрішнім станом. Пересування головки вздовж стрічки залежить від зчитаної букви та внутрішнього стану машини.
- початковим внутрішнім станом. Пересування головки вздовж стрічки залежить від зчитаної букви та внутрішнього стану машини. зчитану в момент часу
зчитану в момент часу  зі стрічки, на нову букву
зі стрічки, на нову букву  (або
(або  );
); в момент часу
в момент часу  , в якому машина перебуватиме в момент часу
, в якому машина перебуватиме в момент часу  (може бути
(може бути  ).
). , де
, де і
і 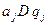 називають відповідно лівою і правою частинами цієї команди. У лівій частині не має жодної команди
називають відповідно лівою і правою частинами цієї команди. У лівій частині не має жодної команди  і А скінченні), їх сукупність називають програмою машини. Виконання однієї команди називають кроком.
і А скінченні), їх сукупність називають програмою машини. Виконання однієї команди називають кроком.


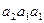 , початковий стан
, початковий стан  ,
,  ,
,  ,
,  ,
, 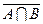 ,
, 

















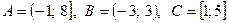





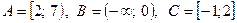




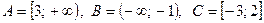





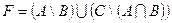

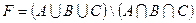




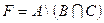

























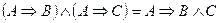





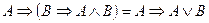
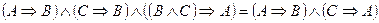
























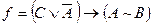




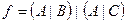



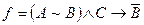








 .
.








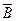
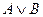
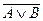


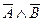
 - попередня форма;
- попередня форма;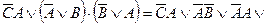
 -ДНФ;
-ДНФ;
 - ДДНФ;
- ДДНФ;
 - КНФ
- КНФ

 - ДКНФ;
- ДКНФ;










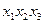


 - скорочена ДНФ
- скорочена ДНФ