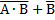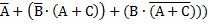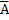Урок 1. Алгебра логики как средство представления информации в пк

УРОК 1. Алгебра логики как средство представления информации в ПК

Логика («logos») – мысль, слово, разум – наука, изучающая законы и формы мышления

Основоположник логики – древнегреческий ученый Аристотель (384 г. до н.э.). Логика по Аристотелю – это наука о выводе одних умозаключений из других сообразно их логической форме. Логику Аристотеля называют классической или формальной. Постепенно появилась математическая логика, основоположником которой считают Вильгельма Лейбница – немецкого философа и математика. Лейбниц предложил использовать в логике математическую символику и высказал мысль о применении в логике двоичной системы счисления. Большой вклад в развитие логики внес английский математик Джордж Буль. Он создал особую алгебру – алгебру логики или булеву алгебру. Булева алгебра используется для решения сложных математических задач в робототехнике, при разработке компьютеров и программ.

 

УРОК 2. Логические связки

Название	Эквивалентные обозначения	Таблица истинности
Унарные операции
Логическое отрицание (инверсия) – логическая операция, с помощью которой из одного высказывания порождается новое высказывание, которое будет называется отрицанием исходного (неверно, что…)	А не А not А Ā	А не А
Бинарные операции
Логическое сложение (дизъюнкция) – это логическая операция, образующая сложное высказывание из двух простых с помощью логического союза «ИЛИ». Строгая дизъюнкция – образует сложное высказывание истинное в том случае, если истинным является лишь один из его членов. Нестрогая дизъюнкция – образует сложное высказывание, истинное в том случае, когда истинно хотя бы одно из входящих в него суждений, а ложно, когда ложны оба входящие в него суждения	АvВ А или В А or В А+В	А В А или В
Логическое умножение (конъюнкция) – это логическая операция, образующая сложное высказывание из двух простых с помощью логического союза «И»	АΛВ А и В А and В А•В А&В	А В А и В
Импликация (следование) – логическая операция, образующая сложное высказывание из двух простых, посредством логической связки «если, то…»	А→В	А В А → В                         А→В=не А или В
Эквиваленция – это строгая импликация, объединяет суждения в сложные с помощью логического союза «если и только если, то…»	А-В А↔В АΞВ	А В А - В                         А-В=(неА и неВ)или(А и В) А-В=(А или неВ)и(неА или В)
Исключающее «ИЛИ»	А XOR В	А В А XOR В                         А XOR В= не (А-В)

Построение сложного выражения

В алгебре логики занимаются исследованием общих схем построения сложных высказываний. Высказывания обозначаются большими латинскими буквами.

 

Например:

«Если мы купим красные помидоры, то они будут спелые и вкусные»

А= «Мы купим красные помидоры»

В= «Помидоры будут спелые»

С= «Помидоры будут вкусные»

Тогда, структура высказывания будет: D = А → В • С

 

«Двери бывают с витражами или без них»

А= «Двери бывают с витражами»

В= «Двери бывают без витражей»

Тогда, структура высказывания будет: D = А + В

 

Упражнение

Составить структуру по следующим высказываниям:

1. Если не пойдет дождь, то не будет пасмурно и сыро.

2. Если мы соберем хворост или сухой травы, то разожжем костер и вскипятим чай.

 

УРОК 3-4. Построение таблиц истинности сложных выражений

Под логическим выражением понимают запись, которая может принимать логическое значение «истина» или «ложь». Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции.

В логике, как и в математике, существует приоритет выполнения операций:

Действия в скобках выполняются в первую очередь!

Если скобок нет, то тогда:

1. Отрицание

2. Логическое умножение

3. Логическое сложение

4. Импликация, эквиваленция

 

Упражнение

1. Построить таблицу истинности сложного выражения:

1. не(неА+В)+неС

2. не(А•В)•неС

3. не(А+неВ+С)

 

2. Какое логическое выражение равносильно выражению не(А+неВ)?

1. неА•В

2. не(А•В)

3. неА•неВ

4. неА+В

 

3. Какое логическое выражение равносильно выражению неА+А•неВ?

1. неА+В

2. неА•В

3. не(А•В)

4. не(А+В)

 

4. Какое логическое выражение равносильно выражению не(А+В)•неС?

1. неА+В+С

2. неА•неВ•С

3. не(А•В•С)

4. не(А+В+С)

УРОК 5-6. Законы логики

В алгебре логики выполняются основные законы, позволяющие производить тождественные преобразования логических выражений. Доказательства законов можно произвести на основании таблиц истинности для записей правой и левой стороны равенства соответственно. Законы алгебры логики служат для упрощения формул или приведения их к определенному виду. Под упрощением формулы, не содержащей операций импликации и эквивалентности, понимают равносильное преобразование, приводящее к формуле, которая содержит либо меньшее число операций (по сравнению с исходной), либо меньшее число переменных.

Закон	Описание	Для логического сложения	Для логического умножения
Переместительный (коммутативность)	Независимость от перестановки	А+В=В+А	А•В=В•А
Сочетательный (ассоциативность)	Независимость от порядка выполнения однотипных операций	А+(В+С)=(В+А)+С	А•(В•С)=(В•А)•С
Распределительный (дистрибутивность)	Правила раскрытия скобок и вынесение за скобки	А•(В+С)=(А•В)+(А•С)	А+(В•С)=(А+В)•(А+С)
Законы де Моргана	Отрицание вариантов, отрицание одновременной истинности
Идемпотенции	Отсутствие степеней и коэффициентов	А+А=А	А•А=А
Поглощения		А+(А•В)=А	А•(А+В)=А
Поглощения отрицания		А+(Ā•В)=А+В	А•(Ā+В)=А•В
Склеивания		(А•В)+(Ā•В)=В	(А+В)•(Ā+В)=В
Преобразования импликации		или А→В=А•В
Закон исключенного третьего и закон противоречия	Инверсия	А+Ā=1	А•Ā=0
Операции с константами	Действия с абсолютно- истинными и абсолютно- ложными высказываниями	А+0=А А+1=1	А•1=А А•0=0
Инволюция	Двойное отрицание	= А

Упражнение

1. Постройте логическую формулу по высказыванию: «Неверно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет ветра»

2. Упростить выражение:

a) А•не(неВ+С)

b) не((А+В)→не(В+С))

3. Каково наибольшее целое число Х, при котором истинно высказывание:

(35<X•X)→(X<(X-3))

4. Какое из приведённых имен удовлетворяет логическому условию:
(первая буква согласная → вторая буква согласная)•(предпоследняя буква гласная → последняя буква гласная)?

1) КРИСТИНА 2) МАКСИМ 3) СТЕПАН 4) МАРИЯ

5. Для какого из указанных значений X истинно высказывание: не((X > 2)→(X > 3))?

X	Y	Z	F

1) 1 2) 2 3) 3 4) 4

6. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:

Какое выражение соответствует F?

1) неX•неY•неZ 2) X•Y•Z 3) X+Y+Z 4) неX+неY+неZ

7. Дано логическое выражение, зависящее от 5 логических переменных:

X1•неX2•X3•неX4•X5

Сколько существует различных наборов значений переменных, при которых выражение ложно?

1) 1 2) 2 3) 31 4) 32

УРОК 7-8. Преобразование логических выражений с помощью законов логики

Упростите логические выражения, используя законы логики:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

Упражнение

1. Построим схему следующего высказывания:

Схему строим как конструктор, справа налево в порядке действий:

1.

2.

3.

4.

Шаг 1. Рисуем три входных высказывания	Шаг 2. Строим блок «НЕ»
Шаг 3. Строим блок «НЕ»	Шаг 4. Строим блок «И»
Шаг 5. Строим блок «ИЛИ»

2. Построить схему следующего высказывания:

Схему строим как конструктор, справа налево в порядке действий:

1. Рисуем три входных высказывания: А, В, С

2. Строим блок «НЕ»:

3. Строим блок «НЕ»:

4. Строим блок «НЕ»:

5. Строим блок «И»:

6. Строим блок «И-НЕ»:

7. Строим блок «И»:

8. Строим блок «ИЛИ»:

УРОК 1. Алгебра логики как средство представления информации в ПК

Логика («logos») – мысль, слово, разум – наука, изучающая законы и формы мышления

Основоположник логики – древнегреческий ученый Аристотель (384 г. до н.э.). Логика по Аристотелю – это наука о выводе одних умозаключений из других сообразно их логической форме. Логику Аристотеля называют классической или формальной. Постепенно появилась математическая логика, основоположником которой считают Вильгельма Лейбница – немецкого философа и математика. Лейбниц предложил использовать в логике математическую символику и высказал мысль о применении в логике двоичной системы счисления. Большой вклад в развитие логики внес английский математик Джордж Буль. Он создал особую алгебру – алгебру логики или булеву алгебру. Булева алгебра используется для решения сложных математических задач в робототехнике, при разработке компьютеров и программ.