
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм мінімізації дкнф за квайномСодержание книги
Поиск на нашем сайте
1.У ДКНФ для F = F( 2. Виконати всі операції неповного склеювання й поглинання імпліцент з (n -1) змінними, отриманих на першому кроці склеювання, потім - імпліцент з (n-2) змінними й т.ін., поки ця процедура можлива. Урезультаті буде отримана скорочена КНФ. 3.3 допомогою скороченої КНФ побудувати імпліцентну матрицю. 4. В імпліцентній матриці відшукати набори простих імпліцент, які накривають усі конституенти нуля логічної функції, що подана в ДКНФ і мінімізується. 5. Серед цих наборів знайти такі, які в сумі містять мінімальну кількість літер. 6. Одержати мінімальні КНФ, об'єднавши прості імпліценти набора з їх мінімальною кількістю знаками кон'юнкції. Серед них вибрати одну найбільш ефективну для реалізації. Приклад. Знайти мінімальну КНФ логічної функції, що дорівнює нулю на наборах з номерами 0, 1, 2, 3, 7, 9, 12, 13, 15 і одиниці - на решті. 1. Знайдемо скорочену КНФ: 2. Виконаємо всі можливі операції неповного склеювання й поглинання:
Урезультаті отримуємо В одержаному виразі знову виконаємо всі операції неповного склеювання й поглинання У кінцевому підсумку отримуємо До останнього виразу операції неповного склеювання й поглинання застосувати не можна, і тому він є скороченою КНФ. 3. Побудуємо імпліценгну матрицю. До мінімальної форми слід включити імпліценти Унаслідок вибору цих імпліцент опиняються перекритими стовпці з номерами 1, 2, 3, 4, 7, 8. Решту рядків 5, 6, і 9 можна перекрити двома способами: імпліцентами Таким чином, задана функція має дві мінімальні форми з однаковим кількістю літер: Слід зазначити, що кількість літер у мінімальних КНФ і ДНФ логічної функції різна. Тому при розв'язуванні задач мінімізації логічних функцій потрібно знайти як диз'юнктивні, так і кон'юнктивні мінімальні нормальні форми і вибрати серед них форму з найменшою кількістю літер. 35. Імпліцентна матриця для одержання мінімальної КНФ. Тупікові і мінімальні КНФ. Приклади. Теорема Квайна для КНФ. Якщо в ДКНФ логічної функції F про- Вести всі операції неповного склеювання, а потім всі операції поглинан- Ня, то вийде скорочена КНФ цієї функції, тобто кон'юнкція всіх її прос- Тих імпліцент. За теоремою Квайна для мінімізації логічної функції F, поданої в КНФ, її спочатку треба перетворити в ДКНФ, а потім виконати такі кроки: 1. В ДКНФ F = F(х1, х2,..., хn) здійснити всі операції неповного скле- ювання, а потім поглинання конституент нуля. 2. Здійснити всі операції неповного склеювання і поглинання імплі- цент з (n - 1)- ю змінними, отриманих на першому кроці склеювання, потім - імпліцент з (n- 2)- а змінними і т.д., доки процедура можлива. 3. По одержаній скороченій КНФ побудувати імпліцентну матрицю. 4. В імпліцентній матриці відшукати набори простих імпліцент, які накривають усі конституенти нуля логічної функції, яка подана в ДКНФ і мінімізується. 5. Серед цих наборів знайти такі, які в сумі містять мінімальне число літер. 6. Одержати мінімальні КНФ, об'єднавши прості імпліценти знаками кон'юнкції. Серед них вибрати одну найбільш ефективну для реалізації. Приклад. Знайти мінімальну КНФ логічної функції, що дорівнює ну- лю на наборах з номерами 0, 1, 2, 3, 7, 9, 12, 13, 15 і одиниці - на решті. 1.Знайдемо ДКНФ: 2.Виконаємо всі можливі операції неповного склеювання і поглинан- ня: У результаті дістанемо: В одержаному виразі знову виконаємо всі операції неповного склею- вання і поглинання У кінцевому підсумку дістанемо: До останнього виразу операції неповного склеювання і поглинання за- стосувати не можна, і тому він є скороченою КНФ. 3. Побудуємо імпліцентну матрицю (див. табл. 1). До мінімальної форми слід включити імпліценти Внаслідок вибору цих імпліцент опиняються перекритими стовпці з номерами 1, 2, 3, 4, 7, 8. Стовпці 5, 6, і 9 можна перекрити двома способами: Таким чином, задана функція має дві мінімальні форми з однаковим числом літер: 1. 2. Слід зазначити, що кількості літер в мінімальних КНФ і ДНФ логічної функції різні. Тому при розв'язуванні задач мінімізації логічних функцій потрібно знайти як диз'юнктивні, так і кон'юнктивні мінімальні нормальні форми і вибрати серед них форму з найменшою кількістю літер. Мінімальна КНФ - це КНФ, що містить мінімальну кількість букв в порівнянні з будь-якої іншої, еквівалентної КНФ. Тупікова КНФ - це кон'юнкція простих елементарних диз'юнкцій, жодну з яких виключити не можна. 36. Метод карт Карно-Вейча для мінімізації булевих функцій, представлених в ДДНФ. Приклади. Ціллю мінімізації є знаходження мінімальної з тупикових ДНФ (КНФ), тобто знаходження мінімального покриття даної функції. Для цього необхідно побудувати всі можливі тупикові ДНФ (КНФ), використовуючи операції склеювання та поглинання для даної функції. Методика Карно і Вейча дозволяє виконати зазначені операції графічно. Карта Карно для ДНФ (діаграма Вейча — для КНФ) є аналогом таблиці істинності, зображеній у спеціальній формі. Значення змінних розташовані у заголовках рядків і стовпців карти. Кожній конституенті одиниці функції відповідає одна клітка (комірка) таблиці. Нуль абоодиниця в клітці визначає значення функції на даній інтерпретації. Значення змінних розташовані так, щоб сусідні (що мають спільну межу) рядки і стовпці таблиці відрізнялись значенням тільки однієї змінної. Тому запис інтерпретацій двох змінних у порядку (0, 0), (0, 1), (1, 0), (1, 1) неприпустимий, оскільки сусідні набори (0, 1) і (1, 0) відрізняються значеннями обох змінних. У картах Карно інтерпретації двох змінних розташовуються у такій послідовності: (0, 0), (0, 1), (1, 1), (1,0). У цій послідовності перша та остання інтерпретації також відрізняються значенням тільки однієї змінної, тому перший і останній рядки (стовпці) таблиці вважаються сусідніми (протилежні границі таблиці вважаються співпадаючими). При такому розташуванні мінтер-ми, до яких застосовна операція склеювання, розташовуються у сусідніх клітках карти, і склеювання проводиться графічноза допомогою об єднання кліток у групи. Карти Карно для функцій двох змінних мають вид таблиці 2х2, де стовпці відповідають значенням першої змінної, а рядки — значенням другої змінної. На рис. 4.1 зображено структури картиКарно, в клітках вказано відповідні мінтерми увиді формул з абстрактними змінними.
Структура карти Карно для функцій трьох змінних має вид таблиці 2 х 4, дестовпці відповідають всіляким наборам значень перших двох змінних, а рядки — значенням Oilтретьої змінної (рис. 4.2). В клітках структури вказано відповідні мінтерми з абстрактними змінними.
Розв'язок. Побудова карти Карно для заданої функції: поміщаємо одиниці до кліток, що відповідають мінтермам, які присутні в даній ДДНФ, і нулі — в решту кліток (рис. 4.3).
До конституентів одиниці, що відповідають будь-яким двом сусіднім кліткам, можна застосувати операцію склеювання, оскільки вони відрізняються тільки однією змінною. Зауважимо, що на карті Карно для функції трьох змінних кожна клітка має три сусідні клітки, на карті Карно для функції чотирьох змінних — чотири, на карті Карно для функції п'яти змінних — п'ять тощт. При цьому для кліток на карті Карно функції трьох змінних, розташованих у крайньому правому або у крайньому лівому стовпцях, сусідніми є клітки, що розташовані безпосередньо зліва (або справа), вище (або нижче) у сусідньому рядку, і крайня ліва (або права) у тому ж рядку. Як приклад на рис. 4.4 відзначено клітки, сусідні з клітками А і В.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 613; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |

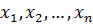 ) виконати всі операції неповного склеювання, а потім поглинання конституент нуля.
) виконати всі операції неповного склеювання, а потім поглинання конституент нуля.

 Для конкретної булевої функції карта Карно заповнюється таким чином. У клітках, що відповідні інтерпретаціям, на яких функція дорівнює одиниці, записують одиниці. Ці клітки відповідають конституентам одиниці, що присутні у ДДНФ функції. В інші клітки записують нулі.
Для конкретної булевої функції карта Карно заповнюється таким чином. У клітках, що відповідні інтерпретаціям, на яких функція дорівнює одиниці, записують одиниці. Ці клітки відповідають конституентам одиниці, що присутні у ДДНФ функції. В інші клітки записують нулі.




