
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Досконала диз'юнктивна нормальна форма (дднф). Теорема про існування дднф логічної функції. Доведення. Алгоритм одержання конституенти одиниці та дднф. ПрикладСодержание книги
Поиск на нашем сайте Доскона́лою диз'юнкти́вною норма́льною фо́рмою (ДДНФ) булевої функції називається диз'юнкція тих конституент одиниці, які перетворюються в одиницю на тих самих наборах змінних, що й задана функція. ДДНФ повинна задовольняти наступним умовам: · в ній немає однакових доданків; · жоден із доданків не містить двох однакових співмножників; · жоден із доданків не містить змінну разом із її запереченням; · в кожному окремому доданку є як співмножник або змінна xi, або її заперечення для будь-якого i = 1, 2, …, n. Для будь-якої функції булевої алгебри існує своя ДДНФ, причому тільки одна. Для того, щоб отримати ДДНФ функції, потрібно скласти її таблицю істинності. Наприклад, візьмемо одну з таблиць істинності з статті Метод Куайна, в якій знаходження ДДНФ зустрічається декілька разів:
В комірках результату · · · · Нульові значення — тут всі змінні представлені нулями — записуються в кінцевому виразі інверсією цієї змінної. Перший член ДДНФ даної функції має такий вигляд: · · · ·
Таким чином аналізуються всі комірки Досконала ДНФ цієї функції:
Поняття імпліканти і простої імпліканти. Основні теореми - властивості імпліканти. Доведення. Приклади.
Поняття скороченої ДНФ. Операції, які застосовуються при отриманні скороченої ДНФ, їх логічний запис та доведення. Приклад. Операції повного і неповного склеювання в ДНФ, операція поглинання і розгорнення. Приклади. Доведення. Теорема Квайна для ДДНФ. Доведення. Особливості застосування. Алгоритм мінімізації ДДНФ за Квайном. Приклад. 27. Імплікантні матриці для одержання мінімальної ДНФ. Тупікові і мінімальні ДНФ. Приклад.
28. Поняття про кон'юнктивну нормальну форму (КНФ). Елементарна сума. Конституента нуля. Основні теореми для констигуенти нуля і її наслідки.
29. Досконала кон'юнктивна нормальна форма (ДКНФ). Теорема про існування ДКНФ логічної функції. Доведення. Алгоритм одержання конституенти нуля і ДКНФ. Приклади.
30. Поняття імпліценти і простої імпліценти. Основні теореми - властивості імпліценти. Доведення. Приклади.
31. Поняття скороченої КНФ. Операції, які застосовуються при отриманні скороченої КНФ, їх логічний запис та доведення. Приклад.
32. Операції повного і неповного склеювання в КНФ. Операції поглинання і розгорнення. Приклади. Доведення.
33. Теорема Квайна для ДКНФ. Доведення. Особливості застосування. Теорема Квайнадля ДКНФ. Якщо в ДКНФ логічної функції F виконати всі операції неповного склеювання, а потім усі операції поглинання, то отримаємо скорочену КНФ цієї функції, тобто конюнкцію всіх її простих імпліцент. Доведення. Припустимо, що після виконання всіх операцій неповного склеювання, а потім поглинання отримана ДНФ буде містити у вигляді кон'юнкції член q, який не є простою імплікантою. Тоді до цієї функції, крім члена q, самостійно входить також у вигляді кон'юнкції якась його частина р, яка є простою імплікантою. Це означає,що функція F буде містити імпліканту q і просту імпліканту р увигляді їх диз'юнкції р\/q. Але q = Особливості Для мінімізації логічної функції Р, поданої в КНФ, з допомогою теореми Квайна її спочатку треба перетворити на ДКНФ.
34. Алгоритм мінімізації ДКНФ за Квайном. Приклад.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1591; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

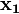
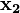
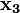
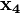
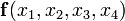
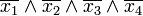
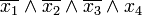
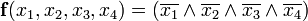

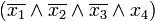
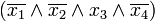
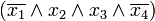
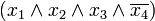
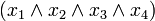



































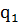 р. Тоді член q згідно з рівністю р\/q= р\/
р. Тоді член q згідно з рівністю р\/q= р\/ 


