Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило склеювання кліток і запису мінімальної ДНФСодержание книги
Поиск на нашем сайте
1. Будується карта Карно, що відповідає даній функції.
2. Клітки об'єднуються у групи, що позначають операції склеювання. В об'єднанні беруть участь тільки сусідні клітки, в яких знаходяться одиниці.
3. В групу можні об'єднати тільки кількість кліток, що дорівнює 2 n , n— 1, 2, 3,.... При цьому група може мати тільки прямокутну або квадратну форму. Задача склеювання полягає у знаходженні набору максимальних груп кліток. Максимальна група — це група, яка не входить цілком у жодну іншу групу і відповідає простій імпліканті функції. Кількість груп у такому наборі повинна бути мінімальною, оскільки така група відповідає мінімальній тупиковій ДНФ. Кожна одиниця карти Карно повинна входити хоча б до однієї групи, що забезпечує покриття функції одержаним набором імплікант. 5.Кожна група кліток, що одержана після склеювання, відповідає тій імпліканті функції, реальні змінні якої мають однакове значення для всіх кліток групи. Змінні беруться без заперечення, якщо їм відповідають одиничні значення, і із запереченням — в іншому випадку.
6.Диз'юнкція всіх одержаних простих імплікант зображує результат мінімізації формули і є мінімально ДНФ.
Приклад. Знайти мінімальну ДНФ функції з попереднього прикладу. Розв'язок. Опускаючи нулі на рис. 4.3, записуємо вихідну карту Карно у такому вигляді (рис. 4.5). Графічно склеювання позначається об'єднанням сусідніх одиниць таблиці у групи, результатом чого є дві імпліканти А і В (рис. 4.6).
не тільки крайній правий та крайній лівий стовпці, але також крайній верхній і крайній нижній рядки. 37. Метод карт Карно-Вейча для мінімізації булевих функцій, представлених в ДКНФ. Приклади.
Мінімізація на множині КНФ Для мінімізації булевої функції на множині КНФ використовуються діаграми Вейча. їх побудова аналогічна картам Карно. На карті позначаються клітки, що відповідають інтерпретаціям, на яких функція дорівнює нулю. Після цього проводиться склеювання кліток, що містять нулі і формування мінімальної КНФ. Склеювання кліток здійснюється за тими ж правилами, що й при диз'юнктивній мінімізації. Кожна група кліток, що одержана в результаті склеювання, відповідає диз'юнкції тільки тих змінних, які мають однакове значення для всіх кліток групи. Змінні беруться без заперечення, якщо їм відповідає нульове значення, і із запереченням — в іншому випадку. Кон'юнкція одержаних елементарних диз'юнкцій є результатом мінімізації формули.
Розв'язок. Дана функція обертається на нуль на таких наборах:(0,0,0,0,0),(0,0,0,0,1),(0,0,1,0,0),(0,0,1,1,0), (0, 1, 1, 0, 0), (0, 1, 1, 1, 0), (1, 0, 0, 0, 0), (1, 0, 0, 0, 1), (1, 1, 1,0,0), (1, 0, 1, 1, 1). Побудуємо карту Карно для цієї функції (рис. 4.11).
Запишемо мінімальну КНФ, поєднавши знаками кон'юнкції елементарні диз'юнкції:
38. Мінімізація неповністю означених булевих функцій. Приклад. Якщо для розв'язку задачі використовуються не всі набори вхідних даних, то припустиме будь-яке значення функції на невикористовуваних інтерпретаціях і така функція називається частково визначеною. Іншими словами, функція не визначена на вказаних інтерпретаціях. При мінімізації такі функції до-визначаються так, щоб одержати найбільш економічну мінімальну ДНФ (КНФ). Приклад. Функція f(x, у, z, t) дорівнює одиниці на наборах (0, 0, 1, 0), (0, 1, 1, 0), (1, 0, 1, 0), (1, 0, 0, 0) і не визначена, якщо ху = 1. Необхідно побудувати мінімальну ДНФ.
Мінімальна ДНФ /(х, у, z, t) = A v В - zt v xt.
Метод карт Карно не є формальним і складний у реалізації. Крім того, він не зручний у застосуванні до функцій з кількістю змінних більше шести. Інший метод мінімізації, який буде розглянутий нижче, придатний для програмної реалізації і може застосовуватися при великій кількості змінних.
39. Перетворення ДНФ у КНФ. Будь-яку ДНФ можна привести до КНФ 3-ма способами: 1) Нехай деяка функція Р має вигляд ДНФ виконує наступне застосування закону подвійного заперечення:далі нижня риска згідно правила Де Моргана опускається на окремі висловлювання. Вираз під рискою приводить до вигляду ДНФ,після чого знову опускається риска на окремі висловлювання. Результат і буде КНФ 2) ДНФ перетворити до вигляду КНФ за дистрибутивною ознакою А \/ ВС=(А\/В) (А\/С) 3) Нехай деяка формула Р має вигляд ДНФ знаходимо для неї двоїсту формулу р* та приводить до ДНФ позначають її як а* після цього знаходимо формулу,що є двоїстою до (а*)*=а вона і буде КНФ при чому згідно принципу двоїстості А=Р
Приклад. Привести до КНФ функцію,задану в ДНФ:
f(x,y,z) = x
Використовуємо закон де Моргана, розкривши потім дужки і видаляючи зайві коньюнкції, отримаємо:
Використаємо до цього виразу закон Де Моргана отримаємо:
f(x,y,z) =
Це і є КНФ яку ми шукали для заданої функції.
40. Одержання мінімальних КНФ за допомогою диз'юнктивних форм. Приклад. Логічні функції, подані у ДНФ, після мінімізації можна перетворити в КНФ, використовуючи доведені нижче властивості логічних функцій. Припустимо, що дана логічна функція F = F(х1, х2,..., хn), яка приймає на наборах j1, j2, …, jm значення одиниці, а на наборах i1, i2, …, ip, де p=2n-m - значення нуля. Тоді має місце така теорема. Теорема 1. Диз'юнкція всіх конституент одиниці Ki1 \/ Ki2 \/ … \/ Kip, що не входять до ДДНФ логічної функції F, є запереченням цієї функції: Ki1 \/ Ki2 \/ … \/ Kip= Теорема 2. КНФ логічної функції Р, одержана з мінімальної ДНФ функції Р після її перетворення за допомогою формул де Моргана, також Буде мінімальною.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.138 (0.008 с.) |

 Оскільки при мінімізації на множині ДНФ у склеюванні беруть участь тільки клітки, що містять одиниці, нулі в картах Карно, як правило, не вказують і мають на увазі, що порожні клітки містять нулі.
Оскільки при мінімізації на множині ДНФ у склеюванні беруть участь тільки клітки, що містять одиниці, нулі в картах Карно, як правило, не вказують і мають на увазі, що порожні клітки містять нулі.


 Розглянемо застосування карт Карно для мінімізації функцій, що залежать від чотирьох змінних. Карта Карно для функції чотирьох змінних має розмір 4x4. Кожна клітка має чотири сусідніх. Правила склеювання кліток і запису результуючої формули залишаються попередніми. Відмінність полягає в тому, що сусідніми необхідно вважати
Розглянемо застосування карт Карно для мінімізації функцій, що залежать від чотирьох змінних. Карта Карно для функції чотирьох змінних має розмір 4x4. Кожна клітка має чотири сусідніх. Правила склеювання кліток і запису результуючої формули залишаються попередніми. Відмінність полягає в тому, що сусідніми необхідно вважати

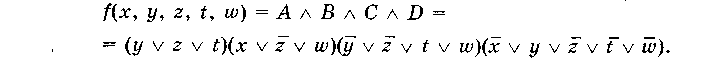
 Розв'язок. Складемо карту Карно для заданої функції (рис. 4.12).
Розв'язок. Складемо карту Карно для заданої функції (рис. 4.12). \/
\/  у\/х
у\/х