Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Біноміальна система числення з двійковим алфавітом. Діапазон, обмеження, характеристики та властивості.Содержание книги
Поиск на нашем сайте Біноміальна система числення з двійковим алфавітом. Діапазон, обмеження, характеристики та властивості.
2. Кодотвірна функція біноміальної системи числення з двійковим алфавітом. Нумерація біноміальних чисел.
Алгоритм генерування двійкових біноміальних комбінацій.
Перетворення чисел степеневої системи числення в біноміальну систему числення з двійковим алфавітом. Поняття про алгебру логіки і обчислення висловлень. Алгебра логіки (Булева логіка, двійкова логіка, двійкова алгебра) — розділ математичної логіки, що вивчає систему логічних операцій над висловлюваннями. Тобто, представлення логіки у вигляді алгебраїчної структури.
Базовими елементами, якими оперує алгебра логіки, є висловлювання. Висловлювання будуються над множиною {B,
а також константи - логічний нуль 0 і логічна одиниця 1. Логічні операції Простим і найширше вживаним прикладом такої алгебраїчної системи є множина B, що складається всього з двох елементів: B = { Хибність(0), Істина(1) } Як правило, в математичних виразах Хибність ототожнюється з логічним нулем, а Істина - з логічною одиницею, а операції заперечення(НІ), кон'юнкції(ТА) і диз'юнкції(АБО) визначаються в звичному нам розумінні. Легко показати, що на цій множині B можна задати чотири унарні і шістнадцять бінарних відношень і усі вони можуть бути отримані через суперпозицію трьох обраних операцій. Спираючись на цей математичний інструментарій, логіка висловлювань вивчає висловлювання і предикати. Також вводяться додаткові операції, такі як еквівалентність Логіка висловлювань послужила основним математичним інструментом при створенні комп'ютерів. Вона легко перетворюється в бітову логіку: істинність висловлювання позначається одним бітом (0 - ХИБНІСТЬ, 1 - ІСТИНА); тоді операція Згодом булева алгебра була узагальнена від логіки висловлювань шляхом введення характерних для логіки висловлювань аксіом. Це дозволило розглядати, наприклад, логіку кубітів, потрійну логіку(коли є три варіанти істинності висловлювання: "істина", "хибність" і "невизначено") та ін.
Істинне і хибне висловлення. Просте і складне висловлення. Приклади.
7. Основні логічні операції: константа нуля, константа одиниці, операції "НЕ", "І", "АБО". 8. Логічні операції: "імплікація", "заборона", "рівнозначність", "нерівнозначність". Приклади. 9. Логічні операції "Шеффера", "Пірса", "Змінна". Приклади.
Поняття про логічний закон, логічне протиріччя і твердження, яке логічно виконується. Приклади.
Основні закони алгебри логіки. Приклади.
Поняття набору логічної функції. Таблиця істинності. Теорема про число наборів від п аргументів функції. Доведення.
13. Поняття про логічну функцію та її аргументи. Інверсна функція. Теорема про кількість функцій від 2" аргументів. Доведення.
Логічні функції двох аргументів. Визначити їх кількість і дати назву. Привести таблиці істинності. Доведення логічних тверджень і законів за допомогою таблиць істинності. Приклади. Привести доведення за допомогою таблиць істинності правила де Моргана, імплікації, рівнозначності.
Привести і довести співвідношення між двома аргументами, один із яких приймає значення 1 або 0. 18. Привести і довести співвідношення між двома аргументами , коли
Поняття імпліканти і простої імпліканти. Основні теореми - властивості імпліканти. Доведення. Приклади.
Поняття скороченої ДНФ. Операції, які застосовуються при отриманні скороченої ДНФ, їх логічний запис та доведення. Приклад. Особливості Для мінімізації логічної функції Р, поданої в КНФ, з допомогою теореми Квайна її спочатку треба перетворити на ДКНФ.
34. Алгоритм мінімізації ДКНФ за Квайном. Приклад. Тих імпліцент. За теоремою Квайна для мінімізації логічної функції F, поданої в КНФ, її спочатку треба перетворити в ДКНФ, а потім виконати такі кроки: 1. В ДКНФ F = F(х1, х2,..., хn) здійснити всі операції неповного скле- ювання, а потім поглинання конституент нуля. 2. Здійснити всі операції неповного склеювання і поглинання імплі- цент з (n - 1)- ю змінними, отриманих на першому кроці склеювання, потім - імпліцент з (n- 2)- а змінними і т.д., доки процедура можлива. 3. По одержаній скороченій КНФ побудувати імпліцентну матрицю. 4. В імпліцентній матриці відшукати набори простих імпліцент, які накривають усі конституенти нуля логічної функції, яка подана в ДКНФ і мінімізується. 5. Серед цих наборів знайти такі, які в сумі містять мінімальне число літер. 6. Одержати мінімальні КНФ, об'єднавши прості імпліценти знаками кон'юнкції. Серед них вибрати одну найбільш ефективну для реалізації. Приклад. Знайти мінімальну КНФ логічної функції, що дорівнює ну- лю на наборах з номерами 0, 1, 2, 3, 7, 9, 12, 13, 15 і одиниці - на решті. 1.Знайдемо ДКНФ: 2.Виконаємо всі можливі операції неповного склеювання і поглинан- ня: У результаті дістанемо: В одержаному виразі знову виконаємо всі операції неповного склею- вання і поглинання У кінцевому підсумку дістанемо: До останнього виразу операції неповного склеювання і поглинання за- стосувати не можна, і тому він є скороченою КНФ. 3. Побудуємо імпліцентну матрицю (див. табл. 1). До мінімальної форми слід включити імпліценти Внаслідок вибору цих імпліцент опиняються перекритими стовпці з номерами 1, 2, 3, 4, 7, 8. Стовпці 5, 6, і 9 можна перекрити двома способами: Таким чином, задана функція має дві мінімальні форми з однаковим числом літер: 1. 2. Слід зазначити, що кількості літер в мінімальних КНФ і ДНФ логічної функції різні. Тому при розв'язуванні задач мінімізації логічних функцій потрібно знайти як диз'юнктивні, так і кон'юнктивні мінімальні нормальні форми і вибрати серед них форму з найменшою кількістю літер. Мінімальна КНФ - це КНФ, що містить мінімальну кількість букв в порівнянні з будь-якої іншої, еквівалентної КНФ. Тупікова КНФ - це кон'юнкція простих елементарних диз'юнкцій, жодну з яких виключити не можна. 36. Метод карт Карно-Вейча для мінімізації булевих функцій, представлених в ДДНФ. Приклади. Ціллю мінімізації є знаходження мінімальної з тупикових ДНФ (КНФ), тобто знаходження мінімального покриття даної функції. Для цього необхідно побудувати всі можливі тупикові ДНФ (КНФ), використовуючи операції склеювання та поглинання для даної функції. Методика Карно і Вейча дозволяє виконати зазначені операції графічно. Карта Карно для ДНФ (діаграма Вейча — для КНФ) є аналогом таблиці істинності, зображеній у спеціальній формі. Значення змінних розташовані у заголовках рядків і стовпців карти. Кожній конституенті одиниці функції відповідає одна клітка (комірка) таблиці. Нуль абоодиниця в клітці визначає значення функції на даній інтерпретації. Значення змінних розташовані так, щоб сусідні (що мають спільну межу) рядки і стовпці таблиці відрізнялись значенням тільки однієї змінної. Тому запис інтерпретацій двох змінних у порядку (0, 0), (0, 1), (1, 0), (1, 1) неприпустимий, оскільки сусідні набори (0, 1) і (1, 0) відрізняються значеннями обох змінних. У картах Карно інтерпретації двох змінних розташовуються у такій послідовності: (0, 0), (0, 1), (1, 1), (1,0). У цій послідовності перша та остання інтерпретації також відрізняються значенням тільки однієї змінної, тому перший і останній рядки (стовпці) таблиці вважаються сусідніми (протилежні границі таблиці вважаються співпадаючими). При такому розташуванні мінтер-ми, до яких застосовна операція склеювання, розташовуються у сусідніх клітках карти, і склеювання проводиться графічноза допомогою об єднання кліток у групи. Карти Карно для функцій двох змінних мають вид таблиці 2х2, де стовпці відповідають значенням першої змінної, а рядки — значенням другої змінної. На рис. 4.1 зображено структури картиКарно, в клітках вказано відповідні мінтерми увиді формул з абстрактними змінними.
Структура карти Карно для функцій трьох змінних має вид таблиці 2 х 4, дестовпці відповідають всіляким наборам значень перших двох змінних, а рядки — значенням Oilтретьої змінної (рис. 4.2). В клітках структури вказано відповідні мінтерми з абстрактними змінними.
Розв'язок. Побудова карти Карно для заданої функції: поміщаємо одиниці до кліток, що відповідають мінтермам, які присутні в даній ДДНФ, і нулі — в решту кліток (рис. 4.3).
До конституентів одиниці, що відповідають будь-яким двом сусіднім кліткам, можна застосувати операцію склеювання, оскільки вони відрізняються тільки однією змінною. Зауважимо, що на карті Карно для функції трьох змінних кожна клітка має три сусідні клітки, на карті Карно для функції чотирьох змінних — чотири, на карті Карно для функції п'яти змінних — п'ять тощт. При цьому для кліток на карті Карно функції трьох змінних, розташованих у крайньому правому або у крайньому лівому стовпцях, сусідніми є клітки, що розташовані безпосередньо зліва (або справа), вище (або нижче) у сусідньому рядку, і крайня ліва (або права) у тому ж рядку. Як приклад на рис. 4.4 відзначено клітки, сусідні з клітками А і В.
Мінімізація на множині КНФ Для мінімізації булевої функції на множині КНФ використовуються діаграми Вейча. їх побудова аналогічна картам Карно. На карті позначаються клітки, що відповідають інтерпретаціям, на яких функція дорівнює нулю. Після цього проводиться склеювання кліток, що містять нулі і формування мінімальної КНФ. Склеювання кліток здійснюється за тими ж правилами, що й при диз'юнктивній мінімізації. Кожна група кліток, що одержана в результаті склеювання, відповідає диз'юнкції тільки тих змінних, які мають однакове значення для всіх кліток групи. Змінні беруться без заперечення, якщо їм відповідає нульове значення, і із запереченням — в іншому випадку. Кон'юнкція одержаних елементарних диз'юнкцій є результатом мінімізації формули.
Розв'язок. Дана функція обертається на нуль на таких наборах:(0,0,0,0,0),(0,0,0,0,1),(0,0,1,0,0),(0,0,1,1,0), (0, 1, 1, 0, 0), (0, 1, 1, 1, 0), (1, 0, 0, 0, 0), (1, 0, 0, 0, 1), (1, 1, 1,0,0), (1, 0, 1, 1, 1). Побудуємо карту Карно для цієї функції (рис. 4.11).
Запишемо мінімальну КНФ, поєднавши знаками кон'юнкції елементарні диз'юнкції:
38. Мінімізація неповністю означених булевих функцій. Приклад. Якщо для розв'язку задачі використовуються не всі набори вхідних даних, то припустиме будь-яке значення функції на невикористовуваних інтерпретаціях і така функція називається частково визначеною. Іншими словами, функція не визначена на вказаних інтерпретаціях. При мінімізації такі функції до-визначаються так, щоб одержати найбільш економічну мінімальну ДНФ (КНФ). Приклад. Функція f(x, у, z, t) дорівнює одиниці на наборах (0, 0, 1, 0), (0, 1, 1, 0), (1, 0, 1, 0), (1, 0, 0, 0) і не визначена, якщо ху = 1. Необхідно побудувати мінімальну ДНФ.
Мінімальна ДНФ /(х, у, z, t) = A v В - zt v xt.
Метод карт Карно не є формальним і складний у реалізації. Крім того, він не зручний у застосуванні до функцій з кількістю змінних більше шести. Інший метод мінімізації, який буде розглянутий нижче, придатний для програмної реалізації і може застосовуватися при великій кількості змінних.
39. Перетворення ДНФ у КНФ. Будь-яку ДНФ можна привести до КНФ 3-ма способами: 1) Нехай деяка функція Р має вигляд ДНФ виконує наступне застосування закону подвійного заперечення:далі нижня риска згідно правила Де Моргана опускається на окремі висловлювання. Вираз під рискою приводить до вигляду ДНФ,після чого знову опускається риска на окремі висловлювання. Результат і буде КНФ 2) ДНФ перетворити до вигляду КНФ за дистрибутивною ознакою А \/ ВС=(А\/В) (А\/С) 3) Нехай деяка формула Р має вигляд ДНФ знаходимо для неї двоїсту формулу р* та приводить до ДНФ позначають її як а* після цього знаходимо формулу,що є двоїстою до (а*)*=а вона і буде КНФ при чому згідно принципу двоїстості А=Р
Приклад. Привести до КНФ функцію,задану в ДНФ:
f(x,y,z) = x
Використовуємо закон де Моргана, розкривши потім дужки і видаляючи зайві коньюнкції, отримаємо:
Використаємо до цього виразу закон Де Моргана отримаємо:
f(x,y,z) =
Це і є КНФ яку ми шукали для заданої функції.
40. Одержання мінімальних КНФ за допомогою диз'юнктивних форм. Приклад. Логічні функції, подані у ДНФ, після мінімізації можна перетворити в КНФ, використовуючи доведені нижче властивості логічних функцій. Припустимо, що дана логічна функція F = F(х1, х2,..., хn), яка приймає на наборах j1, j2, …, jm значення одиниці, а на наборах i1, i2, …, ip, де p=2n-m - значення нуля. Тоді має місце така теорема. Теорема 1. Диз'юнкція всіх конституент одиниці Ki1 \/ Ki2 \/ … \/ Kip, що не входять до ДДНФ логічної функції F, є запереченням цієї функції: Ki1 \/ Ki2 \/ … \/ Kip= Теорема 2. КНФ логічної функції Р, одержана з мінімальної ДНФ функції Р після її перетворення за допомогою формул де Моргана, також Буде мінімальною. Комбінаторні задачі У комбінаториці є декілька задач, які вирішуються послідовно одна за одною. Перша з них спочатку формулює вимоги до класу комбінаторних конфігурацій, які потрібно побудувати. Доводиться, що хоча б одна гака конфігурація існує, незважаючи на те, що побудувати гаку конфігурацію може бути досить непросто. Тому інколи буває достатньо теоретичного доведення її існування. Після розв'язання першої задачі комбінаторики розв'язується не менш важлива друга - задача переліку комбінаторних об'єктів, які відповідають вихідним правилам їх побудови. Саме на розв'язання цієї задачі спрямовані сьогодні зусилля багатьох учених. Є досить багато задач, які так чи інакше стосуються цієї загальної задачі. Наприклад, до неї належить питання про кількість різних способів, якими можна розмістити групу студентів з 30 чоловік на 30 чи більше місцях, або про кількість способів проведення матчів з футболу між 10 різними командами? Далі на основі отриманих розв'язків конкретних задач з переліку комбінаторних об'єктів розв'язується третя задача комбінаторики - це її побудова. Наприклад, потрібно не лише підрахувати кількість можливих варіантів розподілу ЗО студентів на ЗО місцях, а й побудувати всі ці розподіли або деякі з них у вигляді їх комбінаторних конфігурацій. Також може виникнути потреба побудувати таблицю матчів між 10 футбольними командами, а не тільки знати їх кількість. Четверта і остання задача комбінаторики - це задача про пошук серед комбінаторних конфігурацій такої, яка б приводила деяку функцію до оптимуму. Це на сьогодні досить нелегка для розв'язання загальна задача. Вона містить задачі комбінаторної оптимізації, наприклад, задачу комівояжера, яка на сьогодні ще не має остаточного розв'язання, хоча на її грунті сформульований клас складних переборних задач. 42. Основне правило комбінаторики. Приклади. Правило Добутку використовується тоді, коли кожний елемент множини А може бути вибраний разом з елементом множини В. Відповідно до кожного способу вибору елемента множини А буде зіставлятися к способів вибору елемента множини В. Тоді загальна кількість способів сумісного вибору елементів множини А з елементами множини В, очевидно, дорівнюватиме т* k. Модель урн можна застосувати і для ілюстрації правила Добутку. У цьому випадку розглядаються дві урни, у першій з яких знаходиться т куль, а в другій k. Будемо вважати, що будь-якій кулі першої урни може відповідати будь-яка куля з другої урни. А оскільки в першій урні знаходиться т куль, то й кількість способів вибору куль з першої урни разом з різними кулями з другої урни буде дорівнювати т-k. У загальному вигляді правило Добутку буде мати такий вигляд. Якщо треба виконати якусь дію, що може бути виконана к сумісними діями, перша з яких може бути виконана n1 способами, друга – п2і т.д. до k - ої дії, яку можна виконати пk способами, то основна дія може бути виконана М способами, де У цьому правилі важливу роль відіграє сполучник і, який об'єднує різні дії в одну. Приклад 2. На денне чергування в студентському гуртожитку вибирається два студента - один студент з трьох, що проживають у кімнаті 1, і один студент з чотирьох, які проживають у кімнаті 2. Скільки існує можливих способів формування різних пар з двохстудентів для чергування? Розв'язання. Кількість способів чергувань двох студентів з різних кімнат відповідно до правила Добутку буде дорівнювати 12. 43. Невпорядковані множини. Сполучення. Приклади. Сполученнями Порядок елементів в довільній kелементній підмножині не має значення. Два сполучення вважаються різними,якщо вони відрізняються один від одного хоча б одним елементом. Загальна кількість таких сполучень визначається як
де символом n позначаються добуток натуральних чисел від 1 до заданого натурального числаn включно. Зручно вважати,що 0!=1 Для сполучення має місце формула яку називається формулою симетрії і використовується коли k>
Приклад. Потрібно вибрати у подарунок 4 із 10 даних книжок. Скількома способами можна це зробити? Розв’язання:
44. Впорядковані множини. Перестановки. Приклади. Впорядковані множини – це скінчені множини, для яких є істотнім порядок елементів. У відповідність кожному елементу множини можна поставити натуральне число. Наприклад, числові послідовності – впорядковані множини, А множина яблук на дереві – не є впорядкована множина. Для позначення впорядкованих множин використовують круглі дужки, а невпорядкованих - фігурні. Перестановка – це будь-яка впорядкована множина з n елементів. Перестановки відрізняють між собою порядком елементів. Наприклад, з множини А={0,1,2} можна утворити шість перестановок: (0,1,2), (1,2,0), (2,0,1), (0,2,1), (1,0,2), (2,1,0). Задача 1. Задача 2. 45. Впорядковані підмножини. Розміщення. Приклади. Розміщення. Будь-яка впорядкована підмножина з m елементів даної множини М, яка містить n елементів, де Задача 3. 46. Перестановки з повторенням. Приклади. Розглянемо мультимножину M, а саме множину, яка може вміщувати однакові елементи. Наприклад,
Такі перестановки називають перестановками з повторенням. Практично, це перестановки елементів деякої мультимножини. Нехай, наприклад, У загальному випадку число перестановок мультимножини (перестановок з повторенням) буде рівне
Приклад 9. Скільки існує різних перестановок букв в слові "математика"?
47. Сполучення з повторенням. Приклади.
Приклад. Якщо у продажу є квіти чотирьох сортів, то різних букетів, що складаються з 7 квіток, можна скласти
48. Біном Ньютона. Біноміальні коефіцієнти. Біноміальна теорема. Трикутник Паскаля. ТрикутникПаскаля
Двочлен а+b називають біномом. Приклад
Біноміальна система числення з двійковим алфавітом. Діапазон, обмеження, характеристики та властивості.
2. Кодотвірна функція біноміальної системи числення з двійковим алфавітом. Нумерація біноміальних чисел.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |







 ,
,  ,
,  , 0, 1}, де B - непорожня множина, над елементами якої визначені три операції:
, 0, 1}, де B - непорожня множина, над елементами якої визначені три операції: ("тоді і тільки тоді, коли"), імплікація
("тоді і тільки тоді, коли"), імплікація  ("отже"), складання по модулю два
("отже"), складання по модулю два  ("що виключає або»), штрих Шеффера
("що виключає або»), штрих Шеффера  , стрілка Пірсу
, стрілка Пірсу  та інші.
та інші.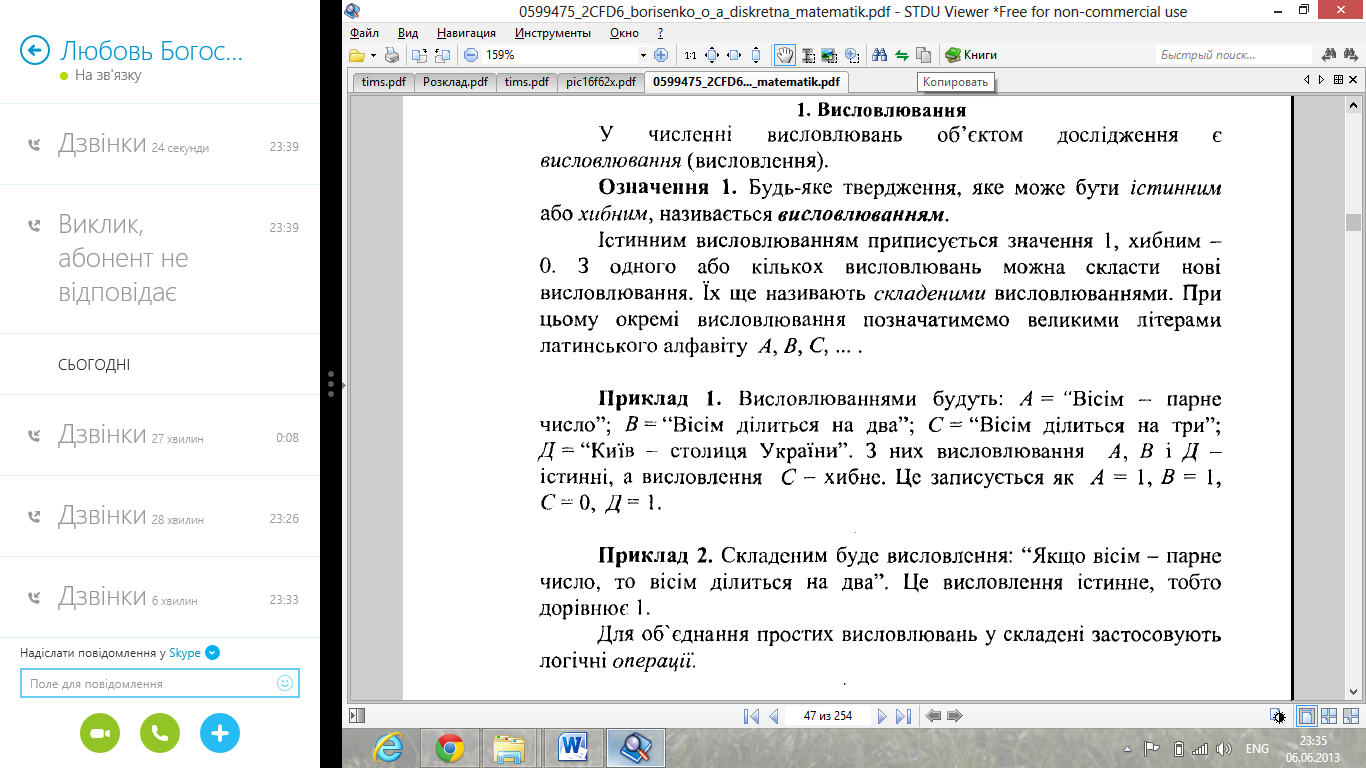







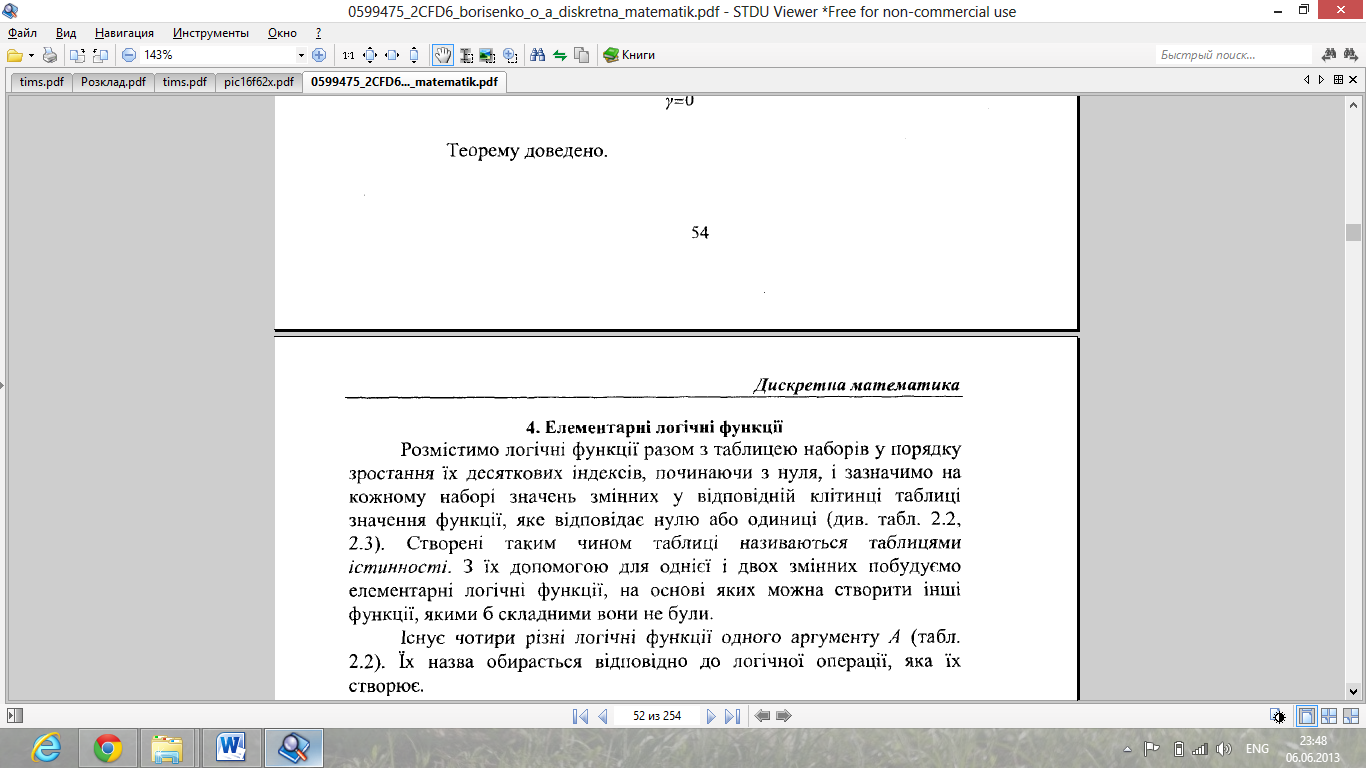






 ,
, 
 =
=  =х і
=х і 











 Для конкретної булевої функції карта Карно заповнюється таким чином. У клітках, що відповідні інтерпретаціям, на яких функція дорівнює одиниці, записують одиниці. Ці клітки відповідають конституентам одиниці, що присутні у ДДНФ функції. В інші клітки записують нулі.
Для конкретної булевої функції карта Карно заповнюється таким чином. У клітках, що відповідні інтерпретаціям, на яких функція дорівнює одиниці, записують одиниці. Ці клітки відповідають конституентам одиниці, що присутні у ДДНФ функції. В інші клітки записують нулі.



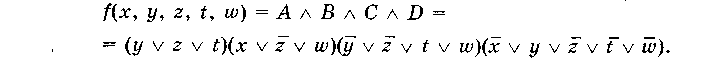
 Розв'язок. Складемо карту Карно для заданої функції (рис. 4.12).
Розв'язок. Складемо карту Карно для заданої функції (рис. 4.12). \/
\/  у\/х
у\/х 


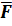
 називаються різні неупорядковані підмножини,що мають k елементів та побудовані з множинами М число елементів якої дорівнює n.
називаються різні неупорядковані підмножини,що мають k елементів та побудовані з множинами М число елементів якої дорівнює n. =
= 

 =
=  -формула симетрії
-формула симетрії =
=  =1
=1  =
= 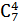


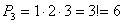

 , називається розміщенням з n елементів по m.
, називається розміщенням з n елементів по m.

 . Повторення елементів мультимножини можна задати і іншим способом
. Повторення елементів мультимножини можна задати і іншим способом  .
.  типів. Скільки існує перестановок
типів. Скільки існує перестановок  елементів першого типу,
елементів першого типу, 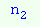 - другого типу і т.д.,
- другого типу і т.д.,  -
- 
 . Розглядаючи елементи M як різні, тобто
. Розглядаючи елементи M як різні, тобто  отримаємо
отримаємо  перестановок. Без індексів багато з перестановок будуть однакові. Фактично кожна з перестановки множини M зустрілась би рівно
перестановок. Без індексів багато з перестановок будуть однакові. Фактично кожна з перестановки множини M зустрілась би рівно  раз, оскільки для елементу 1 індекси можна поставити
раз, оскільки для елементу 1 індекси можна поставити 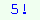 способами, елементу -
способами, елементу -  способами,елемента
способами,елемента  -
-  способами. Тому число перестановок множини М дорівнює
способами. Тому число перестановок множини М дорівнює 
 ,де
,де місць перестановки першого типу займають
місць перестановки першого типу займають 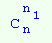 способами. Залишилось
способами. Залишилось  місць, на яких можна розмістити
місць, на яких можна розмістити  способами і т.д. елементи
способами і т.д. елементи  способами. За правилом прямого добутку
способами. За правилом прямого добутку 
 .
.