Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм одержання мінімальної КНФСодержание книги
Поиск на нашем сайте
1. Записують диз'юнкцію всіх конституент одиниці, які не входять до ДДНФ функції F, тобто знаходять F. 2. Знаходять мінімальну ДНФ за відомим алгоритмом для функції F. 3. Беруть заперечення від функції F і перетворюють її за правилами де Моргана в КНФ. Одержана КНФ буде мінімальною КНФ функції F. Приклад 1. Знайти мінімальну КНФ логічної функції F=F(А, В, С) = Розв'язування. 1. Знайдемо ДДНФ функції F: F = 2. Одержимо ДДНФ функції 3. Знайдемо скорочену ДНФ функції F, виконавши всі операції неповного склеювання і поглинання: 4. Складемо імплікантну матрицю для функції 5. Знайдемо мінімальні форми функції 6. Взявши заперечення від обох частин останніх рівностей і застосо- вуючи формули де Моргана, одержимо дві мінімальні кон'юнктивні нормальні форми:
41. Комбінаторика як розділ дискретної математики. Об'єкт дослідження комбінаторики. Комбінаторні задачі.
Під комбінаторикою звичайно розуміють розділ дискретної математики, присвячений розв'язанню задач про вибір та розміщення елементів скінченної множини згідно із заданими правилами. У результаті створюються необхідні комбінаторні об'єкти чи конфігурації. Характерними властивостями цих об'єктів є те, що вони відповідають деяким обмеженням щодо них, і тому завжди можна розпізнати дозволений комбінаторний об'єкт, який відповідає правилам його побудови, і недозволений, який не відповідає цим правилам. Комбінаторні задачі У комбінаториці є декілька задач, які вирішуються послідовно одна за одною. Перша з них спочатку формулює вимоги до класу комбінаторних конфігурацій, які потрібно побудувати. Доводиться, що хоча б одна гака конфігурація існує, незважаючи на те, що побудувати гаку конфігурацію може бути досить непросто. Тому інколи буває достатньо теоретичного доведення її існування. Після розв'язання першої задачі комбінаторики розв'язується не менш важлива друга - задача переліку комбінаторних об'єктів, які відповідають вихідним правилам їх побудови. Саме на розв'язання цієї задачі спрямовані сьогодні зусилля багатьох учених. Є досить багато задач, які так чи інакше стосуються цієї загальної задачі. Наприклад, до неї належить питання про кількість різних способів, якими можна розмістити групу студентів з 30 чоловік на 30 чи більше місцях, або про кількість способів проведення матчів з футболу між 10 різними командами?
Далі на основі отриманих розв'язків конкретних задач з переліку комбінаторних об'єктів розв'язується третя задача комбінаторики - це її побудова. Наприклад, потрібно не лише підрахувати кількість можливих варіантів розподілу ЗО студентів на ЗО місцях, а й побудувати всі ці розподіли або деякі з них у вигляді їх комбінаторних конфігурацій. Також може виникнути потреба побудувати таблицю матчів між 10 футбольними командами, а не тільки знати їх кількість. Четверта і остання задача комбінаторики - це задача про пошук серед комбінаторних конфігурацій такої, яка б приводила деяку функцію до оптимуму. Це на сьогодні досить нелегка для розв'язання загальна задача. Вона містить задачі комбінаторної оптимізації, наприклад, задачу комівояжера, яка на сьогодні ще не має остаточного розв'язання, хоча на її грунті сформульований клас складних переборних задач. 42. Основне правило комбінаторики. Приклади. Правило Добутку використовується тоді, коли кожний елемент множини А може бути вибраний разом з елементом множини В. Відповідно до кожного способу вибору елемента множини А буде зіставлятися к способів вибору елемента множини В. Тоді загальна кількість способів сумісного вибору елементів множини А з елементами множини В, очевидно, дорівнюватиме т* k. Модель урн можна застосувати і для ілюстрації правила Добутку. У цьому випадку розглядаються дві урни, у першій з яких знаходиться т куль, а в другій k. Будемо вважати, що будь-якій кулі першої урни може відповідати будь-яка куля з другої урни. А оскільки в першій урні знаходиться т куль, то й кількість способів вибору куль з першої урни разом з різними кулями з другої урни буде дорівнювати т-k. У загальному вигляді правило Добутку буде мати такий вигляд. Якщо треба виконати якусь дію, що може бути виконана к сумісними діями, перша з яких може бути виконана n1 способами, друга – п2і т.д. до k - ої дії, яку можна виконати пk способами, то основна дія може бути виконана М способами, де У цьому правилі важливу роль відіграє сполучник і, який об'єднує різні дії в одну.
Приклад 2. На денне чергування в студентському гуртожитку вибирається два студента - один студент з трьох, що проживають у кімнаті 1, і один студент з чотирьох, які проживають у кімнаті 2. Скільки існує можливих способів формування різних пар з двохстудентів для чергування? Розв'язання. Кількість способів чергувань двох студентів з різних кімнат відповідно до правила Добутку буде дорівнювати 12. 43. Невпорядковані множини. Сполучення. Приклади. Сполученнями Порядок елементів в довільній kелементній підмножині не має значення. Два сполучення вважаються різними,якщо вони відрізняються один від одного хоча б одним елементом. Загальна кількість таких сполучень визначається як
де символом n позначаються добуток натуральних чисел від 1 до заданого натурального числаn включно. Зручно вважати,що 0!=1 Для сполучення має місце формула яку називається формулою симетрії і використовується коли k>
Приклад. Потрібно вибрати у подарунок 4 із 10 даних книжок. Скількома способами можна це зробити? Розв’язання:
44. Впорядковані множини. Перестановки. Приклади. Впорядковані множини – це скінчені множини, для яких є істотнім порядок елементів. У відповідність кожному елементу множини можна поставити натуральне число. Наприклад, числові послідовності – впорядковані множини, А множина яблук на дереві – не є впорядкована множина. Для позначення впорядкованих множин використовують круглі дужки, а невпорядкованих - фігурні. Перестановка – це будь-яка впорядкована множина з n елементів. Перестановки відрізняють між собою порядком елементів. Наприклад, з множини А={0,1,2} можна утворити шість перестановок: (0,1,2), (1,2,0), (2,0,1), (0,2,1), (1,0,2), (2,1,0). Задача 1. Задача 2. 45. Впорядковані підмножини. Розміщення. Приклади. Розміщення. Будь-яка впорядкована підмножина з m елементів даної множини М, яка містить n елементів, де Задача 3. 46. Перестановки з повторенням. Приклади. Розглянемо мультимножину M, а саме множину, яка може вміщувати однакові елементи. Наприклад,
Такі перестановки називають перестановками з повторенням. Практично, це перестановки елементів деякої мультимножини. Нехай, наприклад,
У загальному випадку число перестановок мультимножини (перестановок з повторенням) буде рівне
Приклад 9. Скільки існує різних перестановок букв в слові "математика"?
47. Сполучення з повторенням. Приклади.
Приклад. Якщо у продажу є квіти чотирьох сортів, то різних букетів, що складаються з 7 квіток, можна скласти
48. Біном Ньютона. Біноміальні коефіцієнти. Біноміальна теорема. Трикутник Паскаля. ТрикутникПаскаля
Двочлен а+b називають біномом. Приклад
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.176.25 (0.008 с.) |

 називаються різні неупорядковані підмножини,що мають k елементів та побудовані з множинами М число елементів якої дорівнює n.
називаються різні неупорядковані підмножини,що мають k елементів та побудовані з множинами М число елементів якої дорівнює n. =
= 

 =
=  -формула симетрії
-формула симетрії =
=  =1
=1  =
= 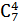


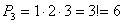

 , називається розміщенням з n елементів по m.
, називається розміщенням з n елементів по m.

 . Повторення елементів мультимножини можна задати і іншим способом
. Повторення елементів мультимножини можна задати і іншим способом  .
.  типів. Скільки існує перестановок
типів. Скільки існує перестановок  елементів першого типу,
елементів першого типу, 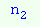 - другого типу і т.д.,
- другого типу і т.д.,  -
- 
 . Розглядаючи елементи M як різні, тобто
. Розглядаючи елементи M як різні, тобто  отримаємо
отримаємо  перестановок. Без індексів багато з перестановок будуть однакові. Фактично кожна з перестановки множини M зустрілась би рівно
перестановок. Без індексів багато з перестановок будуть однакові. Фактично кожна з перестановки множини M зустрілась би рівно  раз, оскільки для елементу 1 індекси можна поставити
раз, оскільки для елементу 1 індекси можна поставити 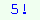 способами, елементу -
способами, елементу -  способами,елемента
способами,елемента  -
-  способами. Тому число перестановок множини М дорівнює
способами. Тому число перестановок множини М дорівнює 
 ,де
,де місць перестановки першого типу займають
місць перестановки першого типу займають 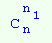 способами. Залишилось
способами. Залишилось  місць, на яких можна розмістити
місць, на яких можна розмістити  способами і т.д. елементи
способами і т.д. елементи  способами. За правилом прямого добутку
способами. За правилом прямого добутку 
 .
.