
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості інтеграла Лебега у загальному випадкуСодержание книги
Поиск на нашем сайте
1. Довільна скінченна функція Доведення. На підставі теореми 5.1.1 існує послідовність простих функцій 2. Довільна вимірна і обмежена на множині Доведення. На підставі теореми 5.1.1 існує послідовність простих функцій
3. Якщо функція Доведення. За означенням 5.2.1 існує послідовність простих інтегровних функцій 4. Якщо функція
Доведення. За означенням 5.2.1 існує послідовність простих інтегровних функцій
5. Якщо функції
Доведення. За означенням 5.2.1 існує послідовність простих інтегровних функцій
6. Якщо на множині
Доведення. На підставі теореми 5.1.1 існує послідовність простих функцій
За означенням 5.2.1 існує послідовність простих інтегровних функцій
Із нерівностей (5.2.2) - (5.2.3) і умови
Отже прості функції
Спрямувавши Наслідок 5.2.1 Для того щоб вимірна функція Дійсно, якщо функція Якщо функція 7. Адитивність інтеграла Лебега. Нехай функція
і, якщо справа маємо ряд, то він збігається абсолютно. Доведення. На підставі означення інтегрованості функції
Завдяки довільності
8. Нехай
то функція Доведення. На підставі означення інтегрованості функції
На підставі властивості 11 інтеграла від простої функції, функція 9. Абсолютна неперервність інтеграла Лебега. Нехай функція
Доведення. Розглянемо спочатку випадок обмеженої функції:
Нехай тепер
Знайдемо натуральне число
10. Нерівність Чебишева. Для довільної інтегрованої на множині
Доведення. На підставі адитивності інтеграла Лебега маємо
Наслідок 5.2.2. (Наслідок з нерівності Чебишева). Якщо для інтегрованої на множині
то Доведення. Застосуємо нерівність Чебишева для константи
і зобразимо множину
Так як кожна множина 11. Інтеграли Лебега від еквівалентних функцій. Якщо функції Доведення. Розглянемо різницю інтегралів і використовуємо адитивність інтеграла і рівність нулю інтеграла Лебега по будь-якій множині міри нуль:
Одержана властивість показує, що якщо у скінченної інтегрованої функції Означення 5.2.3. Вимірнаі майже скрізь скінченна на множині Очевидно, що усі властивості інтеграла Лебега для функцій, що приймають скінченні значення, мають місце і для майже скрізь скінченних.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.230.81 (0.009 с.) |

 на множині
на множині  міри нуль інтегровна і
міри нуль інтегровна і 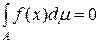 .
. , що рівномірно збігається на множені
, що рівномірно збігається на множені  , якщо
, якщо  .
.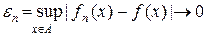 . Із нерівності
. Із нерівності 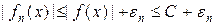 випливає інтегровність простих функцій
випливає інтегровність простих функцій 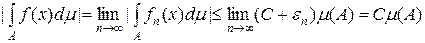 .
.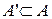 .
.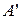 .
.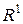 інтегровна за Лебегом функція l
інтегровна за Лебегом функція l  .
. рівномірно збігається і на множині
рівномірно збігається і на множині 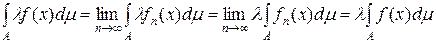 .
. інтегровні за Лебегом на множині
інтегровні за Лебегом на множині  .
.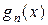 , що рівномірно збігається на множені
, що рівномірно збігається на множені 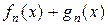 рівномірно збігається на множені
рівномірно збігається на множені 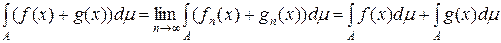 .
. £
£ 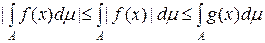 . (5.2.1)
. (5.2.1)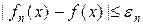 випливає
випливає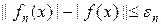 ,
,  . (5.2.2)
. (5.2.2)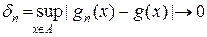 . Із нерівності
. Із нерівності  випливає
випливає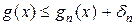 . (5.2.3)
. (5.2.3)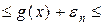
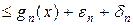 .
.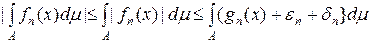 .
.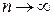 , одержимо (5.2.1).
, одержимо (5.2.1). рівномірно збігається на множені
рівномірно збігається на множені  виконуються умови властивості 6. Отже функція
виконуються умови властивості 6. Отже функція  деяке розбиття множини
деяке розбиття множини 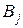 . Тоді
. Тоді (5.2.4)
(5.2.4)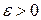 знайдеться проста інтегровна функція
знайдеться проста інтегровна функція 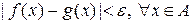 . Для функції
. Для функції 
 .
.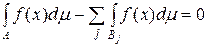 . Абсолютна збіжність ряду (5.2.4) випливає з нерівностей:
. Абсолютна збіжність ряду (5.2.4) випливає з нерівностей: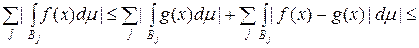
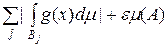 .
.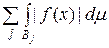 ,
,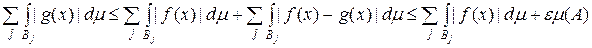 .
. таке, що для довільної вимірної підмножини
таке, що для довільної вимірної підмножини  , міра якої
, міра якої  , виконується нерівність
, виконується нерівність .
. . На підставі властивості 2 для довільної вимірної підмножини
. На підставі властивості 2 для довільної вимірної підмножини  .
. , де
, де  довільне натуральне число. В силу адитивності інтеграла Лебега
довільне натуральне число. В силу адитивності інтеграла Лебега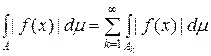 .
.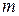 таке, що
таке, що  , позначимо через
, позначимо через 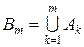 і покладемо
і покладемо 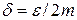 . Тоді
. Тоді  і на підставі властивості 2 і вибору числа
і на підставі властивості 2 і вибору числа 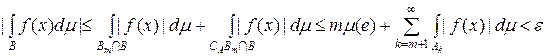 .
.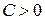 має місце нерівність
має місце нерівність .
. .
.
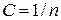 , де
, де  довільне натуральне число
довільне натуральне число
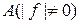 у вигляді
у вигляді .
.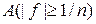 має міру нуль, то і міра об’єднання дорівнює нулю.
має міру нуль, то і міра об’єднання дорівнює нулю.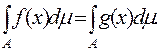
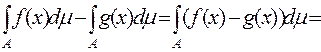

 .
.


