
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття множини, операції над множинамиСодержание книги
Поиск на нашем сайте
Означення 1.1.1. Множиною називається сукупність, набір, сім’я, збори, колекція предметів, вибраних по деякому правилу (закону), або просто указаних; при цьому усі предмети різні. Предмети, із яких складається множина називаються елементами. Множини будемо позначати прописними латинськими буквами, а елементи – малими літерами. Якщо елемент a належить множині A, то це будимо записувати так: а Î А. Приклади. 1. 2. Сегмент 3.
Якщо кожен елемент множини А є елементом множини В, то будемо казати, що множина А міститься в множині В, або множина В містить множину А і позначати це будемо так: А Ì В, або В É А. Будемо також казати, що множина А є підмножиною множини В. Наприклад, Якщо кожен елемент множини А є елементом множини В і навпаки кожен елемент множини В є елементом множини А, то множини рівні: А = В. Отже, щоб довести, що множини А і В рівні треба показати, що А Ì В і В Ì А. Означення 1.1.2. Нехай задана деяка сім’я множин: Якщо маємо дві множини А і В, то їх об’єднання позначимо через Означення 1.1.3. Перетином множин сім’я Позначення перетину: перетин сім’ї множин - Означення 1.1.4. Різницею множини А і В називається множина усіх елементів множини А, що не належать множині В. Різниця множин А і В позначається таким чином: А \ В. Означення 1.1.5. Симетричною різницею множини А і В називається множина Означення 1.1.6. Якщо множина В є підмножиною множини А, то різниця множин А і В називається доповнення множини В до множини А. Доповнення множини В до множини А позначається символом Властивості об’єднання, перетину і доповнення множин (властивості двоїстості). Теорема 1.1.1 (Співвідношення двоїстості). Нехай кожна із множини
Доведення. Нехай Задачі. 1. Довести, що 2. Довести, що 3. Довести, що 4. Довести, що 5. Довести, що 6. Довести, що 7. Довести, що 8. Довести, що 9. Довести, що 10. Довести, що 11. Довести, що 12. Довести, що 13. Верхня границя 14. Нижня границя
1.2. Поняття відображення і взаємно однозначначної відповідності Означення 1.2.1. Правило або закон, по якому кожному елементу а множини А ставиться у відповідність один елемент b множини В, називається функцією обо відображенням множини А в В. Функція звичайно позначається літерою латинського або грецького алфавіту, наприклад, Поряд з термінами «функція» і «відображення» будемо використовувати рівнозначні ім у деяких сітуаціях терміни «перетворення», «оператор», «відповідність». Означення 1.2.2. Взаємно однозначною відповідністю множин А і В називається відображення В цьому випадку прообраз
Задачі. 1. Нехай
2. Нехай
Означення 1.2.3. Якщо для множин А і В можливо указати взаємно однозначну відповідність, то множини А і В називається еквівалентними. Еквівалентність множин А і В позначається символом: А ~ В. Властивості еквівалентних множин: 1. А ~ А. 2. Якщо А ~ В, то В ~ А. Ця властивість називається транзитивністю. 3. Якщо множини
4. Нехай А ~ В, 5. Якщо А ~ В, З останньої рівності випливає що 6. Теорема 1.2.1 (Теорема Кантора-Бернштейна). Нехай підмножина Перед доведенням теореми Кантора-Бернштейна розглянемо лему, яка цікава сама по собі. Лема 1. 2.1. Якщо Доведення. Нехай Далі, внаслідок властивості 5 еквівалентних множин,
і в загальному випадку:
Нехай
і
Тепер зауважимо, що
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.19.206 (0.008 с.) |

 множина усіх натуральних чисел,
множина усіх натуральних чисел,  множина всіх цілих чисел,
множина всіх цілих чисел, 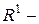 множина всіх дійсних чисел,
множина всіх дійсних чисел, 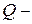 множина всіх раціональних чисел.
множина всіх раціональних чисел. множина всіх дійсних чисел
множина всіх дійсних чисел 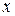 , що задовольняють умову
, що задовольняють умову  , інтервал
, інтервал  множина всіх дійсних чисел
множина всіх дійсних чисел  , півінтервал
, півінтервал 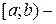 множина всіх дійсних чисел
множина всіх дійсних чисел  , півінтервал
, півінтервал  множина всіх дійсних чисел
множина всіх дійсних чисел  .
. множина усіх функцій заданих і неперервних на сегменті
множина усіх функцій заданих і неперервних на сегменті 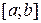 ,
,  множина всіх функцій заданих і обмежених на сегменті
множина всіх функцій заданих і обмежених на сегменті  ,
,  .
. . Множина всіх елементів, що належать хоч би однієї із множин даної сім’ї, називається об’єднанням множин
. Множина всіх елементів, що належать хоч би однієї із множин даної сім’ї, називається об’єднанням множин  і позначається об’єднання так
і позначається об’єднання так 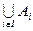 .
. . Якщо множин n штук:
. Якщо множин n штук:  , то позначення їх об’єднання буде
, то позначення їх об’єднання буде  , або
, або  .
. , перетин двох множин -
, перетин двох множин - 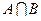 , перетин n множин -
, перетин n множин -  , або
, або 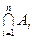 . Якщо множини не мають спільних елементів, то будемо казати, що їх перетин – порожня множина. Порожню множину будемо позначати символом Æ. Порожня множина може бути не тільки результатом перетину. Наприклад: множина дійсних розв’язків рівняння
. Якщо множини не мають спільних елементів, то будемо казати, що їх перетин – порожня множина. Порожню множину будемо позначати символом Æ. Порожня множина може бути не тільки результатом перетину. Наприклад: множина дійсних розв’язків рівняння  – порожня множина.
– порожня множина.
 . Різниця позначається так:
. Різниця позначається так:  .
. .
.
 тобто
тобто  і
і  , отже
, отже  для кожного
для кожного  і
і  . Навпаки, нехай
. Навпаки, нехай  і
і  для кожного
для кожного  .
. .
. .
. .
. тоді і тільки тоді, коли
тоді і тільки тоді, коли  .
. .
. .
. .
. , якщо
, якщо  і множини
і множини  не перетинаються.
не перетинаються. .
. .
. послідовності
послідовності  є множина
є множина  . Довести, що
. Довести, що  послідовності
послідовності  . Довести, що
. Довести, що  і писати
і писати  , або
, або  , при цьому елемент
, при цьому елемент  називається образом елементу
називається образом елементу 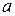 , а елемент
, а елемент  називається образом множини
називається образом множини  і позначається символом
і позначається символом  . Якщо при перетворенні
. Якщо при перетворенні  є образом деякого елементу
є образом деякого елементу  то кажуть, що
то кажуть, що  , або
, або 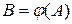 . Множина
. Множина  називається прообразом множини
називається прообразом множини  і позначається символом
і позначається символом 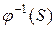 .
. кожної одно елементної множини
кожної одно елементної множини 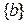 є відображення множини В на А, яке теж є взаємно однозначною відповідністю. Відображення
є відображення множини В на А, яке теж є взаємно однозначною відповідністю. Відображення  і
і  називаються взаємно оберненими.
називаються взаємно оберненими. ,
,  і
і  . Доведіть наступні співвідношення:
. Доведіть наступні співвідношення: ,
, ,
, .
. і
і  . Доведіть наступні співвідношення:
. Доведіть наступні співвідношення: ,
,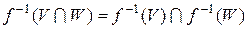 ,
, .
.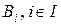 теж попарно не перетинаються і для будь якого
теж попарно не перетинаються і для будь якого  ~
~  , то
, то ~
~  .
. -довільна підмножина множини А, то
-довільна підмножина множини А, то  .
.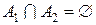 ,
,  і
і 

 , якщо
, якщо  , тобто
, тобто  ~
~  . Дійсно,
. Дійсно,  і
і  Отже
Отже  еквівалентна множині
еквівалентна множині  , а підмножина
, а підмножина  множини
множини  еквівалентна множині
еквівалентна множині  . Тоді
. Тоді  .
. і
і  . Тоді
. Тоді  .
. взаємно однозначне перетворення множини
взаємно однозначне перетворення множини 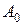 на
на  . Покладемо
. Покладемо  . З умови леми і означення множин
. З умови леми і означення множин  випливає їх монотонність:
випливає їх монотонність:  . Дійсно, для
. Дійсно, для  ,
,  це умова леми. Припустимо, що
це умова леми. Припустимо, що  , якщо
, якщо 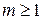 . Тоді
. Тоді  , тобто
, тобто  .
.

 . Оскільки
. Оскільки  (1.1.1)
(1.1.1) . (1.1.2)
. (1.1.2)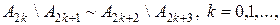 і доданки у правих частинах рівностей (1.1.1) - (1.1.2) попарно не перетинаються. Окрім того
і доданки у правих частинах рівностей (1.1.1) - (1.1.2) попарно не перетинаються. Окрім того  . Отже, внаслідок властивості 3 еквівалентних множин,
. Отже, внаслідок властивості 3 еквівалентних множин, 


