
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості відкритих і замкнених множинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Для того щоб множина Доведення. Необхідність. Нехай множина Достатність. Нехай множина 2. Об’єднання будь-якої сім’ї Доведення. Нехай 3. Перетин будь-якої сім’ї Доведення. Внаслідок співвідношень двоїстості і властивостей 1 і 2 множина 4. Перетин скінченного набора Доведення. Нехай 5. Об’єднання скінченного набора Доведення. В силу співвідношень двоїстості і властивостей 1 і 4 множина Покажемо на прикладах, що умова скінченнності у властивостей 3,4 не зайва. Приклад 1. Нехай Приклад 2. Нехай
Нехай Якщо Теорема 2.1.3 (Структура відкритої обмеженої множина з простору Доведення. Нехай Покажемо, що складових інтервалів не більш ніж зчисленна множина. Для цього виберемо по раціональній точці з кожного інтервала. Оскільки інтервали не перетинаються, то ці точки різні і тому утворюють деяку підмножину Теорема доведена. Теорема 2.1.4 (Структура замкненої обмеженої множина з простору Доведення. Якщо Теорема доведена. Із означень досконалої множини і ізольованої точки внаслідок теореми 2.1.4 очевидно випливає наступне твердження. Теорема 2.1.5 Для того щоб замкнена обмежена множина
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.45.144 (0.007 с.) |

 була відкритою необхідно і достатньо, щоб доповнення (доповнення до
була відкритою необхідно і достатньо, щоб доповнення (доповнення до 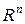 ) було замкнуто.
) було замкнуто. відкрита і припустимо, що
відкрита і припустимо, що  не містить граничну точку
не містить граничну точку 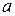 . Тоді
. Тоді  і отже існує окіл
і отже існує окіл  такий, що
такий, що  , а це означає, що
, а це означає, що 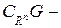 замкнена і точка
замкнена і точка  . Тоді існує окіл
. Тоді існує окіл  відкрита, що і треба було довести.
відкрита, що і треба було довести.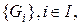 відкритих множин є множина відкрита.
відкритих множин є множина відкрита. . Тоді
. Тоді  і існує окіл точки
і існує окіл точки 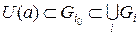 . Отже множина
. Отже множина  відкрита.
відкрита. замкнутих множин є множина замкнута.
замкнутих множин є множина замкнута. відкрита, отже (властивість 1)
відкрита, отже (властивість 1)  замкнена.
замкнена.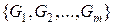 відкритих множин є множина відкрита.
відкритих множин є множина відкрита.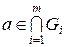 . Тоді для кожної множини
. Тоді для кожної множини 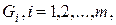 знайдеться окіл
знайдеться окіл  . Покладемо
. Покладемо  . Очевидно, що для будь-якого
. Очевидно, що для будь-якого  :
:  і
і 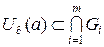 .
. замкнених множин є множина замкнена.
замкнених множин є множина замкнена. відкрита, отже (властивість 1)
відкрита, отже (властивість 1)  замкнена.
замкнена. . Тоді
. Тоді  множина і не відкрита і не замкнена.
множина і не відкрита і не замкнена. . Тоді
. Тоді  множина і не відкрита і не замкнена.
множина і не відкрита і не замкнена. є довільної, обмеженою знизу, замкненою множиною з простору
є довільної, обмеженою знизу, замкненою множиною з простору 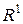 і
і  . Внаслідок означення точної нижньої межі для будь-якого натурального числа
. Внаслідок означення точної нижньої межі для будь-якого натурального числа  знайдеться елемент
знайдеться елемент 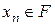 такий, що
такий, що  . Якщо серед елементів
. Якщо серед елементів  існує нескінченна множини різних, то точка
існує нескінченна множини різних, то точка  є граничною точкою множини
є граничною точкою множини  таке, що для всіх
таке, що для всіх 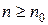 елементи
елементи  , отже
, отже  . Аналогічно, якщо
. Аналогічно, якщо  , то
, то  .
. , а сегмент
, а сегмент  називається найменшим сегментом, що містить замкнену множину
називається найменшим сегментом, що містить замкнену множину 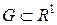 є об’єднання скінченної або зчисленної множини попарно неперетинних інтервалів
є об’єднання скінченної або зчисленної множини попарно неперетинних інтервалів 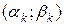 , кінці яких не належать множині
, кінці яких не належать множині  обмежена знизу і замкнена. Тому
обмежена знизу і замкнена. Тому 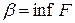 належить
належить 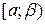 належить
належить  обмежена зверху і замкнена. Тому
обмежена зверху і замкнена. Тому  належить
належить  належить
належить 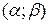 належить
належить  , що мають спільну точку
, що мають спільну точку 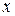 , і нехай
, і нехай 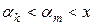 . Тоді точка
. Тоді точка  і через те належить множині
і через те належить множині  складовий.
складовий. множини раціональних чисел. Таким чином установлена взаємно однозначна відповідність між множиною складових інтервалів множини
множини раціональних чисел. Таким чином установлена взаємно однозначна відповідність між множиною складових інтервалів множини  є або сегментом
є або сегментом  . Розглянемо
. Розглянемо  . Очевидно, що
. Очевидно, що 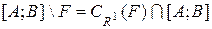 . Оскільки точки
. Оскільки точки  , то
, то  . Отже множина
. Отже множина  є відкритою і за теоремою 2.1.3 ії можно зобразити у вигляді
є відкритою і за теоремою 2.1.3 ії можно зобразити у вигляді 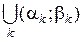 не більш ніж зчисленної множини попарно неперетинних інтервалів. Тоді
не більш ніж зчисленної множини попарно неперетинних інтервалів. Тоді  .
. не були кінцями інтервалів
не були кінцями інтервалів 


