Граничний перехід у класі вимірних функцій
Теорема 4.1.2 Границя  послідовності вимірних функцій послідовності вимірних функцій  , що збігається у кожній точки множина , що збігається у кожній точки множина  ,- вимірна. ,- вимірна.
Доведення. Для будь-яких натуральних чисел 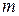 , ,  і довільного числа і довільного числа 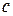 розглянемо вимірну множину розглянемо вимірну множину  . Теорема буде доведена, якщо одержимо рівність . Теорема буде доведена, якщо одержимо рівність
 . .
Нехай елемент  , тобто , тобто 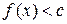 . Знайдемо натуральне число . Знайдемо натуральне число  таке, що таке, що  , а потім, використовуючи властивості границі, знайдемо таке натуральне число , а потім, використовуючи властивості границі, знайдемо таке натуральне число  , починаючи з якого , починаючи з якого  . Тоді елемент . Тоді елемент  і отже належить правої частини. Навпаки, якщо елемент і отже належить правої частини. Навпаки, якщо елемент  , то знайдуться натуральні числа , то знайдуться натуральні числа  і і  такі, що такі, що  , тобто , тобто  до усіх до усіх  . Переходячи в останній нерівності до границі, коли . Переходячи в останній нерівності до границі, коли  , дістанемо , дістанемо

і отже 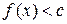 . Рівність множин установлена і теорема доведена. . Рівність множин установлена і теорема доведена.
Означення 4.1.3. Деяка обставина (твердження, властивість, умова) має місце майже скрізь на множині  , якщо вона має місце для усіх елементів множини , якщо вона має місце для усіх елементів множини  , окрім елементів підмножини , окрім елементів підмножини 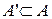 , міра якої дорівнює нулю. , міра якої дорівнює нулю.
Означення 4.1.4. Функції  і і  , задані і вимірні на множині , задані і вимірні на множині  , називаються еквівалентними, якщо вони майже скрізь збігаються на множені , називаються еквівалентними, якщо вони майже скрізь збігаються на множені  , тобто , тобто  . .
Еквівалентність функцій  і і  будемо позначати символом будемо позначати символом 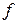 ~ ~  . .
Означення 4.1.5. Функція  називається майже скрізь скінченною, якщо називається майже скрізь скінченною, якщо 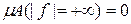 . .
Означення 4.1.6. Послідовність вимірних на множині  функцій функцій  збігається майже скрізь до функції збігається майже скрізь до функції  , якщо вона збігається у всіх точках множини , якщо вона збігається у всіх точках множини  , крім точок підмножини , крім точок підмножини 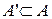 , міра якої дорівнює нулю. , міра якої дорівнює нулю.
Теорема 4.1.3 (Узагальнення теореми 4.1.2) Якщо послідовність майже скрізь скінченних вимірних функцій  збігається майже скрізь на множині збігається майже скрізь на множині  до майже скрізь скінченної функції до майже скрізь скінченної функції  , то , то  - вимірна. - вимірна.
Доведення. Нехай 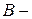 підмножина тих елементів множини підмножина тих елементів множини  , де функції , де функції  і і  приймають нескінченні значення і послідовність функцій приймають нескінченні значення і послідовність функцій  не збігається до не збігається до  . За умовою теореми підмножина . За умовою теореми підмножина  має міру нудь, отже на підставі властивості 1, має міру нудь, отже на підставі властивості 1,  вимірна на вимірна на  . У кожній точки вимірній множині . У кожній точки вимірній множині  послідовність скінченних вимірних функцій послідовність скінченних вимірних функцій  збігається до скінченної функції збігається до скінченної функції  , отже , отже  є вимірною і на множені є вимірною і на множені  . Завдяки властивості 4 функція . Завдяки властивості 4 функція  вимірна на вимірна на  . .
Означення 4.1.7. Послідовність вимірних на множині  функцій функцій  збігається за мірою до функції збігається за мірою до функції  , якщо для будь-якого , якщо для будь-якого 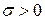 міра множини міра множини  прямує до нуля, коли прямує до нуля, коли 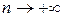 . При цьому у множину . При цьому у множину  включаються і ті елементи, у яких включаються і ті елементи, у яких  і і  приймають нескінченні значення. приймають нескінченні значення.
Теорема 4.1.4 (Теорема Лебега). Якщо послідовність майже скрізь скінченних вимірних функцій  збігається майже скрізь на множині збігається майже скрізь на множині  до майже скрізь скінченної функції до майже скрізь скінченної функції  , то , то  збігається на множині збігається на множині  до до  за мірою. за мірою.
Доведення. Нехай 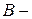 підмножина тих елементів множини підмножина тих елементів множини  , де функції , де функції  і і  приймають нескінченні значення і послідовність функцій приймають нескінченні значення і послідовність функцій  не збігається до не збігається до  . За умовою теореми підмножина . За умовою теореми підмножина  має міру нудь. Визначимо наступні множини має міру нудь. Визначимо наступні множини
 і і  . .
Множин  вимірні, вимірні,  . Тому, на підставі властивості 12 вимірних множин, . Тому, на підставі властивості 12 вимірних множин, 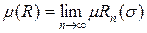 . Покажемо, що . Покажемо, що  . Нехай елемент . Нехай елемент 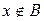 . Тоді в точці . Тоді в точці 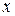 послідовність послідовність  збігається до збігається до  , отже для будь-якого , отже для будь-якого 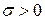 знайдеться число знайдеться число  таке, що для усіх таке, що для усіх  має місце нерівність має місце нерівність
 . .
Отже елемент 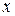 не належить множині не належить множині  , і тим паче перетину , і тим паче перетину  . Оскільки . Оскільки  , то і , то і  . Тому . Тому  , коли , коли 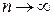 , але першим доданком об’єднання, що визначає , але першим доданком об’єднання, що визначає  , є множина , є множина  , отже , отже  , коли , коли 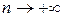 . .
Теорема доведена.
Теорема 4.1.5 Існують послідовності вимірних функцій  , що збігається за мірою до , що збігається за мірою до  , але не збігається ні в одній точки до жодної функції. , але не збігається ні в одній точки до жодної функції.
Доведення. До кожного натурального  розіб’ємо півінтервал розіб’ємо півінтервал  на на  неперетинних півінтервалів неперетинних півінтервалів  і визначимо групу з і визначимо групу з  функцій: функцій:

Функції  прості і тому вимірні на півінтервалі прості і тому вимірні на півінтервалі  . Запишемо функції в рядок . Запишемо функції в рядок  так, щоб функції з більшим верхнім індексом (з однієї групи) слідували за функцією з меншим індексом. Цю послідовність позначимо символом так, щоб функції з більшим верхнім індексом (з однієї групи) слідували за функцією з меншим індексом. Цю послідовність позначимо символом  . Очевидно, що . Очевидно, що  , де , де  Послідовність функцій Послідовність функцій  збігається за мірою до збігається за мірою до  . Дійсно, для будь-якого . Дійсно, для будь-якого 
 . .
Нехай 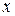 довільна точка з півінтервалу довільна точка з півінтервалу  . До кожного натурального . До кожного натурального  знайдеться індекс знайдеться індекс  такий, що такий, що  . Тоді . Тоді  , а всі інші функції з цієї групи в точці , а всі інші функції з цієї групи в точці 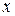 приймають значення нуль. Тому послідовність функцій приймають значення нуль. Тому послідовність функцій  не збігається ні в одній точці з півінтервалу не збігається ні в одній точці з півінтервалу  . .
Теорема 4.1.6 (Теорема Рісса). Якщо послідовність вимірних функцій  збігається за мірою на множині збігається за мірою на множині  до до  , то із неї можливо вилучити підпослідовність , то із неї можливо вилучити підпослідовність  , що збігається майже скрізь на множині , що збігається майже скрізь на множині  до до  . .
Доведення. Нехай монотонна послідовність невід’ємних чисел  прямує до нуля, а послідовність невід’ємних чисел прямує до нуля, а послідовність невід’ємних чисел 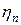 така, що ряд така, що ряд  збігається. Знайдемо натуральне число збігається. Знайдемо натуральне число  таке, що таке, що
 . .
Це можливо тому, що  прямує до нуля, коли прямує до нуля, коли 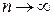 . За тією ж причиною знайдеться натуральне число . За тією ж причиною знайдеться натуральне число  таке, що таке, що  і і
 . .
Припустимо, що визначені числа  . Знайдемо натуральне число . Знайдемо натуральне число 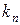 таке, що таке, що  і і
 . .
Покажемо, що підпослідовність  шукана. Для цього визначимо наступні множини шукана. Для цього визначимо наступні множини
 і і 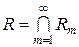 . .
Множин  вимірні, вимірні,  . Тому, на підставі властивості 12 вимірних множин, . Тому, на підставі властивості 12 вимірних множин,  . Завдяки вибору послідовності чисел . Завдяки вибору послідовності чисел 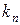

і оскільки ряд  збігається, то збігається, то 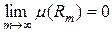 , отже , отже  . Тепер доведемо, що у кожній точці множини . Тепер доведемо, що у кожній точці множини  послідовність послідовність  збігається до збігається до  . Нехай . Нехай  , тоді , тоді  і отже знайдеться натуральне число і отже знайдеться натуральне число  таке, що таке, що  , тобто для усіх , тобто для усіх  елемент елемент  . Отже . Отже
 для усіх для усіх  . .
Оскільки  прямує до нуля, то прямує до нуля, то  збігається до збігається до  . .
Теорема доведена.
Теорема 4.1.7 (Теорема Єгорова). Якщо послідовність майже скрізь скінченних вимірних функцій  збігається майже скрізь на множині збігається майже скрізь на множині  до майже скрізь скінченної функції до майже скрізь скінченної функції  , то для будь-якого , то для будь-якого  існує вимірна множина існує вимірна множина  така, що така, що
1)  . .
2) На множині  послідовність функцій послідовність функцій  збігається рівномірно до функції збігається рівномірно до функції  . .
Доведення. Нехай  . При доведенні теореми Лебега було установлено, що для будь-якого . При доведенні теореми Лебега було установлено, що для будь-якого 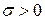 : :  , коли , коли 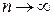 . .
Нехай монотонна послідовність невід’ємних чисел  прямує до нуля, а послідовність невід’ємних чисел прямує до нуля, а послідовність невід’ємних чисел 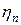 така, що ряд така, що ряд  збігається. Для кожного натурального числа збігається. Для кожного натурального числа 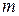 знайдемо натуральне число знайдемо натуральне число 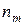 таке, що таке, що
 . .
Для будь-якого  знайдемо натуральне число знайдемо натуральне число  таке, що таке, що 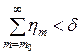 і покладемо і покладемо  . На підставі наслідку 5 із властивості 8 вимірних множин . На підставі наслідку 5 із властивості 8 вимірних множин
 , ,
отже  . Візьмемо довільне додатне число e і знайдемо таке натуральне число . Візьмемо довільне додатне число e і знайдемо таке натуральне число  , що , що 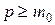 і і  . Це можливо тому, що . Це можливо тому, що  , коли , коли 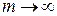 . Нехай . Нехай  , тоді , тоді 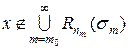 і отже і отже  . Внаслідок означення множини . Внаслідок означення множини  для усіх для усіх 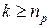 буде виконуватися нерівність буде виконуватися нерівність
 . .
Оскільки число  не залежить від не залежить від 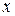 , то на множині , то на множині  послідовність функцій послідовність функцій  збігається рівномірно до функції збігається рівномірно до функції  . .
Теорема доведена.
ГЛАВА Y
Інтеграл Лебега
|



 послідовності вимірних функцій
послідовності вимірних функцій  , що збігається у кожній точки множина
, що збігається у кожній точки множина  ,- вимірна.
,- вимірна.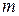 ,
,  і довільного числа
і довільного числа 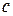 розглянемо вимірну множину
розглянемо вимірну множину  . Теорема буде доведена, якщо одержимо рівність
. Теорема буде доведена, якщо одержимо рівність .
. , тобто
, тобто 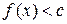 . Знайдемо натуральне число
. Знайдемо натуральне число  таке, що
таке, що  , а потім, використовуючи властивості границі, знайдемо таке натуральне число
, а потім, використовуючи властивості границі, знайдемо таке натуральне число  , починаючи з якого
, починаючи з якого  . Тоді елемент
. Тоді елемент  і отже належить правої частини. Навпаки, якщо елемент
і отже належить правої частини. Навпаки, якщо елемент  , то знайдуться натуральні числа
, то знайдуться натуральні числа  . Переходячи в останній нерівності до границі, коли
. Переходячи в останній нерівності до границі, коли  , дістанемо
, дістанемо
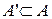 , міра якої дорівнює нулю.
, міра якої дорівнює нулю. , задані і вимірні на множині
, задані і вимірні на множині  .
.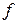 ~
~  .
.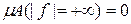 .
.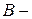 підмножина тих елементів множини
підмножина тих елементів множини  має міру нудь, отже на підставі властивості 1,
має міру нудь, отже на підставі властивості 1,  послідовність скінченних вимірних функцій
послідовність скінченних вимірних функцій 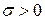 міра множини
міра множини  прямує до нуля, коли
прямує до нуля, коли 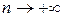 . При цьому у множину
. При цьому у множину  і
і  .
. вимірні,
вимірні,  . Тому, на підставі властивості 12 вимірних множин,
. Тому, на підставі властивості 12 вимірних множин, 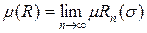 . Покажемо, що
. Покажемо, що  . Нехай елемент
. Нехай елемент 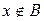 . Тоді в точці
. Тоді в точці 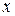 послідовність
послідовність  має місце нерівність
має місце нерівність .
. , і тим паче перетину
, і тим паче перетину  . Оскільки
. Оскільки  , то і
, то і  . Тому
. Тому  , коли
, коли 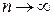 , але першим доданком об’єднання, що визначає
, але першим доданком об’єднання, що визначає  , коли
, коли  розіб’ємо півінтервал
розіб’ємо півінтервал  на
на  і визначимо групу з
і визначимо групу з 
 прості і тому вимірні на півінтервалі
прості і тому вимірні на півінтервалі  так, щоб функції з більшим верхнім індексом (з однієї групи) слідували за функцією з меншим індексом. Цю послідовність позначимо символом
так, щоб функції з більшим верхнім індексом (з однієї групи) слідували за функцією з меншим індексом. Цю послідовність позначимо символом  . Очевидно, що
. Очевидно, що  , де
, де  Послідовність функцій
Послідовність функцій  . Дійсно, для будь-якого
. Дійсно, для будь-якого 
 .
. такий, що
такий, що  . Тоді
. Тоді  , а всі інші функції з цієї групи в точці
, а всі інші функції з цієї групи в точці  , що збігається майже скрізь на множині
, що збігається майже скрізь на множині  прямує до нуля, а послідовність невід’ємних чисел
прямує до нуля, а послідовність невід’ємних чисел 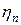 така, що ряд
така, що ряд  збігається. Знайдемо натуральне число
збігається. Знайдемо натуральне число  таке, що
таке, що .
. прямує до нуля, коли
прямує до нуля, коли  таке, що
таке, що  і
і .
. . Знайдемо натуральне число
. Знайдемо натуральне число 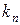 таке, що
таке, що  і
і .
. і
і 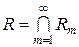 .
. вимірні,
вимірні,  . Тому, на підставі властивості 12 вимірних множин,
. Тому, на підставі властивості 12 вимірних множин,  . Завдяки вибору послідовності чисел
. Завдяки вибору послідовності чисел 
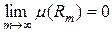 , отже
, отже  послідовність
послідовність  , тоді
, тоді  і отже знайдеться натуральне число
і отже знайдеться натуральне число  , тобто для усіх
, тобто для усіх  елемент
елемент  . Отже
. Отже для усіх
для усіх  існує вимірна множина
існує вимірна множина  така, що
така, що .
. послідовність функцій
послідовність функцій 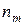 таке, що
таке, що .
.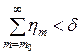 і покладемо
і покладемо  . На підставі наслідку 5 із властивості 8 вимірних множин
. На підставі наслідку 5 із властивості 8 вимірних множин ,
, , що
, що 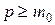 і
і  . Це можливо тому, що
. Це можливо тому, що  , коли
, коли 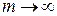 . Нехай
. Нехай  , тоді
, тоді 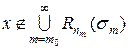 і отже
і отже  . Внаслідок означення множини
. Внаслідок означення множини 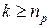 буде виконуватися нерівність
буде виконуватися нерівність .
. не залежить від
не залежить від 


