Канторова відкрита множина, канторова досконала множина
Трійковим дробом називається сума ряду  , де , де  або 1, або 2. Цей ряд збігається, сума його невід’ємна і не перевищує одиниці, тому що члени його мажоруються членами геометричної прогресії. Трійковий дріб будемо зображати символом або 1, або 2. Цей ряд збігається, сума його невід’ємна і не перевищує одиниці, тому що члени його мажоруються членами геометричної прогресії. Трійковий дріб будемо зображати символом  і також називати трійковим дробом. Трійковий дріб виду і також називати трійковим дробом. Трійковий дріб виду 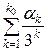 , де , де 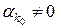 , називається трійково-раціональним числом. Ця сума дорівнює раціональному числу , називається трійково-раціональним числом. Ця сума дорівнює раціональному числу  , де ціле число , де ціле число 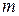 менше за менше за  . Трійково-раціональне число . Трійково-раціональне число 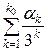 , де , де 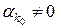 , крім зображення , крім зображення  (запис (0) («0 в періоді») означає, що усі (запис (0) («0 в періоді») означає, що усі  якщо якщо  ) має зображення ) має зображення 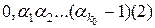 (запис (2) («2 в періоді») означає, що усі (запис (2) («2 в періоді») означає, що усі  якщо якщо  ). Має місце наступне твердження. ). Має місце наступне твердження.
Теорема 2.1.6 Будь-яке число  можливо зобразити трійковим дробом. При цьому зображення єдине, якщо можливо зобразити трійковим дробом. При цьому зображення єдине, якщо 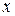 не є трійково-раціональним числом. не є трійково-раціональним числом.
Доведення теореми 2.1.6 аналогічне доведенню теореми 1.4.2.
Далі розглянемо наступні інтервали. Нехай 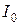 є інтервал (0,1; 0,1(2)) і для кожного k= 1,2,… розглянемо є інтервал (0,1; 0,1(2)) і для кожного k= 1,2,… розглянемо  інтервалів інтервалів  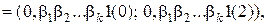 де де 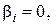 або 2. Довжина кожного з них дорівнює або 2. Довжина кожного з них дорівнює  . Очевидно, що інтервали . Очевидно, що інтервали 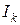 можливо зобразити у вигляду можливо зобразити у вигляду  . .
Лема 2.1.1. Різним наборам чисел  відповідають різні інтервали відповідають різні інтервали 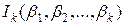 . Крім того вони не перетинаються, не мають спільних кінців і, очевидно, що точки 0 і 1 не є кінцями ціх інтервалів. . Крім того вони не перетинаються, не мають спільних кінців і, очевидно, що точки 0 і 1 не є кінцями ціх інтервалів.
Дійсно, нехай  , де , де 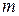 і і  довільні. Покажемо, що лівий кінець інтервала довільні. Покажемо, що лівий кінець інтервала  більше правого більше правого
кінця інтервалу 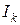 : :

 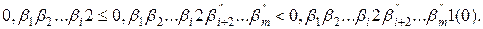
Із означень інтервалів 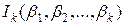 випливає, що точки 0 і 1 не є кінцями ціх інтервалів. випливає, що точки 0 і 1 не є кінцями ціх інтервалів.
Арифметична характеристика чисел, які належать інтервалам 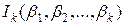 . .
Лема 2.1.2. Для того, щоб  необхідно і достатньо, щоб число необхідно і достатньо, щоб число 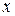 в трійковому запису мало вигляд в трійковому запису мало вигляд  , де , де  або 2, а або 2, а  довільні і хоча б одно з них не дорівнює нулю і хоча б одно з них не дорівнює 2. довільні і хоча б одно з них не дорівнює нулю і хоча б одно з них не дорівнює 2.
Достатність. Нехай число 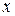 в трійковому запису має вигляд в трійковому запису має вигляд  , де , де  або 2, а або 2, а  довільні і хоча б одно з них не дорівнює нулю і хоча б одно з них не дорівнює 2. Тоді: довільні і хоча б одно з них не дорівнює нулю і хоча б одно з них не дорівнює 2. Тоді:
 . .
Необхідність. Якщо  , то , то 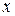 повинно бути більше за лівий кінець інтервалу повинно бути більше за лівий кінець інтервалу 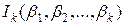 , тобто , тобто  , де хоча б одна з цифр , де хоча б одна з цифр  не дорівнює нулю (тому що у протилежному випадку не дорівнює нулю (тому що у протилежному випадку 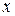 збігається з лівим кінцем інтервалу збігається з лівим кінцем інтервалу 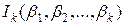 і отже не належить йому), а з іншого боку і отже не належить йому), а з іншого боку 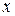 повинно бути менше за правий кінець інтервалу повинно бути менше за правий кінець інтервалу 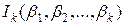 , тобто , тобто  , де хоча б одна з цифр , де хоча б одна з цифр  не дорівнює двом, тому що у протилежному випадку не дорівнює двом, тому що у протилежному випадку 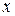 збігається з правим кінцем інтервалу збігається з правим кінцем інтервалу 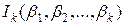 і тому не належить йому. Лему доведено. і тому не належить йому. Лему доведено.
Побудова Канторових множин.
Поступимо наступним чином: вилучимо з сегмента  спочатку інтервал спочатку інтервал 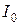 , потім два інтервалу , потім два інтервалу  , на , на  му кроці вилучимо му кроці вилучимо  інтервалів інтервалів 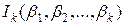 . Об’єднання усіх інтервалів . Об’єднання усіх інтервалів 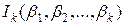 називається Канторовою відкритою множиною і позначається через називається Канторовою відкритою множиною і позначається через 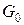 , а доповнення множини , а доповнення множини 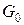 до сегмента до сегмента  називається Канторовою досконалою множиною і позначається через називається Канторовою досконалою множиною і позначається через  . За лемою 2.1.2 Канторова відкрита множина це множина усіх чисел з сегмента . За лемою 2.1.2 Канторова відкрита множина це множина усіх чисел з сегмента  , трійковий запис яких неможливий без цифри 1. Наприклад, число (в трійковому запису) 0,1 має також вигляд 0,0(2), а тому воно не належить множині , трійковий запис яких неможливий без цифри 1. Наприклад, число (в трійковому запису) 0,1 має також вигляд 0,0(2), а тому воно не належить множині 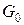 . Канторова досконала множина дійсно досконала тому, що одержується з сегмента . Канторова досконала множина дійсно досконала тому, що одержується з сегмента  вилученням зчисленної множина інтервалів вилученням зчисленної множина інтервалів 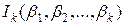 , що не мають спільних кінців і точки 0 і 1 не є кінцями ціх інтервалів. З арифметичної характеристики множини , що не мають спільних кінців і точки 0 і 1 не є кінцями ціх інтервалів. З арифметичної характеристики множини 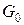 випливає, що Канторова досконала множина це множина усіх чисел сегмента випливає, що Канторова досконала множина це множина усіх чисел сегмента  , трійковий запис яких містить тільки цифри 0 і 2, тобто це множина усіх трійкових дробів вигляду , трійковий запис яких містить тільки цифри 0 і 2, тобто це множина усіх трійкових дробів вигляду  , де , де  або 2, отже це множина потужності континууму. Обчислимо суму довжин вилучених інтервалів: Спочатку вилучається інтервал або 2, отже це множина потужності континууму. Обчислимо суму довжин вилучених інтервалів: Спочатку вилучається інтервал 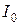 , довжина якого дорівнює , довжина якого дорівнює  , потім два інтервала, довжина кожного з яких дорівнює , потім два інтервала, довжина кожного з яких дорівнює  , на , на  му кроці вилучається му кроці вилучається  інтервалів інтервалів 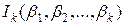 , довжина кожного з яких дорівнює , довжина кожного з яких дорівнює  . Отже, сума довжин вилучених інтервалів дорівнює . Отже, сума довжин вилучених інтервалів дорівнює

Означення 2.1.5 Сім’я  відкритих множин називається покриттям множини відкритих множин називається покриттям множини  , якщо , якщо 
Лема 2.1.3. (Гейне-Бореля). Із будь-якого покриття замкненої обмеженої множини  відкритими множинами можна виділити скінченнне покриття. відкритими множинами можна виділити скінченнне покриття.
Доведення. Припустимо, що лема не має місце. Так як множина  обмежена, то знайдеться сегмент обмежена, то знайдеться сегмент 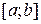 , що містить множину , що містить множину  . Нехай . Нехай  . Тоді хоча б для одної з замкнених множин . Тоді хоча б для одної з замкнених множин  або або  не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через  , а сегмент, в якому вона міститься через , а сегмент, в якому вона міститься через  . Очевидно, що . Очевидно, що  і довжина сегмента і довжина сегмента  у два рази менша довжини сегмент у два рази менша довжини сегмент 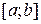 : :  =1/2 =1/2  . Нехай побудована послідовність вкладених сегментів . Нехай побудована послідовність вкладених сегментів  таких, що для множин таких, що для множин  неможливо вилучити скінченнне покриття, неможливо вилучити скінченнне покриття,  , а також , а також  = =  . Нехай . Нехай 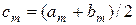 . Тоді хоча б для одної з замкнених множин . Тоді хоча б для одної з замкнених множин  або або  не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через  , а сегмент, в якому вона міститься через , а сегмент, в якому вона міститься через  . .
Внаслідок принципу математичної індукції існують послідовність вкладених сегментів  , довжини яких прямують до нуля, і послідовність вкладених замкнених множин , довжини яких прямують до нуля, і послідовність вкладених замкнених множин  , таких, що для кожної з них неможливо вилучити скінченнне покриття. , таких, що для кожної з них неможливо вилучити скінченнне покриття.
За теоремою про послідовніть вкладених сегментів існує єдина спільна точка  . Тоді точка . Тоді точка 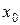 є граничною точкою замкненої множини є граничною точкою замкненої множини  і, отже належить до неї. Нехай і, отже належить до неї. Нехай  - відкрита множина з даного покриття, що містить точку - відкрита множина з даного покриття, що містить точку 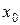 , і , і  . Якщо . Якщо 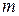 таке, що таке, що  , то усі сегменти , то усі сегменти  за умовою, що за умовою, що  . Отже всі множини . Отже всі множини  покриваються відкритою множиною покриваються відкритою множиною  за умовою, що за умовою, що  , а це суперечить властивостям множин , а це суперечить властивостям множин  . Одержана суперечність спростовує припущення. Лема доведена. . Одержана суперечність спростовує припущення. Лема доведена.
Зауваження. Лема Гейне-Бореля має місце і в просторі  . .
ГЛАВА III
МІРА ЛЕБЕГА ОБМЕЖЕНИХ МНОЖИН У 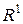
|



 , де
, де  або 1, або 2. Цей ряд збігається, сума його невід’ємна і не перевищує одиниці, тому що члени його мажоруються членами геометричної прогресії. Трійковий дріб будемо зображати символом
або 1, або 2. Цей ряд збігається, сума його невід’ємна і не перевищує одиниці, тому що члени його мажоруються членами геометричної прогресії. Трійковий дріб будемо зображати символом  і також називати трійковим дробом. Трійковий дріб виду
і також називати трійковим дробом. Трійковий дріб виду 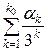 , де
, де 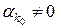 , називається трійково-раціональним числом. Ця сума дорівнює раціональному числу
, називається трійково-раціональним числом. Ця сума дорівнює раціональному числу  , де ціле число
, де ціле число 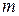 менше за
менше за  . Трійково-раціональне число
. Трійково-раціональне число  (запис (0) («0 в періоді») означає, що усі
(запис (0) («0 в періоді») означає, що усі  якщо
якщо  ) має зображення
) має зображення 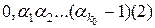 (запис (2) («2 в періоді») означає, що усі
(запис (2) («2 в періоді») означає, що усі  якщо
якщо  можливо зобразити трійковим дробом. При цьому зображення єдине, якщо
можливо зобразити трійковим дробом. При цьому зображення єдине, якщо 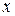 не є трійково-раціональним числом.
не є трійково-раціональним числом.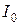 є інтервал (0,1; 0,1(2)) і для кожного k= 1,2,… розглянемо
є інтервал (0,1; 0,1(2)) і для кожного k= 1,2,… розглянемо  інтервалів
інтервалів 
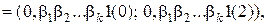 де
де 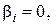 або 2. Довжина кожного з них дорівнює
або 2. Довжина кожного з них дорівнює  . Очевидно, що інтервали
. Очевидно, що інтервали 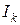 можливо зобразити у вигляду
можливо зобразити у вигляду  .
. відповідають різні інтервали
відповідають різні інтервали 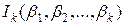 . Крім того вони не перетинаються, не мають спільних кінців і, очевидно, що точки 0 і 1 не є кінцями ціх інтервалів.
. Крім того вони не перетинаються, не мають спільних кінців і, очевидно, що точки 0 і 1 не є кінцями ціх інтервалів. , де
, де  довільні. Покажемо, що лівий кінець інтервала
довільні. Покажемо, що лівий кінець інтервала  більше правого
більше правого

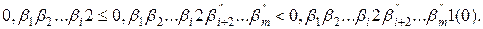
 необхідно і достатньо, щоб число
необхідно і достатньо, щоб число  , де
, де  або 2, а
або 2, а  довільні і хоча б одно з них не дорівнює нулю і хоча б одно з них не дорівнює 2.
довільні і хоча б одно з них не дорівнює нулю і хоча б одно з них не дорівнює 2. .
. не дорівнює нулю (тому що у протилежному випадку
не дорівнює нулю (тому що у протилежному випадку  спочатку інтервал
спочатку інтервал  , на
, на 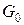 , а доповнення множини
, а доповнення множини  . За лемою 2.1.2 Канторова відкрита множина це множина усіх чисел з сегмента
. За лемою 2.1.2 Канторова відкрита множина це множина усіх чисел з сегмента  , трійковий запис яких неможливий без цифри 1. Наприклад, число (в трійковому запису) 0,1 має також вигляд 0,0(2), а тому воно не належить множині
, трійковий запис яких неможливий без цифри 1. Наприклад, число (в трійковому запису) 0,1 має також вигляд 0,0(2), а тому воно не належить множині  , де
, де  , потім два інтервала, довжина кожного з яких дорівнює
, потім два інтервала, довжина кожного з яких дорівнює  , на
, на 
 відкритих множин називається покриттям множини
відкритих множин називається покриттям множини  , якщо
, якщо 
 відкритими множинами можна виділити скінченнне покриття.
відкритими множинами можна виділити скінченнне покриття. обмежена, то знайдеться сегмент
обмежена, то знайдеться сегмент 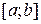 , що містить множину
, що містить множину  . Тоді хоча б для одної з замкнених множин
. Тоді хоча б для одної з замкнених множин  або
або  не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через
не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через  , а сегмент, в якому вона міститься через
, а сегмент, в якому вона міститься через  . Очевидно, що
. Очевидно, що  і довжина сегмента
і довжина сегмента  =1/2
=1/2  . Нехай побудована послідовність вкладених сегментів
. Нехай побудована послідовність вкладених сегментів  таких, що для множин
таких, що для множин  неможливо вилучити скінченнне покриття,
неможливо вилучити скінченнне покриття,  , а також
, а також  =
=  . Нехай
. Нехай 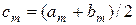 . Тоді хоча б для одної з замкнених множин
. Тоді хоча б для одної з замкнених множин  або
або  не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через
не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через  , а сегмент, в якому вона міститься через
, а сегмент, в якому вона міститься через  .
. , довжини яких прямують до нуля, і послідовність вкладених замкнених множин
, довжини яких прямують до нуля, і послідовність вкладених замкнених множин  , таких, що для кожної з них неможливо вилучити скінченнне покриття.
, таких, що для кожної з них неможливо вилучити скінченнне покриття. . Тоді точка
. Тоді точка 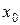 є граничною точкою замкненої множини
є граничною точкою замкненої множини  - відкрита множина з даного покриття, що містить точку
- відкрита множина з даного покриття, що містить точку  . Якщо
. Якщо  , то усі сегменти
, то усі сегменти  за умовою, що
за умовою, що  . Отже всі множини
. Отже всі множини  покриваються відкритою множиною
покриваються відкритою множиною  .
.