
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Граничний перехід під знаком інтеграла ЛебегаСодержание книги
Поиск на нашем сайте
Теорема 5.3.1 (Теорема Лебега). Нехай послідовність вимірних майже скрізь скінченних на множині
Доведення. На підставі теореми Рісса існує підпослідовність
Щоб оцінити перший доданок у правій частини нерівності (5.3.2) застосуємо властивість 6:
Для заданого
якщо
Таким чином із нерівностей (5.3.3) - (5.3.4) для усіх
Теорема доведена. Наслідок 5.3.1 Нехай послідовність вимірних на множині Доведення. З а теоремою Лебега (див. теорему 4.1.4) послідовність функцій Ще більш простий варіант теореми Лебега одержимо, якщо функцію Наслідок 5.3.2 Нехай послідовність вимірних на множині Доведення. Якщо послідовність вимірних на множині
Теорема 5.3.2 (теорема Леві). Нехай
Тоді майже скрізь на множині
Доведення. З монотонності послідовності функцій Введемо множину Нехай
Використовуючи нерівність (5.3.7), наслідок 2 і умову (5.3.5) одержимо
Отже функція Теорема доведена. Наслідок 5.3.3. Твердження теореми Леві збережеться, якщо функції послідовності
Порівнюючи початок і кінець рядка рівностей одержимо (5.3.6). Наслідок 5.3.4. Нехай
збігається. Тоді сума ряду
Доведення. Нехай
Отже виконуються умови теореми Леві, застосовуючи яку одержимо (5.3.8).
Теорема 5.3.3 (теорема Фату). Нехай
Тоді функція
Доведення. Нехай
Отже для послідовності функцій
Покажемо, що якщо послідовність для усіх Покажемо тепер, що якщо
Тобто Теорема доведена.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.10.195 (0.007 с.) |

 функцій
функцій  збігається за мірою до майже скрізь скінченної функції
збігається за мірою до майже скрізь скінченної функції 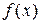 і існує невід’ємна інтегровна за Лебегом функція
і існує невід’ємна інтегровна за Лебегом функція  така, що майже скрізь на множині
така, що майже скрізь на множині  . Тоді функція
. Тоді функція 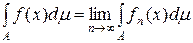 . (5.3.1)
. (5.3.1) , що збігається майже скрізь на множині
, що збігається майже скрізь на множині  майже скрізь на множині
майже скрізь на множині 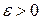 візьмемо таке число
візьмемо таке число 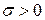 , що
, що  . Нехай
. Нехай  і
і  . Використовуючи адитивність інтеграла, властивість 6 і нерівність
. Використовуючи адитивність інтеграла, властивість 6 і нерівність  , яка виконується майже скрізь, одержимо
, яка виконується майже скрізь, одержимо (5.3.2)
(5.3.2)
 , що
, що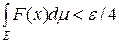 , (5.3.3)
, (5.3.3) . Оскільки послідовність функцій
. Оскільки послідовність функцій  прямує до нуля, тому знайдеться число
прямує до нуля, тому знайдеться число 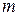 таке, що для усіх
таке, що для усіх  має місце нерівність
має місце нерівність 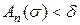 . Отже, для усіх
. Отже, для усіх  . (5.3.4)
. (5.3.4) .
. така, що майже скрізь на множині
така, що майже скрізь на множині  . Тоді функція
. Тоді функція 
 . (5.3.5)
. (5.3.5) , покажемо, що майже скрізь ця границя скінченна.
, покажемо, що майже скрізь ця границя скінченна. і покажемо, що
і покажемо, що  . Для довільного числа
. Для довільного числа 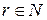 множина
множина  . Дійсно, якщо
. Дійсно, якщо  , то
, то  існує натуральне число
існує натуральне число  . Отже
. Отже  . Завдяки тому, що послідовність
. Завдяки тому, що послідовність 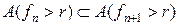 і тоді
і тоді  . Внаслідок нерівності Чебишева і умови теореми
. Внаслідок нерівності Чебишева і умови теореми  . Отже
. Отже 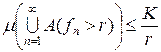 і для будь-якого
і для будь-якого  :
:  . Отже
. Отже  . Множини
. Множини  вимірні, попарно неперетинні і
вимірні, попарно неперетинні і 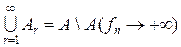 . На множені
. На множені  визначимо просту функцію
визначимо просту функцію  , якщо
, якщо  і покажемо, що вона інтегровна на множені
і покажемо, що вона інтегровна на множені  , тобто доведемо збіжність ряду
, тобто доведемо збіжність ряду  . Позначимо через
. Позначимо через  і оцінимо частину суму
і оцінимо частину суму  . Із означення функції
. Із означення функції  випливає нерівність
випливає нерівність . (5.3.7)
. (5.3.7)
 .
. . Таким чином для послідовності функцій
. Таким чином для послідовності функцій  і константу
і константу 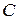 в умові (5.3.5) замінити на
в умові (5.3.5) замінити на  . Тоді функція
. Тоді функція 
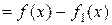 інтегровна на множені
інтегровна на множені  .
. послідовність невід’ємних і інтегровних на множені
послідовність невід’ємних і інтегровних на множені 
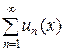 є функція інтегровна на множені
є функція інтегровна на множені  =
= 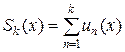 . Оскільки
. Оскільки  послідовність невід’ємних і інтегровних на множені
послідовність невід’ємних і інтегровних на множені  неспадаюча, послідовність невід’ємних і інтегровних на множені
неспадаюча, послідовність невід’ємних і інтегровних на множені  .
. . (5.3.10)
. (5.3.10) Функції
Функції 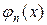 вимірні на множені
вимірні на множені  . Оскільки
. Оскільки  , то
, то  і, за умовою (5.3.9)
і, за умовою (5.3.9) . (5.3.11)
. (5.3.11) інтегровна на множені
інтегровна на множені  .
.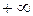 , то послідовність
, то послідовність  довільне додатне число. Існує число
довільне додатне число. Існує число  таке, що для будь-якого
таке, що для будь-якого  виконується нерівність
виконується нерівність  . Тоді
. Тоді . Отже
. Отже  . Так як функція
. Так як функція  майже скрізь скінченна, то і
майже скрізь скінченна, то і  , то
, то 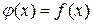 . Нехай
. Нехай  . Тоді, очевидно, що
. Тоді, очевидно, що  і для усіх
і для усіх  . Отже для усіх
. Отже для усіх  ,
,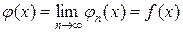 майже скрізь і має місце нерівність (5.3.10).
майже скрізь і має місце нерівність (5.3.10).


