
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття зовнішньої міри обмеженої множини і її властивості.Содержание книги
Поиск на нашем сайте
Означення 3.3.1 Нехай
де точна нижня межа береться по усім скінченним або зчисленним об’єднанням елементарних множин
Властивості зовнішній міри. 1. Зовнішня міра невід’ємна. 2. Зовнішня міра елементарної множини Доведення. Якщо
3. Якщо обмежена множина Ця властивість випливає з означення зовнішньої міри і називається монотонністю. 4. Якщо обмежена множина Доведення. В силу властивості точної нижньої межі для кожної множини
Спрямувавши e до нуля, одержимо указану властивість.
5. Для будь-яких обмежених множин
Доведення. Використовавши співвідношення Поняття вимірної множини Означення 3.4.1 Обмежена множина
Якщо множина
Із означення вимірної множини випливає, що будь-яка елементарна множина Властивості вимірних множин.
1. Якщо множина Доведення випливає з рівності
2. Об’єднання скінченної сім’ї вимірних множин є множина вимірна. Доведення. Розглянемо спочатку дві множини
Так як об’єднання скінченної множини елементарних множин є елементарна множина, то, використовуючи включення
і властивості 3,4 зовнішньої міри, одержимо.
Припустивши вимірність об’єднання
3. Перетин скінченної сім’ї вимірних множин є множина вимірна. Доведення і в цьому випадку достатньо провести для двох множин
За властивостю 1 доданки у правій частині вимірні, і завдяки властивості 2 вимірна права частина, а тоді за властивістю 1 вимірна множина
4. Різниця Доведення. Нехай інтервал 5. Симетрична різниця вимірних множин Ця властивість випливає з останньої властивості, властивості 2 і рівності
6. Адитивність міри. Міра об’єднання скінченної сім’ї вимірних попарно неперетинних множин Доведення. Спочатку розглянемо дві множини
За означенням вимірності, для будь-якого числа
Надалі значок, що позначає зовнішню міру, будемо опускати тому, що усі множини вимірні. Розглянемо наступні співвідношення і нерівності. Оскільки множини
і, тим більше,
А тоді, внаслідок (3.4.2)
З властивості 5 зовнішньої міри (див. нерівність (3.3.2)) випливає, що
і, аналогічно, використовуючи включення
одержимо
Завдяки адитивності міри елементарних множин (див. наслідок 3)
Застосуємо спочатку нерівність (3.4.6), потім рівність (3.4.7) і на кінець нерівності (3.4.3 – 3.4.5)
В силу довільності e одержимо нерівність
що разом з (3.4.1) дає необхідну рівність.
Припустимо тепер, що властивість має місце для
Розглянемо далі
За принципом математичної індукції, адитивність має місце до будь-якої кількості вимірних попарно неперетинних множин Наслідок 1. Якщо
Доведення аналогічно доведенню такої ж властивості міри елементарних множин. Наслідок 2. Якщо
Доведення. Зобразимо об’єднання множин
Множини і наслідку 1, маємо
Рівність (3.4.8) у теорії ймовірностей називається теоремою додавання. Наслідок 3. Якщо
Доведення. В силу властивості точної нижньої межі для кожної з множин
Тоді на підставі наслідку 2
Спрямувавши e до нуля, одержимо (3.4.9).
7. Обмежено об’єднання зчисленної сім’ї вимірних попарно неперетинних множин Доведення. Нехай
Оскільки множина
Тоді з нерівностей (3.4.10 – 3.4.11) і співвідношення
випливає
8. Обмежено об’єднання зчисленної сім’ї вимірних множин Доведення. Нехай Наслідок 4. Якщо виконуються умови властивості 8, то Доведення.
9. Перетин зчисленної сім’ї вимірних множин Доведення. Нехай 10. Міра обмеженого об’єднання зчисленної сім’ї вимірних попарно неперетинних множин Доведення. Нехай
а з іншого
Отже
11. Нехай вимірні множини
Доведення. Внаслідок монотонності послідовності множин, множини
Використовуючи попередню властивість і наслідок з властивості 6, одержимо
12. Нехай вимірні множини
Доведення. Внаслідок монотонності послідовності множин, множини
Внаслідок співвідношень двоїстості одержимо
13. Нехай множини
Доведення. Внаслідок обмеженості і монотонності послідовності множин і монотонності зовнішньої міри
Щоб довести протилежну нерівність, для кожної множини
Завдяки довільності числа e, маємо
Що разом з (3.4.13) дає рівність (3.4.12). Захід, за допомогою якого визначена міра Лебега на множинах, більш загальних за елементарні множина, називається продовженням міри за Лебегом.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.235 (0.007 с.) |

 - довільна обмежена множина з
- довільна обмежена множина з 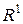 . Число
. Число , (3.3.1)
, (3.3.1) , називається зовнішньою мірою обмеженої множини
, називається зовнішньою мірою обмеженої множини  збігається з
збігається з  , тобто
, тобто  .
. , то в силу властивості 2 міри елементарних множин,
, то в силу властивості 2 міри елементарних множин,  і слід
і слід  . З іншого боку
. З іншого боку  тому, що
тому, що 
 , то
, то  .
.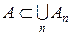 , де
, де 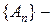 скінченна, або зчисленна сім’я множин, то
скінченна, або зчисленна сім’я множин, то  .
. і довільного числа
і довільного числа 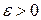 знайдеться скінченна, або зчисленна система елементарних множин
знайдеться скінченна, або зчисленна система елементарних множин  така, що
така, що  і
і  . Тоді
. Тоді  і
і .
. має місце нерівність
має місце нерівність . (3.3.2)
. (3.3.2) і попередню властивість, одержимо
і попередню властивість, одержимо  . Помінявши місцями
. Помінявши місцями  і отже маємо (3.3.2).
і отже маємо (3.3.2). .
. . Міра позначається символом
. Міра позначається символом  і називається мірою Лебега.
і називається мірою Лебега. .
. .
. .
. і
і  . Для будь-якого числа
. Для будь-якого числа  і
і  такі, що
такі, що і
і  .
.
 .
. вимірних множин, в силу рівності
вимірних множин, в силу рівності  одержимо вимірність множини
одержимо вимірність множини  . Завдяки принципу математичної індукції вимірною буде скінченне об’єднання вимірних множин.
. Завдяки принципу математичної індукції вимірною буде скінченне об’єднання вимірних множин. до інтервалу
до інтервалу  . Внаслідок двоїстості операцій об’єднання і перетину
. Внаслідок двоїстості операцій об’єднання і перетину .
.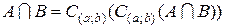
 вимірних множин є множина вимірна.
вимірних множин є множина вимірна. і отже, внаслідок властивостей 1 і 3, різниця – вимірна.
і отже, внаслідок властивостей 1 і 3, різниця – вимірна. .
. , дорівнюю сумі мір, тобто
, дорівнюю сумі мір, тобто  .
. (3.4.1)
(3.4.1)
 .
.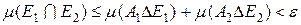 (3.4.3)
(3.4.3) , (3.4.4)
, (3.4.4) , (3.4.5)
, (3.4.5)
 . (3.4.6)
. (3.4.6) . (3.4.7)
. (3.4.7)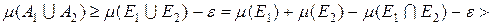
 .
. ,
, вимірних попарно неперетинних множин
вимірних попарно неперетинних множин  тобто
тобто .
. вимірних попарно неперетинних множин
вимірних попарно неперетинних множин  . Тоді, внаслідок властивості для двох множин і припущення одержимо
. Тоді, внаслідок властивості для двох множин і припущення одержимо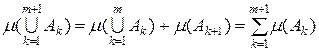 .
. .
. , то
, то .
. . (3.4.8)
. (3.4.8)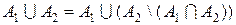
 не перетинаються, тому на підставі властивості 6
не перетинаються, тому на підставі властивості 6 .
.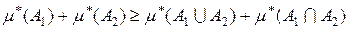 . (3.4.9)
. (3.4.9) така, що
така, що
 і
і  .
.
 .
. є множина вимірна.
є множина вимірна. . Тоді, в силу адитивності міри і обмеженості множини
. Тоді, в силу адитивності міри і обмеженості множини  . Отже ряд
. Отже ряд  збігається. Тоді для довільного числа
збігається. Тоді для довільного числа 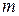 таке, що
таке, що  . Внаслідок властивості 4 зовнішньої міри, одержимо
. Внаслідок властивості 4 зовнішньої міри, одержимо (3.4.10)
(3.4.10) вимірна, то існує елементарна множина
вимірна, то існує елементарна множина  . (3.4.11)
. (3.4.11)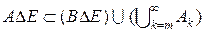
 . Одже множина
. Одже множина  . Множини
. Множини  попарно не перетинаються, вимірні і, як легко перевірити,
попарно не перетинаються, вимірні і, як легко перевірити,  . Отже, внаслідок попередньої властивості,
. Отже, внаслідок попередньої властивості, 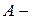 вимірна множина.
вимірна множина.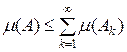 .
. .
. і інтервал
і інтервал  . Тоді
. Тоді  і, внаслідок властивості 6, множина
і, внаслідок властивості 6, множина 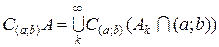 -вимірна, одже множина
-вимірна, одже множина 
 .
.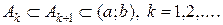 Тоді
Тоді .
. попарно неперетинні і виконується рівність
попарно неперетинні і виконується рівність .
.
 .
. Тоді
Тоді .
. задовольняють умову попередньої властивості. Отже
задовольняють умову попередньої властивості. Отже .
.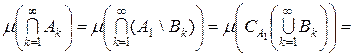
 .
. . (3.4.12)
. (3.4.12) існує і
існує і . (3.4.13)
. (3.4.13) . Нехай
. Нехай 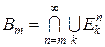 . Очевидно, що
. Очевидно, що 
 і
і  . Використовуючи вимірність множин
. Використовуючи вимірність множин  і властивість 11, одержимо
і властивість 11, одержимо
 .
. ,
,


