Властивості інтеграла Лебега від простих функцій
1. Проста функція  , що задана на множині , що задана на множині  міри нуль, інтегровна за Лебегом і міри нуль, інтегровна за Лебегом і
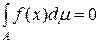 . .
Доведення. Нехай  , якщо , якщо  , де множини , де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і  . Так як . Так як  , то для будь-якого , то для будь-якого  : : 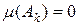 і тоді і тоді
 . .
Отже, функція  інтегровна за Лебегом на множині інтегровна за Лебегом на множині  і і
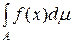 = =  . .
2. Якщо проста функція  обмежена, тобто обмежена, тобто  , то вона інтегровна за Лебегом і , то вона інтегровна за Лебегом і
 . .
Доведення. Обмеженість простої функції  означає, що означає, що  , де , де  значення функції значення функції  . Тоді . Тоді 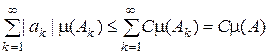 . Отже функція . Отже функція  інтегровна за Лебегом і інтегровна за Лебегом і
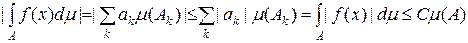 . .
Зауваження 5.1.2. Ця властивість теж підкреслює перевагу інтеграла Лебега в порівнянні з інтегралом Рімана, тому, що, як відомо є обмежені функції (наприклад, функція Діріхле) які не інтегровні за Ріманом.
3. Нехай  , якщо , якщо  , де множини , де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість, попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість,  і і 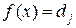 , якщо , якщо  , де множини , де множини 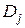 попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість, попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість,  . Тоді . Тоді
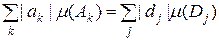 (5.1.1) (5.1.1)
і якщо суми в (5.1.1) скінченні, то
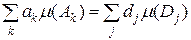 , (5.1.2) , (5.1.2)
тобто існування інтеграла і сам інтеграл не залежить від того, як зображена проста функція.
Доведення. Кожну множину  і кожну множину і кожну множину 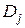 можливо зобразити у вигляді можливо зобразити у вигляді 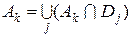 , ,  . Окрім того, . Окрім того,  , якщо , якщо  . Отже . Отже
 . (5.1.3) . (5.1.3)
Суму зліва, використовуючи s-адитивність міри, можливо зобразити у вигляді:
 . .
Аналогічно, суму справа в (5.1.3) зобразимо у вигляді:
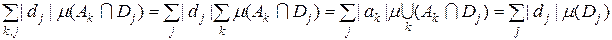 . .
З (5.1.3) і одержаних рівностей випливає (5.1.1). Якщо суми в (5.1.1) скінченні, то з аналогічних міркувань випливає рівність (5.1.2) і
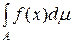 = = 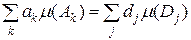 . .
4. Якщо проста функція  інтегровна за Лебегом на множині інтегровна за Лебегом на множині  , то вона інтегровна за Лебегом на будь-якій вимірній підмножині , то вона інтегровна за Лебегом на будь-якій вимірній підмножині 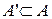 . .
Доведення. Нехай  , якщо , якщо  , де множини , де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і  . Тоді . Тоді  , якщо , якщо 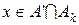 і і 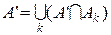 . Так як . Так як  , то , то
 . .
Отже  інтегровна за Лебегом на множині інтегровна за Лебегом на множині 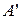 . .
5. Якщо проста функція  інтегровна за Лебегом на множині інтегровна за Лебегом на множині  , то для будь-якого числа lÎ , то для будь-якого числа lÎ 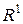 інтегровна за Лебегом функція l інтегровна за Лебегом функція l  і і
 . .
Доведення. Нехай  , якщо , якщо  , де множини , де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і  . Тоді . Тоді  , якщо , якщо  і і
 . .
Отже функція l  інтегровна за Лебегом на множині інтегровна за Лебегом на множині  і і
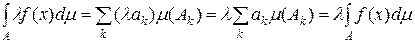 . .
6. Якщо прості функції  і і  інтегровні за Лебегом на множині інтегровні за Лебегом на множині  , то сума , то сума  + +  інтегровна за Лебегом і інтегровна за Лебегом і
 . .
Доведення. Нехай  , якщо , якщо  , де множини , де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість, попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість,  і і  , якщо , якщо  , де множини , де множини 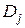 попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість, попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість,  . Тоді . Тоді  + +   , якщо , якщо  , і , і


Отже функція  + +  інтегровна за Лебегом на множині інтегровна за Лебегом на множині  і і

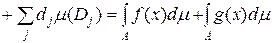 . .
Зауваження 5.1.3. Поняття простої на множині A функції пов’язано з розбиттям множини A на не більш ніж зчисленну суму вимірних множин. З доведення попередньої властивості випливає, що якщо  і і  прості функції задані на множині A, то можливо уважати, що розбиття множини A для функцій прості функції задані на множині A, то можливо уважати, що розбиття множини A для функцій  і і  одне і теж. Цим зауваженням далі будемо користуватись. одне і теж. Цим зауваженням далі будемо користуватись.
7. Якщо для простих інтегровних за Лебегом на множині  функцій функцій  і і  виконується нерівність виконується нерівність  £ £  , то , то
 . .
Доведення. Нехай  , де множини , де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість, і попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість, і  , якщо , якщо  , а , а  , якщо , якщо  . З умови випливає нерівність . З умови випливає нерівність  , і тоді , і тоді
 . .
Ця властивість називається монотонністю інтеграла.
8. Якщо для простих на множині  функцій функцій  і і  виконується нерівність виконується нерівність  £ £  , і функція , і функція  інтегровна за Лебегом на множині інтегровна за Лебегом на множині  , то функція , то функція  інтегровна за Лебегом і інтегровна за Лебегом і
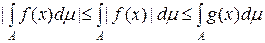 . .
Доведення. Нехай  , де множини , де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість, і попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість, і  , якщо , якщо  , а , а  , якщо , якщо  . З умови випливає нерівність . З умови випливає нерівність  , і , і
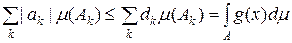 . .
Отже функція  інтегровна за Лебегом і інтегровна за Лебегом і
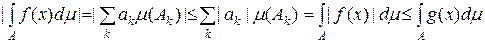 . .
Наслідок 5.1.1. Нехай  є простою функцією на множині є простою функцією на множині  , Для того щоб функція , Для того щоб функція  була інтегровна за Лебегом на множині була інтегровна за Лебегом на множині  , необхідно і досить, щоб була інтегровна функція , необхідно і досить, щоб була інтегровна функція  . .
Дійсно, якщо  інтегровна за Лебегом на множині інтегровна за Лебегом на множині  , то інтегровність функції , то інтегровність функції  випливає з означення інтегровності простої функції. Обернено твердження випливає з попередньої властивості – достатньо взяти випливає з означення інтегровності простої функції. Обернено твердження випливає з попередньої властивості – достатньо взяти  . .
Зауваження 5.1.4. Відомо, що якщо функція  інтегровна за Ріманом, то функція інтегровна за Ріманом, то функція  може не бути інтегровною за Ріманом. Отже наслідок 5.1 показує перевагу інтеграла Лебега в порівнянні з інтегралом Рімана. може не бути інтегровною за Ріманом. Отже наслідок 5.1 показує перевагу інтеграла Лебега в порівнянні з інтегралом Рімана.
9. Якщо для простих на множині  функцій функцій  і і  виконується нерівність виконується нерівність 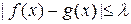 , де , де  деяке дійсне число, і функція деяке дійсне число, і функція  інтегровна за Лебегом на множині інтегровна за Лебегом на множині  , то функція , то функція  інтегровна за Лебегом. інтегровна за Лебегом.
Доведення. З умови випливає нерівність

і отже нерівність
 . .
Використовуючи останню нерівність, наслідок 5.1, приклад 1, властивості 6 і 8 інтеграла одержимо властивість 9.
10. Адитивність інтеграла Лебега. Нехай простафункція  інтегровна за Лебегом на множені інтегровна за Лебегом на множені  і і  деяке розбиття множини деяке розбиття множини  на скінченну або зчисленну множину вимірних множин на скінченну або зчисленну множину вимірних множин 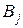 . Тоді . Тоді
 (5.1.4) (5.1.4)
і, якщо справа маємо ряд, то він збігається абсолютно.
Доведення. Нехай  , якщо , якщо  , де множини , де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і  . Тоді, в силу властивості 6, функція . Тоді, в силу властивості 6, функція  інтегровна за Лебегом на кожній множені інтегровна за Лебегом на кожній множені 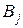 і і
 (5.1.5) (5.1.5)
Так як простафункція  інтегровна за Лебегом на множені інтегровна за Лебегом на множені  , то ряд справа збігається, отже абсолютно збігається ряд , то ряд справа збігається, отже абсолютно збігається ряд  . .
Рівність (5.1.4) випливає з (5.1.5), якщо в (5.1.5) усюди убрати знак модуля.
11. Нехай  деяке розбиття множини деяке розбиття множини  на скінченну або зчисленну множину вимірних множин на скінченну або зчисленну множину вимірних множин 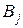 і простафункція і простафункція  інтегровна за Лебегом на кожній множені інтегровна за Лебегом на кожній множені 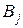 . Якщо збігається ряд . Якщо збігається ряд
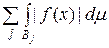 , (5.1.6) , (5.1.6)
то функція  інтегровна за Лебегом на множені інтегровна за Лебегом на множені  . .
Доведення. Нехай  , якщо , якщо  , де множини , де множини  попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і попарно неперетинні, вимірні, їх не більш ніж зчисленна кількість і  . Тоді . Тоді
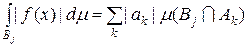
і, оскільки  , то використовуючи збіжність ряду (5.1.6) одержимо , то використовуючи збіжність ряду (5.1.6) одержимо

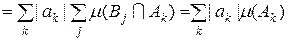 . .
Отже, функція  інтегровна за Лебегом на множені інтегровна за Лебегом на множені  . .
Теорема 5.1.1. (Критерій вимірності функції в термінах простих функцій). Для того щоб скінченна на множені  функція функція  була вимірною необхідно і достатньо, щоб існувала послідовність простих функцій була вимірною необхідно і достатньо, щоб існувала послідовність простих функцій  , що рівномірно збігається на множені , що рівномірно збігається на множені  до функції до функції  . .
Доведення. Достатність випливає з теореми 4.1.2 про граничний перехід у класі вимірних функцій. Доведемо необхідність. Для будь-якого натурального розглянемо множини
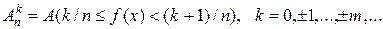
Оскільки функція  вимірна, томножини вимірна, томножини  вимірні і здійснюють розбиття множини вимірні і здійснюють розбиття множини  . Покладемо . Покладемо  , якщо , якщо  . Функції . Функції  прості. Оцінимо різницю прості. Оцінимо різницю  . Нехай . Нехай  , тоді знайдеться ціле число , тоді знайдеться ціле число 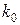 таке, що таке, що 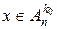 і і
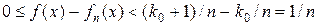 . .
Отже, послідовність простих функцій  рівномірно збігається на множені рівномірно збігається на множені  до функції до функції  . .
Теорема доведена.
|