
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порівняння інтегралів Рімана і ЛебегаСодержание книги
Поиск на нашем сайте
Нехай
і
Отже, функції
де
Окрім того, із нерівностей (5.4.2) випливає, що для функцій
Із (5.4.3) – (5.4.5) одержимо
Теорема 5.4.1 Для того щоб функція
Достатність. Нехай Необхідність. Нехай функція
Теорема 5.4.2 (Теорема Лебега). Для того щоб обмежена функція Достатність. Нехай Необхідність. Нехай функція
із яких випливає нерівність
Візьмемо сегмент
для будь-якого Теорема доведена.
5.5. Інтеграл Лебега по множені нескінченної міри Означення 5.5.1. Нехай Означення 5.5.2. Вимірна функція
яка не залежить від вибору послідовності множин
Покажемо, що границя (5.5.2) існує і скінченна, якщо виконується (5.5.1). Нехай
коли Теорема 5.5.1. Якщо існує невласний інтеграл Рімана від функції Доведення. Розглянемо випадок, коли функція
і
Введемо множини
Із (5.5.3) – (5.5.4) для усіх
З іншого боку, нехай Послідовність функцій
Із нерівностей (5.5.5) – (5.5.6) слідує існування скінченної границі (5.5.1) і рівність Нехай
і тоді Теорема доведена.
Зауваження 5.5.1. Із доведення теореми 5.5.1 випливає, що в означенні 5.5.2, у випадку інтегрованості функції на осі, або проміні, достатньо брати вичерпну послідовність множин
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.01 с.) |

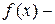 обмежена функція, визначена на сегменті
обмежена функція, визначена на сегменті  , тобто
, тобто , (5.4.1)
, (5.4.1) - послідовність наборів точок сегменту
- послідовність наборів точок сегменту  . Покладемо
. Покладемо 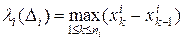 ,
, 
 і визначимо дві послідовності простих функцій:
і визначимо дві послідовності простих функцій: ,
,  . Із означення функцій
. Із означення функцій  ,
,  і (5.4.1) випливає
і (5.4.1) випливає . (5.4.2)
. (5.4.2)
 ,
,  ,
, відповідно нижня і верхня суми Дарбу функції
відповідно нижня і верхня суми Дарбу функції 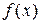 . Оскільки при умові
. Оскільки при умові  виконуються нерівності
виконуються нерівності  , то послідовність функцій
, то послідовність функцій  і
і 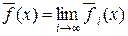 , функції
, функції  і
і  інтегровні за Лебегом на сегменті
інтегровні за Лебегом на сегменті  , (5.4.3)
, (5.4.3) . (5.4.4)
. (5.4.4) . (5.4.5)
. (5.4.5) . (5.4.6)
. (5.4.6) майже скрізь на сегменті
майже скрізь на сегменті  такої, що
такої, що  , коли
, коли  і в цьому випадку функція
і в цьому випадку функція  .
. . Отже функція
. Отже функція 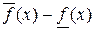 майже скрізь дорівнює нулю. А тоді із нерівностей (5.4.5) випливає еквівалентність функції
майже скрізь дорівнює нулю. А тоді із нерівностей (5.4.5) випливає еквівалентність функції  . Отже, функція
. Отже, функція 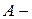 множина точок розриву. Візьмемо будь-яку послідовність
множина точок розриву. Візьмемо будь-яку послідовність  . Множина
. Множина  зчисленна, тому
зчисленна, тому 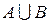 має міру нуль. Покажемо, що у кожній точці
має міру нуль. Покажемо, що у кожній точці  має місце рівність
має місце рівність 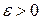 . Внаслідок неперервності функції
. Внаслідок неперервності функції  таке, що
таке, що  , якщо
, якщо 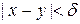 . Оскільки
. Оскільки 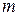 таке, що для усіх
таке, що для усіх  сегменти
сегменти  , що містять точку
, що містять точку 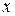 , будуть міститься в інтервалі
, будуть міститься в інтервалі  . Тоді, для усіх
. Тоді, для усіх  , тобто
, тобто  майже скрізь. Позначимо через
майже скрізь. Позначимо через  множину точок сегмента
множину точок сегмента  . Візьмемо будь-яку послідовність
. Візьмемо будь-яку послідовність  має міру нуль. Покажемо, що у кожній точці
має міру нуль. Покажемо, що у кожній точці  функція
функція  ,
, (5.4.7)
(5.4.7) і нерівності (5.4.7) маємо
і нерівності (5.4.7) маємо
 .
.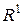 , або проміні
, або проміні  . Послідовність
. Послідовність  вимірних обмежених множин називається вичерпною, якщо вона монотонно зростає, тобто
вимірних обмежених множин називається вичерпною, якщо вона монотонно зростає, тобто  , і
, і  .
. нескінченної міри, називається інтегровною за Лебегом на множині
нескінченної міри, називається інтегровною за Лебегом на множині  , (5.5.1)
, (5.5.1) (5.5.2)
(5.5.2)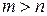 , тоді
, тоді
 ,
, .
. , що задана на осі, або проміні, то існує інтеграл Лебега і вони збігаються.
, що задана на осі, або проміні, то існує інтеграл Лебега і вони збігаються.
 довільна вичерпна послідовність множин. Для довільного числа
довільна вичерпна послідовність множин. Для довільного числа  таке, що
таке, що . (5.5.3)
. (5.5.3) . Послідовність множин
. Послідовність множин  не спадає і
не спадає і  . На підставі властивості 11 вимірних множин
. На підставі властивості 11 вимірних множин  . Тоді знайдеться натуральне число
. Тоді знайдеться натуральне число  виконується нерівність
виконується нерівність  , де число
, де число  , міра якої
, міра якої  , має місце нерівність
, має місце нерівність . (5.5.4)
. (5.5.4) . (5.5.5)
. (5.5.5)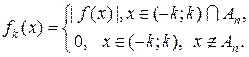
 монотонна, збігається у кожній точці
монотонна, збігається у кожній точці  до функції
до функції 
 (5.5.6)
(5.5.6) .
.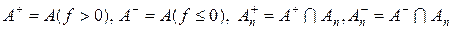 , де
, де 
 .
. .
.


