Теорія міри та інтеграла Лебега
ТЕОРІЯ МІРИ ТА ІНТЕГРАЛА ЛЕБЕГА
ГЛАВА I 
ОСНОВИ ТЕОРІЇ МНОЖИН
Поняття множини, операції над множинами
Означення 1.1.1. Множиною називається сукупність, набір, сім’я, збори, колекція предметів, вибраних по деякому правилу (закону), або просто указаних; при цьому усі предмети різні. Предмети, із яких складається множина називаються елементами.
Множини будемо позначати прописними латинськими буквами, а елементи – малими літерами. Якщо елемент a належить множині A, то це будимо записувати так: а Î А.
Приклади.
1.  множина усіх натуральних чисел, множина усіх натуральних чисел,  множина всіх цілих чисел, множина всіх цілих чисел, 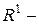 множина всіх дійсних чисел, множина всіх дійсних чисел, 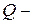 множина всіх раціональних чисел. множина всіх раціональних чисел.
2. Сегмент  множина всіх дійсних чисел множина всіх дійсних чисел 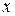 , що задовольняють умову , що задовольняють умову  , інтервал , інтервал  множина всіх дійсних чисел множина всіх дійсних чисел 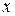 , що задовольняють умову , що задовольняють умову  , півінтервал , півінтервал 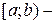 множина всіх дійсних чисел множина всіх дійсних чисел 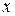 , що задовольняють умову , що задовольняють умову  , півінтервал , півінтервал  множина всіх дійсних чисел множина всіх дійсних чисел 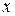 , що задовольняють умову , що задовольняють умову  . .
3.  множина усіх функцій заданих і неперервних на сегменті множина усіх функцій заданих і неперервних на сегменті 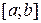 , ,  множина всіх функцій заданих і обмежених на сегменті множина всіх функцій заданих і обмежених на сегменті 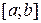 . .
Якщо кожен елемент множини А є елементом множини В, то будемо казати, що множина А міститься в множині В, або множина В містить множину А і позначати це будемо так: А Ì В, або В É А. Будемо також казати, що множина А є підмножиною множини В. Наприклад,  , ,  . .
Якщо кожен елемент множини А є елементом множини В і навпаки кожен елемент множини В є елементом множини А, то множини рівні: А = В. Отже, щоб довести, що множини А і В рівні треба показати, що А Ì В і В Ì А.
Означення 1.1.2. Нехай задана деяка сім’я множин:  . Множина всіх елементів, що належать хоч би однієї із множин даної сім’ї, називається об’єднанням множин . Множина всіх елементів, що належать хоч би однієї із множин даної сім’ї, називається об’єднанням множин  і позначається об’єднання так і позначається об’єднання так 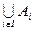 . .
Якщо маємо дві множини А і В, то їх об’єднання позначимо через  . Якщо множин n штук: . Якщо множин n штук:  , то позначення їх об’єднання буде , то позначення їх об’єднання буде  , або , або  . .
Означення 1.1.3. Перетином множин сім’я  називається множина всіх спільних елементів множин даної сім’ї. називається множина всіх спільних елементів множин даної сім’ї.
Позначення перетину: перетин сім’ї множин -  , перетин двох множин - , перетин двох множин - 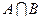 , перетин n множин - , перетин n множин -  , або , або 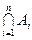 . Якщо множини не мають спільних елементів, то будемо казати, що їх перетин – порожня множина. Порожню множину будемо позначати символом Æ. Порожня множина може бути не тільки результатом перетину. Наприклад: множина дійсних розв’язків рівняння . Якщо множини не мають спільних елементів, то будемо казати, що їх перетин – порожня множина. Порожню множину будемо позначати символом Æ. Порожня множина може бути не тільки результатом перетину. Наприклад: множина дійсних розв’язків рівняння  – порожня множина. – порожня множина.
Означення 1.1.4. Різницею множини А і В називається множина усіх елементів множини А, що не належать множині В. Різниця множин А і В позначається таким чином: А \ В. 
Означення 1.1.5. Симетричною різницею множини А і В називається множина  . Різниця позначається так: . Різниця позначається так:  . .
Означення 1.1.6. Якщо множина В є підмножиною множини А, то різниця множин А і В називається доповнення множини В до множини А. Доповнення множини В до множини А позначається символом  . .
Властивості об’єднання, перетину і доповнення множин (властивості двоїстості).
Теорема 1.1.1 (Співвідношення двоїстості). Нехай кожна із множини  міститься в множині А. Тоді мають місце рівності: міститься в множині А. Тоді мають місце рівності:

Доведення. Нехай  тобто тобто  і і  , отже , отже  для кожного для кожного  і і  . Навпаки, нехай . Навпаки, нехай  , тоді , тоді  і і  для кожного для кожного  . Отже . Отже  і і  . Друга рівність доводиться аналогічно. . Друга рівність доводиться аналогічно.
Задачі.
1. Довести, що  . .
2. Довести, що  . .
3. Довести, що  . .
4. Довести, що  . .
5. Довести, що  тоді і тільки тоді, коли тоді і тільки тоді, коли  . .
6. Довести, що  . .
7. Довести, що  . .
8. Довести, що
9. Довести, що  . .
10. Довести, що  , якщо , якщо  і множини і множини  не перетинаються. не перетинаються.
11. Довести, що  . .
12. Довести, що  . .
13. Верхня границя  послідовності послідовності  є множина є множина  . Довести, що . Довести, що  складається із елементів, що належать нескінченної системи множин складається із елементів, що належать нескінченної системи множин  . .
14. Нижня границя  послідовності послідовності  є множина є множина  . Довести, що . Довести, що  складається із елементів, що належать усім множинам складається із елементів, що належать усім множинам  за виключенням скінченної кількості. за виключенням скінченної кількості.
1.2. Поняття відображення і взаємно однозначначної відповідності
Означення 1.2.1. Правило або закон, по якому кожному елементу а множини А ставиться у відповідність один елемент b множини В, називається функцією обо відображенням множини А в В.
Функція звичайно позначається літерою латинського або грецького алфавіту, наприклад,  і писати і писати  : :  , або , або  , при цьому елемент , при цьому елемент  називається образом елементу називається образом елементу  , а елемент , а елемент  прообразом елемент прообразом елемент  . Множина . Множина  називається образом множини називається образом множини  і позначається символом і позначається символом  . Якщо при перетворенні . Якщо при перетворенні  кожен елемент кожен елемент  є образом деякого елементу є образом деякого елементу  то кажуть, що то кажуть, що  перетворює А на В і це позначають так перетворює А на В і це позначають так  , або , або 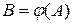 . Множина . Множина  називається прообразом множини називається прообразом множини  і позначається символом і позначається символом 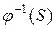 . .
Поряд з термінами «функція» і «відображення» будемо використовувати рівнозначні ім у деяких сітуаціях терміни «перетворення», «оператор», «відповідність».
Означення 1.2.2. Взаємно однозначною відповідністю множин А і В називається відображення  множини А на В, яке різним елементам множини А ставить у відповідність різні елементи множини В. множини А на В, яке різним елементам множини А ставить у відповідність різні елементи множини В.
В цьому випадку прообраз  кожної одно елементної множини кожної одно елементної множини 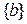 є відображення множини В на А, яке теж є взаємно однозначною відповідністю. Відображення є відображення множини В на А, яке теж є взаємно однозначною відповідністю. Відображення  і і  називаються взаємно оберненими. називаються взаємно оберненими.
Задачі.
1. Нехай  , ,  і і  . Доведіть наступні співвідношення: . Доведіть наступні співвідношення:
 , ,
 , ,
 . .
2. Нехай  , ,  і і  . Доведіть наступні співвідношення: . Доведіть наступні співвідношення:
 , ,
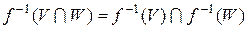 , ,
 . .
Означення 1.2.3. Якщо для множин А і В можливо указати взаємно однозначну відповідність, то множини А і В називається еквівалентними. Еквівалентність множин А і В позначається символом: А ~ В.
Властивості еквівалентних множин:
1. А ~ А.
2. Якщо А ~ В, то В ~ А.
Ця властивість називається транзитивністю.
3. Якщо множини  попарно не перетинаються, множини попарно не перетинаються, множини 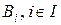 теж попарно не перетинаються і для будь якого теж попарно не перетинаються і для будь якого  ~ ~  , то , то
 ~ ~  . .
4. Нехай А ~ В,  - деяке перетворення - деяке перетворення  , що здійснює взаємно однозначну відповідність, то , що здійснює взаємно однозначну відповідність, то 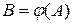 . Якщо . Якщо  -довільна підмножина множини А, то -довільна підмножина множини А, то  . .
5. Якщо А ~ В,  -довільні підмножини множини А, такі що -довільні підмножини множини А, такі що 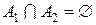 , ,  - деяке перетворення - деяке перетворення  , що здійснює взаємно однозначну відповідність, то , що здійснює взаємно однозначну відповідність, то  і і 
З останньої рівності випливає що   , якщо , якщо  , тобто , тобто  ~ ~  . Дійсно, . Дійсно,  і і  Отже Отже   . .
6. Теорема 1.2.1 (Теорема Кантора-Бернштейна). Нехай підмножина  множини множини  еквівалентна множині еквівалентна множині  , а підмножина , а підмножина  множини множини  еквівалентна множині еквівалентна множині   . Тоді . Тоді  . .
Перед доведенням теореми Кантора-Бернштейна розглянемо лему, яка цікава сама по собі.
Лема 1. 2.1. Якщо  і і  . Тоді . Тоді  . .
Доведення. Нехай  взаємно однозначне перетворення множини взаємно однозначне перетворення множини 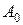 на на  . Покладемо . Покладемо  . З умови леми і означення множин . З умови леми і означення множин  випливає їх монотонність: випливає їх монотонність:  . Дійсно, для . Дійсно, для  , ,  це умова леми. Припустимо, що це умова леми. Припустимо, що  , якщо , якщо 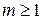 . Тоді . Тоді  , тобто , тобто  . .
Далі, внаслідок властивості 5 еквівалентних множин,
 
і в загальному випадку:

Нехай  . Оскільки . Оскільки  , то , то
 (1.1.1) (1.1.1)
і
 . (1.1.2) . (1.1.2)
Тепер зауважимо, що  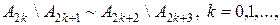 і доданки у правих частинах рівностей (1.1.1) - (1.1.2) попарно не перетинаються. Окрім того і доданки у правих частинах рівностей (1.1.1) - (1.1.2) попарно не перетинаються. Окрім того  . Отже, внаслідок властивості 3 еквівалентних множин, . Отже, внаслідок властивості 3 еквівалентних множин,  . .
Двійкові дроби.
Означення 1.4.2. Двійковим дробом називається сума ряду  , де , де 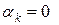 або 1. або 1.
Цей ряд збігається, сума його невід’ємна і не перевищує одиниці тому, що члени його мажоруються членами геометричної прогресії. Отже кожному двійковому дробу відповідає число – сума ряду  . Двійковий дріб будемо зображати символом . Двійковий дріб будемо зображати символом  і також називати двійковим дробом. Двійковий дріб виду і також називати двійковим дробом. Двійковий дріб виду  , де , де 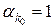 , називається двійково-раціональним числом. Ця сума дорівнює раціональному числу , називається двійково-раціональним числом. Ця сума дорівнює раціональному числу  , де m непарне число менше за , де m непарне число менше за 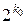 . Двійково-раціональне число . Двійково-раціональне число  крім зображення крім зображення  (запис (0) («0 в періоді») означає, що усі (запис (0) («0 в періоді») означає, що усі  якщо якщо  ) має зображення ) має зображення  . .
Теорема 1.4.2. Кожному числу 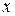 з інтервала (0; 1), що не є двійково-раціональним числом, відповідає єдиний двійковий дріб. з інтервала (0; 1), що не є двійково-раціональним числом, відповідає єдиний двійковий дріб.
Доведення. Нехай  і не є двійково-раціональним числом. Необхідно побудувати і не є двійково-раціональним числом. Необхідно побудувати  для будь-якого для будь-якого  і довести, що частинна сума і довести, що частинна сума 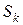 ряду ряду  прямує до числа прямує до числа 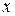 . Визначимо спочатку число . Визначимо спочатку число 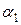 . Якщо . Якщо  , покладемо , покладемо  . Тоді . Тоді  і і  . Якщо . Якщо  , то покладемо , то покладемо  . Тоді . Тоді  і і  . Припустимо, що визначені числа . Припустимо, що визначені числа  , , 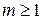 такі, що такі, що  . Знову розглянемо два випадки. Якщо . Знову розглянемо два випадки. Якщо  , то покладемо , то покладемо  . . 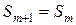 і і  . Якщо . Якщо  , то покладемо , то покладемо  . Тоді . Тоді 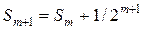 і і  . Число . Число 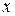 не може дорівнювати не може дорівнювати  , тому що , тому що 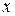 не є двійково-раціональним числом. Слід, в силу принципу математичної індукції, не є двійково-раціональним числом. Слід, в силу принципу математичної індукції,  визначено для будь-якого натурального визначено для будь-якого натурального  і і 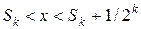 . З останній нерівності випливає . З останній нерівності випливає  . .
Теорема доведена.
Означення 1.4.3. Нехай  множина всіх двійкових дробів, множина всіх двійкових дробів,  множина усіх двійкових дробів, зображення яких містить нескінченну множину чисел множина усіх двійкових дробів, зображення яких містить нескінченну множину чисел  , що дорівнюють 0, , що дорівнюють 0,  множина всіх двійкових дробів, зображення яких містить одиницю в періоді. множина всіх двійкових дробів, зображення яких містить одиницю в періоді.
В силу теореми 1.4.2  має потужність континуум, а множина має потужність континуум, а множина  зчисленна, тому що вона нескінченна і є підмножиною множини раціональних чисел. Отже зчисленна, тому що вона нескінченна і є підмножиною множини раціональних чисел. Отже  - множина потужності континууму. - множина потужності континууму.
Задачі.
1. Довести, що множина  всіх підмножин множини натуральних чисел є множиною потужності континууму. всіх підмножин множини натуральних чисел є множиною потужності континууму.
2. Довести, що множина  всіх підмножин будь-якої зчисленної множини всіх підмножин будь-якої зчисленної множини  є множиною потужності континууму. є множиною потужності континууму.
3. Довести, що множина всіх дійсних функцій, заданих на сегменті  , має потужність більшу, ніж континуум. , має потужність більшу, ніж континуум.
ГЛАВА II
ВІДКРИТІ І ЗАМКНЕНІ МНОЖИНИ В 
Означення 2.1.1 Точка  називається граничною точкою множини називається граничною точкою множини  , якщо у будь-якому околу точки , якщо у будь-якому околу точки  знайдеться хоча б одна точка множина знайдеться хоча б одна точка множина  , що відрізняється від точки , що відрізняється від точки  . .
Теорема 2.1.1. Для того щоб точка  була граничною точкою множини була граничною точкою множини  , необхідно і достатньо щоб у будь-якому околу точки , необхідно і достатньо щоб у будь-якому околу точки  знаходилась нескінченна множина точок з знаходилась нескінченна множина точок з  . .
Доведення. Достатність очевидна, необхідність доведемо від противного. Нехай точка  є граничною точкою множини є граничною точкою множини  , і в деякому околу точки , і в деякому околу точки  знаходиться скінченна множина знаходиться скінченна множина  точок з точок з  , що відрізняється від точки , що відрізняється від точки  . Нехай . Нехай  відстань від точки відстань від точки 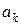 до до  і і  . Тоді в околу радіуса e ні буде не одної точка множини . Тоді в околу радіуса e ні буде не одної точка множини  , що відрізняється від точки , що відрізняється від точки  , а це суперечить тому, що точка , а це суперечить тому, що точка  гранична. Одержана суперечність спростовує припущення. гранична. Одержана суперечність спростовує припущення.
Теорема 2.1.2. Для того щоб точка  була граничною точкою множини була граничною точкою множини  , необхідно і достатньо щоб знайшлась послідовність різних точок з множини , необхідно і достатньо щоб знайшлась послідовність різних точок з множини  , що збігається до точки , що збігається до точки  . .
Доведення. Достатність очевидна, доведемо необхідність. Нехай точка  є граничною точкою множини є граничною точкою множини  і і  послідовність околів радіусу послідовність околів радіусу  . Виберемо довільну точку . Виберемо довільну точку  в околу в околу 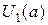 , ,  в околу в околу  , і так далі виберемо точку , і так далі виберемо точку  , яка відрізняється від попередніх и точки , яка відрізняється від попередніх и точки  , і так далі. Оскільки , і так далі. Оскільки  , то послідовність точок , то послідовність точок 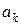 прямує до прямує до  . .
Зауваження. Гранична точка множини  може належати або не належати множині може належати або не належати множині  . Наприклад, граничними точками півінтервала . Наприклад, граничними точками півінтервала  є точки сегмента є точки сегмента 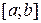 . .
Означення 2.1.2 Множина називається замкненою, якщо вона містить усі свої граничні точки. Далі замкнену множину будемо позначати буквою  . .
Приклади замкнених множин: сегмент  , будь-яка скінченна множина, множина усіх натуральних чисел , будь-яка скінченна множина, множина усіх натуральних чисел  , множина усіх цілих чисел , множина усіх цілих чисел  . .
Означення 2.1.3 Точка  називається внутрішньою точкою множини називається внутрішньою точкою множини  , якщо вона належить , якщо вона належить  разом з деяким околом. разом з деяким околом.
Означення 2.1.4 Множина  називається відкритою, якщо кожна точка множини називається відкритою, якщо кожна точка множини  внутрішня. внутрішня.
Приклади відкритих множин: інтервал  , об'єднання інтервалів. , об'єднання інтервалів.
Означення 2.1.5 Точка  називається ізольованою точкою, якщо існує окіл точки називається ізольованою точкою, якщо існує окіл точки  , який не містить точок множина , який не містить точок множина  , крім точки , крім точки  . .
Означення 2.1.6 Замкнена множина  називається досконалою, якщо кожна точка множини називається досконалою, якщо кожна точка множини  є граничною точкою цієї множини, тобто у множини є граничною точкою цієї множини, тобто у множини  немає ізольованих точок. немає ізольованих точок.
Побудова Канторових множин.
Поступимо наступним чином: вилучимо з сегмента  спочатку інтервал спочатку інтервал 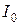 , потім два інтервалу , потім два інтервалу  , на , на  му кроці вилучимо му кроці вилучимо  інтервалів інтервалів 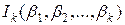 . Об’єднання усіх інтервалів . Об’єднання усіх інтервалів 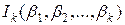 називається Канторовою відкритою множиною і позначається через називається Канторовою відкритою множиною і позначається через 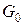 , а доповнення множини , а доповнення множини 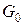 до сегмента до сегмента  називається Канторовою досконалою множиною і позначається через називається Канторовою досконалою множиною і позначається через  . За лемою 2.1.2 Канторова відкрита множина це множина усіх чисел з сегмента . За лемою 2.1.2 Канторова відкрита множина це множина усіх чисел з сегмента  , трійковий запис яких неможливий без цифри 1. Наприклад, число (в трійковому запису) 0,1 має також вигляд 0,0(2), а тому воно не належить множині , трійковий запис яких неможливий без цифри 1. Наприклад, число (в трійковому запису) 0,1 має також вигляд 0,0(2), а тому воно не належить множині 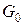 . Канторова досконала множина дійсно досконала тому, що одержується з сегмента . Канторова досконала множина дійсно досконала тому, що одержується з сегмента  вилученням зчисленної множина інтервалів вилученням зчисленної множина інтервалів 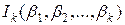 , що не мають спільних кінців і точки 0 і 1 не є кінцями ціх інтервалів. З арифметичної характеристики множини , що не мають спільних кінців і точки 0 і 1 не є кінцями ціх інтервалів. З арифметичної характеристики множини 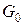 випливає, що Канторова досконала множина це множина усіх чисел сегмента випливає, що Канторова досконала множина це множина усіх чисел сегмента  , трійковий запис яких містить тільки цифри 0 і 2, тобто це множина усіх трійкових дробів вигляду , трійковий запис яких містить тільки цифри 0 і 2, тобто це множина усіх трійкових дробів вигляду  , де , де  або 2, отже це множина потужності континууму. Обчислимо суму довжин вилучених інтервалів: Спочатку вилучається інтервал або 2, отже це множина потужності континууму. Обчислимо суму довжин вилучених інтервалів: Спочатку вилучається інтервал 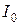 , довжина якого дорівнює , довжина якого дорівнює  , потім два інтервала, довжина кожного з яких дорівнює , потім два інтервала, довжина кожного з яких дорівнює  , на , на  му кроці вилучається му кроці вилучається  інтервалів інтервалів 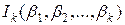 , довжина кожного з яких дорівнює , довжина кожного з яких дорівнює  . Отже, сума довжин вилучених інтервалів дорівнює . Отже, сума довжин вилучених інтервалів дорівнює

Означення 2.1.5 Сім’я  відкритих множин називається покриттям множини відкритих множин називається покриттям множини  , якщо , якщо 
Лема 2.1.3. (Гейне-Бореля). Із будь-якого покриття замкненої обмеженої множини  відкритими множинами можна виділити скінченнне покриття. відкритими множинами можна виділити скінченнне покриття.
Доведення. Припустимо, що лема не має місце. Так як множина  обмежена, то знайдеться сегмент обмежена, то знайдеться сегмент 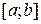 , що містить множину , що містить множину  . Нехай . Нехай  . Тоді хоча б для одної з замкнених множин . Тоді хоча б для одної з замкнених множин  або або  не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через  , а сегмент, в якому вона міститься через , а сегмент, в якому вона міститься через  . Очевидно, що . Очевидно, що  і довжина сегмента і довжина сегмента  у два рази менша довжини сегмент у два рази менша довжини сегмент 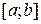 : :  =1/2 =1/2  . Нехай побудована послідовність вкладених сегментів . Нехай побудована послідовність вкладених сегментів  таких, що для множин таких, що для множин  неможливо вилучити скінченнне покриття, неможливо вилучити скінченнне покриття,  , а також , а також  = =  . Нехай . Нехай 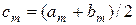 . Тоді хоча б для одної з замкнених множин . Тоді хоча б для одної з замкнених множин  або або  не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через  , а сегмент, в якому вона міститься через , а сегмент, в якому вона міститься через  . .
Внаслідок принципу математичної індукції існують послідовність вкладених сегментів  , довжини яких прямують до нуля, і послідовність вкладених замкнених множин , довжини яких прямують до нуля, і послідовність вкладених замкнених множин  , таких, що для кожної з них неможливо вилучити скінченнне покриття. , таких, що для кожної з них неможливо вилучити скінченнне покриття.
За теоремою про послідовніть вкладених сегментів існує єдина спільна точка  . Тоді точка . Тоді точка 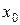 є граничною точкою замкненої множини є граничною точкою замкненої множини  і, отже належить до неї. Нехай і, отже належить до неї. Нехай  - відкрита множина з даного покриття, що містить точку - відкрита множина з даного покриття, що містить точку 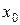 , і , і  . Якщо . Якщо 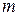 таке, що таке, що  , то усі сегменти , то усі сегменти  за умовою, що за умовою, що  . Отже всі множини . Отже всі множини  покриваються відкритою множиною покриваються відкритою множиною  за умовою, що за умовою, що  , а це суперечить властивостям множин , а це суперечить властивостям множин  . Одержана суперечність спростовує припущення. Лема доведена. . Одержана суперечність спростовує припущення. Лема доведена.
Зауваження. Лема Гейне-Бореля має місце і в просторі  . .
ГЛАВА III
МІРА ЛЕБЕГА ОБМЕЖЕНИХ МНОЖИН У 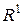
Властивості зовнішній міри.
1. Зовнішня міра невід’ємна.
2. Зовнішня міра елементарної множини  збігається з збігається з  , тобто , тобто  . .
Доведення. Якщо  , то в силу властивості 2 міри елементарних множин, , то в силу властивості 2 міри елементарних множин,  і слід і слід  . З іншого боку . З іншого боку  тому, що тому, що  входить в множину по якої обчислюється точна нижня межа. входить в множину по якої обчислюється точна нижня межа.
3. Якщо обмежена множина   , то , то  . .
Ця властивість випливає з означення зовнішньої міри і називається монотонністю.
4. Якщо обмежена множина  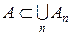 , де , де 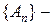 скінченна, або зчисленна сім’я множин, то скінченна, або зчисленна сім’я множин, то  . .
Доведення. В силу властивості точної нижньої межі для кожної множини  і довільного числа і довільного числа 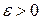 знайдеться скінченна, або зчисленна система елементарних множин знайдеться скінченна, або зчисленна система елементарних множин  така, що така, що  і і  . Тоді . Тоді  і і
 . .
Спрямувавши e до нуля, одержимо указану властивість.
5. Для будь-яких обмежених множин  і і  має місце нерівність має місце нерівність
 . (3.3.2) . (3.3.2)
Доведення. Використовавши співвідношення  і попередню властивість, одержимо і попередню властивість, одержимо  . Помінявши місцями . Помінявши місцями  і і  одержимо одержимо  і отже маємо (3.3.2). і отже маємо (3.3.2).
Поняття вимірної множини
Означення 3.4.1 Обмежена множина  називається вимірною, якщо для довільного числа називається вимірною, якщо для довільного числа 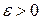 знайдеться елементарна множина знайдеться елементарна множина  така, що така, що
 . .
Якщо множина  вимірна, то її мірою називається вимірна, то її мірою називається  . Міра позначається символом . Міра позначається символом  і називається мірою Лебега. і називається мірою Лебега.
Із означення вимірної множини випливає, що будь-яка елементарна множина  вимірна і у сенсі останнього означення і вимірна і у сенсі останнього означення і  . .
Властивості вимірних множин.
1. Якщо множина  вимірна, то вимірне доповнення множина до відрізка вимірна, то вимірне доповнення множина до відрізка  . .
Доведення випливає з рівності
 . .
2. Об’єднання скінченної сім’ї вимірних множин є множина вимірна.
|




 множина усіх натуральних чисел,
множина усіх натуральних чисел,  множина всіх цілих чисел,
множина всіх цілих чисел, 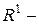 множина всіх дійсних чисел,
множина всіх дійсних чисел, 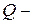 множина всіх раціональних чисел.
множина всіх раціональних чисел. множина всіх дійсних чисел
множина всіх дійсних чисел 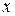 , що задовольняють умову
, що задовольняють умову  , інтервал
, інтервал  множина всіх дійсних чисел
множина всіх дійсних чисел  , півінтервал
, півінтервал 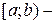 множина всіх дійсних чисел
множина всіх дійсних чисел  , півінтервал
, півінтервал  множина всіх дійсних чисел
множина всіх дійсних чисел  .
. множина усіх функцій заданих і неперервних на сегменті
множина усіх функцій заданих і неперервних на сегменті 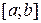 ,
,  множина всіх функцій заданих і обмежених на сегменті
множина всіх функцій заданих і обмежених на сегменті  ,
,  .
. . Множина всіх елементів, що належать хоч би однієї із множин даної сім’ї, називається об’єднанням множин
. Множина всіх елементів, що належать хоч би однієї із множин даної сім’ї, називається об’єднанням множин  і позначається об’єднання так
і позначається об’єднання так 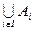 .
. . Якщо множин n штук:
. Якщо множин n штук:  , то позначення їх об’єднання буде
, то позначення їх об’єднання буде  , або
, або  .
. , перетин двох множин -
, перетин двох множин - 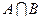 , перетин n множин -
, перетин n множин -  , або
, або 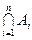 . Якщо множини не мають спільних елементів, то будемо казати, що їх перетин – порожня множина. Порожню множину будемо позначати символом Æ. Порожня множина може бути не тільки результатом перетину. Наприклад: множина дійсних розв’язків рівняння
. Якщо множини не мають спільних елементів, то будемо казати, що їх перетин – порожня множина. Порожню множину будемо позначати символом Æ. Порожня множина може бути не тільки результатом перетину. Наприклад: множина дійсних розв’язків рівняння  – порожня множина.
– порожня множина. . Різниця позначається так:
. Різниця позначається так:  .
. .
.
 тобто
тобто  і
і  , отже
, отже  для кожного
для кожного  і
і  . Навпаки, нехай
. Навпаки, нехай  і
і  для кожного
для кожного  .
. .
. .
. .
. тоді і тільки тоді, коли
тоді і тільки тоді, коли  .
. .
. .
. .
. , якщо
, якщо  і множини
і множини  не перетинаються.
не перетинаються. .
. .
. послідовності
послідовності  є множина
є множина  . Довести, що
. Довести, що  послідовності
послідовності  . Довести, що
. Довести, що  і писати
і писати  , або
, або  , при цьому елемент
, при цьому елемент  називається образом елементу
називається образом елементу  , а елемент
, а елемент  називається образом множини
називається образом множини  і позначається символом
і позначається символом  . Якщо при перетворенні
. Якщо при перетворенні  є образом деякого елементу
є образом деякого елементу  то кажуть, що
то кажуть, що  , або
, або 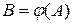 . Множина
. Множина  називається прообразом множини
називається прообразом множини  і позначається символом
і позначається символом 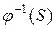 .
. кожної одно елементної множини
кожної одно елементної множини 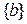 є відображення множини В на А, яке теж є взаємно однозначною відповідністю. Відображення
є відображення множини В на А, яке теж є взаємно однозначною відповідністю. Відображення  і
і  називаються взаємно оберненими.
називаються взаємно оберненими. ,
,  і
і  . Доведіть наступні співвідношення:
. Доведіть наступні співвідношення: ,
, ,
, .
. і
і  . Доведіть наступні співвідношення:
. Доведіть наступні співвідношення: ,
,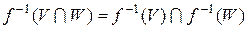 ,
, .
.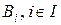 теж попарно не перетинаються і для будь якого
теж попарно не перетинаються і для будь якого  ~
~  , то
, то ~
~  .
. -довільна підмножина множини А, то
-довільна підмножина множини А, то  .
.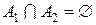 ,
,  і
і 

 , якщо
, якщо  , тобто
, тобто  ~
~  . Дійсно,
. Дійсно,  і
і  Отже
Отже  еквівалентна множині
еквівалентна множині  , а підмножина
, а підмножина  множини
множини  еквівалентна множині
еквівалентна множині  . Тоді
. Тоді  .
. і
і  . Тоді
. Тоді  .
. взаємно однозначне перетворення множини
взаємно однозначне перетворення множини 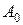 на
на  . Покладемо
. Покладемо  . З умови леми і означення множин
. З умови леми і означення множин  випливає їх монотонність:
випливає їх монотонність:  . Дійсно, для
. Дійсно, для  ,
,  це умова леми. Припустимо, що
це умова леми. Припустимо, що  , якщо
, якщо 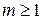 . Тоді
. Тоді  , тобто
, тобто  .
.

 . Оскільки
. Оскільки  (1.1.1)
(1.1.1) . (1.1.2)
. (1.1.2)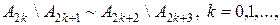 і доданки у правих частинах рівностей (1.1.1) - (1.1.2) попарно не перетинаються. Окрім того
і доданки у правих частинах рівностей (1.1.1) - (1.1.2) попарно не перетинаються. Окрім того  . Отже, внаслідок властивості 3 еквівалентних множин,
. Отже, внаслідок властивості 3 еквівалентних множин,  , де
, де 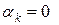 або 1.
або 1. і також називати двійковим дробом. Двійковий дріб виду
і також називати двійковим дробом. Двійковий дріб виду  , де
, де 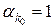 , називається двійково-раціональним числом. Ця сума дорівнює раціональному числу
, називається двійково-раціональним числом. Ця сума дорівнює раціональному числу  , де m непарне число менше за
, де m непарне число менше за 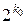 . Двійково-раціональне число
. Двійково-раціональне число  (запис (0) («0 в періоді») означає, що усі
(запис (0) («0 в періоді») означає, що усі  якщо
якщо  ) має зображення
) має зображення  .
. і не є двійково-раціональним числом. Необхідно побудувати
і не є двійково-раціональним числом. Необхідно побудувати  для будь-якого
для будь-якого  і довести, що частинна сума
і довести, що частинна сума 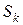 ряду
ряду 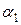 . Якщо
. Якщо  , покладемо
, покладемо  . Тоді
. Тоді  і
і  . Якщо
. Якщо  , то покладемо
, то покладемо  . Тоді
. Тоді  і
і  ,
,  . Знову розглянемо два випадки. Якщо
. Знову розглянемо два випадки. Якщо  , то покладемо
, то покладемо  .
. 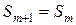 і
і  . Якщо
. Якщо  , то покладемо
, то покладемо  . Тоді
. Тоді 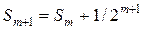 і
і  . Число
. Число  , тому що
, тому що 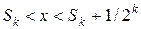 . З останній нерівності випливає
. З останній нерівності випливає  .
. множина всіх двійкових дробів,
множина всіх двійкових дробів,  множина усіх двійкових дробів, зображення яких містить нескінченну множину чисел
множина усіх двійкових дробів, зображення яких містить нескінченну множину чисел  множина всіх двійкових дробів, зображення яких містить одиницю в періоді.
множина всіх двійкових дробів, зображення яких містить одиницю в періоді. має потужність континуум, а множина
має потужність континуум, а множина  - множина потужності континууму.
- множина потужності континууму. всіх підмножин множини натуральних чисел є множиною потужності континууму.
всіх підмножин множини натуральних чисел є множиною потужності континууму. всіх підмножин будь-якої зчисленної множини
всіх підмножин будь-якої зчисленної множини  є множиною потужності континууму.
є множиною потужності континууму. , має потужність більшу, ніж континуум.
, має потужність більшу, ніж континуум.
 , якщо у будь-якому околу точки
, якщо у будь-якому околу точки  точок з
точок з  відстань від точки
відстань від точки 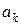 до
до  . Тоді в околу радіуса e ні буде не одної точка множини
. Тоді в околу радіуса e ні буде не одної точка множини  послідовність околів радіусу
послідовність околів радіусу  . Виберемо довільну точку
. Виберемо довільну точку  в околу
в околу 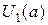 ,
,  в околу
в околу  , і так далі виберемо точку
, і так далі виберемо точку  , яка відрізняється від попередніх и точки
, яка відрізняється від попередніх и точки  , то послідовність точок
, то послідовність точок  є точки сегмента
є точки сегмента  .
. , будь-яка скінченна множина, множина усіх натуральних чисел
, будь-яка скінченна множина, множина усіх натуральних чисел  , множина усіх цілих чисел
, множина усіх цілих чисел  .
. називається внутрішньою точкою множини
називається внутрішньою точкою множини  називається відкритою, якщо кожна точка множини
називається відкритою, якщо кожна точка множини  внутрішня.
внутрішня. , об'єднання інтервалів.
, об'єднання інтервалів. , потім два інтервалу
, потім два інтервалу  , на
, на  му кроці вилучимо
му кроці вилучимо  інтервалів
інтервалів 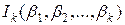 . Об’єднання усіх інтервалів
. Об’єднання усіх інтервалів 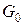 , а доповнення множини
, а доповнення множини  . За лемою 2.1.2 Канторова відкрита множина це множина усіх чисел з сегмента
. За лемою 2.1.2 Канторова відкрита множина це множина усіх чисел з сегмента  , трійковий запис яких неможливий без цифри 1. Наприклад, число (в трійковому запису) 0,1 має також вигляд 0,0(2), а тому воно не належить множині
, трійковий запис яких неможливий без цифри 1. Наприклад, число (в трійковому запису) 0,1 має також вигляд 0,0(2), а тому воно не належить множині  , де
, де  або 2, отже це множина потужності континууму. Обчислимо суму довжин вилучених інтервалів: Спочатку вилучається інтервал
або 2, отже це множина потужності континууму. Обчислимо суму довжин вилучених інтервалів: Спочатку вилучається інтервал  , потім два інтервала, довжина кожного з яких дорівнює
, потім два інтервала, довжина кожного з яких дорівнює  , на
, на  . Отже, сума довжин вилучених інтервалів дорівнює
. Отже, сума довжин вилучених інтервалів дорівнює
 відкритих множин називається покриттям множини
відкритих множин називається покриттям множини  , якщо
, якщо 
 відкритими множинами можна виділити скінченнне покриття.
відкритими множинами можна виділити скінченнне покриття.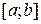 , що містить множину
, що містить множину  . Тоді хоча б для одної з замкнених множин
. Тоді хоча б для одної з замкнених множин  або
або  не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через
не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через  , а сегмент, в якому вона міститься через
, а сегмент, в якому вона міститься через  . Очевидно, що
. Очевидно, що  і довжина сегмента
і довжина сегмента  =1/2
=1/2  . Нехай побудована послідовність вкладених сегментів
. Нехай побудована послідовність вкладених сегментів  таких, що для множин
таких, що для множин  неможливо вилучити скінченнне покриття,
неможливо вилучити скінченнне покриття,  , а також
, а також  =
=  . Нехай
. Нехай 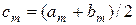 . Тоді хоча б для одної з замкнених множин
. Тоді хоча б для одної з замкнених множин  або
або  не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через
не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через  , а сегмент, в якому вона міститься через
, а сегмент, в якому вона міститься через  .
. , довжини яких прямують до нуля, і послідовність вкладених замкнених множин
, довжини яких прямують до нуля, і послідовність вкладених замкнених множин  , таких, що для кожної з них неможливо вилучити скінченнне покриття.
, таких, що для кожної з них неможливо вилучити скінченнне покриття. . Тоді точка
. Тоді точка 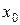 є граничною точкою замкненої множини
є граничною точкою замкненої множини  - відкрита множина з даного покриття, що містить точку
- відкрита множина з даного покриття, що містить точку  . Якщо
. Якщо 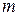 таке, що
таке, що  , то усі сегменти
, то усі сегменти  за умовою, що
за умовою, що  . Отже всі множини
. Отже всі множини  покриваються відкритою множиною
покриваються відкритою множиною  .
.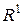
 збігається з
збігається з  , тобто
, тобто  .
. , то в силу властивості 2 міри елементарних множин,
, то в силу властивості 2 міри елементарних множин,  і слід
і слід  . З іншого боку
. З іншого боку  тому, що
тому, що  , то
, то  .
.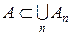 , де
, де 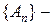 скінченна, або зчисленна сім’я множин, то
скінченна, або зчисленна сім’я множин, то  .
. і довільного числа
і довільного числа 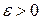 знайдеться скінченна, або зчисленна система елементарних множин
знайдеться скінченна, або зчисленна система елементарних множин  така, що
така, що  і
і  . Тоді
. Тоді  і
і .
. . (3.3.2)
. (3.3.2) і попередню властивість, одержимо
і попередню властивість, одержимо  . Помінявши місцями
. Помінявши місцями  і отже маємо (3.3.2).
і отже маємо (3.3.2). .
. . Міра позначається символом
. Міра позначається символом  і називається мірою Лебега.
і називається мірою Лебега. .
. .
. .
.


