
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зліченні множини та їх властивості.Содержание книги
Поиск на нашем сайте
Означення. Множина називається зліченною, якщо вона рівнопотужна множині натуральних чисел. Тобто елементи зліченної множини можна перенумерувати. Приклади 1, 2 з попереднього параграф показують, що множини парних та непарних натуральних чисел – зліченні. Теорема. Множина Доведення. Встановимо взаємно однозначну відповідність між множинами
Тим самим зліченність множини Зліченні множини мають наступні властивості. Властивість 1. Будь яка нескінченна множина має зліченну підмножину. Доведення. Нехай
З цієї властивості випливає, що зліченна множина є «найменшою» серед нескінченних множин. Тобто, якщо множина нескінченна, то вона принаймні зліченна. Властивість 2. Об’єднання зліченної та скінченної множини є множина зліченна. Доведення. Нехай
Нехай
Запишемо множину
Тепер легко встановити взаємно однозначну відповідність між множинами
Отже Властивість 3. Об’єднання двох зліченних множин є множина зліченна. Доведення. Нехай
Запишемо
Тепер легко встановити взаємно однозначну відповідність між множинами
Отже Властивість 4. Об’єднання скінченного числа зліченних множин є множина зліченна. Доведення здійснимо методом математичної індукції. Нехай Властивість 5. Об’єднання зліченного числа зліченних множин є множина зліченна.
Доведення. Розглянемо зліченні множини:
…
… Запишемо об’єднання
У кожній групі, що взята у дужки, виписуються елементи, сума індексів яких дорівнює номеру групи, збільшеному на 1. З цього видно, що дана множина зліченна. Дійсно:
Пропонована нумерація має просту геометричну інтерпретацію:
Наслідок. Множина Доведення. Доведемо спочатку зліченність множини додатних раціональних чисел. Кожне з таких чисел має вигляд
...
…
Деякі числа будуть повторюватись (наприклад,
Потужність континууму.
Не всі нескінченні множини є зліченними. Покажемо, що, наприклад, множина дійсних чисел, що лежать в інтервалі Теорема. Множина дійсних чисел з інтервалу Доведення. Кожне дійсне число з інтервалу
Доведемо теорему методом від протилежного. Припустимо, що дійсні числа з інтервалу
Означення. Будь яка множина, рівнопотужна множині дійсних чисел з інтервалу (0,1), називається множиною потужності континуума (від лат. continuum – неперервність). Такі множини, на відміну від зліченних множин, складаються не з дискретної множини точок, а є об’єднанням суцільних інтервалів або областей. З розглянутих у п. 5 прикладів випливає, що множина точок будь якого відрізку або інтервалу, множина точок всієї числової прямої (а отже множина дійсних чисел Цікаве питання – чи існують множини, потужність яких була б проміжною між зліченністю та континуумом? Існує гіпотеза, яка полягає в тому, що таких множин нема. Ця гіпотеза називається гіпотезою континууму.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 2066; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.23.83 (0.009 с.) |

 цілих чисел – зліченна.
цілих чисел – зліченна. наступним чином:
наступним чином: .
. – довільна нескінченна множина. Оберемо який-небудь елемент з множини
– довільна нескінченна множина. Оберемо який-небудь елемент з множини  . В множині
. В множині  . Цей процес можна продовжувати необмежено – після кожного обирання елементу з множини
. Цей процес можна продовжувати необмежено – після кожного обирання елементу з множини  , яка є підмножиною множини
, яка є підмножиною множини  – зліченна множина. Тоді її елементи можна перенумерувати, і цю множину подати у вигляді:
– зліченна множина. Тоді її елементи можна перенумерувати, і цю множину подати у вигляді: .
. – скінченна множина:
– скінченна множина: .
. наступним чином:
наступним чином: .
. .
. .
. .
. .
. – зліченні множини. Якщо
– зліченні множини. Якщо  , то твердження справедливе (властивість 3). Припустимо, що твердження справедливе для
, то твердження справедливе (властивість 3). Припустимо, що твердження справедливе для  , тобто множина
, тобто множина 
 – зліченна. Покажемо, що твердження справедливе для
– зліченна. Покажемо, що твердження справедливе для  , тобто множина
, тобто множина  – зліченна. Дійсно:
– зліченна. Дійсно:  – зліченна множина (на підставі властивості 3).
– зліченна множина (на підставі властивості 3). ,
, ,
, ,
, ,
, наступним чином:
наступним чином:
 .
.


 раціональних чисел зліченна.
раціональних чисел зліченна. , де
, де  . Випишемо спочатку всі такі числа, знаменник яких дорівнює 1, потім всі, знаменник яких дорівнює 2, тощо:
. Випишемо спочатку всі такі числа, знаменник яких дорівнює 1, потім всі, знаменник яких дорівнює 2, тощо:




 тощо). Застосовуючи метод, який було використано при доведенні властивості 5, і, викреслюючи скоротні дроби, отримаємо зліченність множини додатних раціональних чисел. Зліченність множини від’ємних раціональних чисел доводиться аналогічно. Множина всіх раціональних чисел є об’єднанням множин додатних раціональних чисел, множини від’ємних раціональних чисел і множини
тощо). Застосовуючи метод, який було використано при доведенні властивості 5, і, викреслюючи скоротні дроби, отримаємо зліченність множини додатних раціональних чисел. Зліченність множини від’ємних раціональних чисел доводиться аналогічно. Множина всіх раціональних чисел є об’єднанням множин додатних раціональних чисел, множини від’ємних раціональних чисел і множини  . На підставі властивостей 2 і 3 отримаємо зліченність множини всіх раціональних чисел.
. На підставі властивостей 2 і 3 отримаємо зліченність множини всіх раціональних чисел. , зліченною не є.
, зліченною не є. , де хоча б одна з цифр
, де хоча б одна з цифр  відмінна від нуля. Дійсно, якщо всі
відмінна від нуля. Дійсно, якщо всі 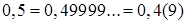 .
. відповідає число
відповідає число  . Побудуємо число
. Побудуємо число  , де
, де  . Таке число не співпадає з жодним з чисел
. Таке число не співпадає з жодним з чисел  , оскільки відрізняється від нього принаймні однією цифрою (
, оскільки відрізняється від нього принаймні однією цифрою ( ). Але
). Але  ) мають потужність континууму. Потужність континууму мають також множина точок площини, простору.
) мають потужність континууму. Потужність континууму мають також множина точок площини, простору.


