Властивості функцій, неперервних на відрізку.
Означення. Функція  називається неперервною на множині називається неперервною на множині  , якщо вона неперервна в кожній точці множини , якщо вона неперервна в кожній точці множини  . .
Зокрема, функція  називається неперервною на інтервалі називається неперервною на інтервалі  , якщо вона неперервна в кожній точці інтервалу , якщо вона неперервна в кожній точці інтервалу  . Функція . Функція  називається неперервною на відрізку називається неперервною на відрізку  , якщо вона неперервна на інтервалі , якщо вона неперервна на інтервалі  , і, крім того, неперервна справа в точці , і, крім того, неперервна справа в точці  і неперервна зліва в точці і неперервна зліва в точці  . .
З’ясовується, що властивості функцій, неперервних на відрізку, суттєво відрізняються від властивостей функцій, неперервних тільки на інтервалі або півінтервалі.
Перша теорема Вейєрштрасса. Якщо функція  неперервна на відрізку неперервна на відрізку  , то вона обмежена на відрізку , то вона обмежена на відрізку  . .
Доведення. Припустимо протилежне, тобто припустимо, що 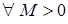   . Зокрема, якщо . Зокрема, якщо  , то , то   . Якщо . Якщо  , то , то  . І взагалі . І взагалі   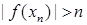 . .
Послідовність  обмежена, оскільки всі її елементи належать відрізку обмежена, оскільки всі її елементи належать відрізку  . За лемою Больцано–Вейєрштрасса з неї можна виділити збіжну підпослідовність . За лемою Больцано–Вейєрштрасса з неї можна виділити збіжну підпослідовність  : : 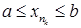 , і , і  . Але тоді . Але тоді  (наслідок 3 з теореми 4, п. 10). Оскільки функція (наслідок 3 з теореми 4, п. 10). Оскільки функція  неперервна на відрізку неперервна на відрізку  , отже і в точці , отже і в точці  , то , то
 . (23.1) . (23.1)
Але  . Оскільки . Оскільки  , то , то  , що суперечить (23.1). , що суперечить (23.1).
Теорему доведено.
З геометричної точки зору ця теорема означає, що графік неперервної на відрізку функції цілком міститься всередині деякого прямокутника (рис. 45).

Рис. 45.
Зауваження. Твердження теореми втрачає силу, якщо відрізок замінити інтервалом або півінтервалом. Наприклад, функція  неперервна на інтервалі неперервна на інтервалі  , але не є на ньому обмеженою. , але не є на ньому обмеженою.
Друга теорема Вейєрштрасса. Якщо функція  неперервна на відрізку неперервна на відрізку  , то вона досягає на цьому відрізку своїх точних верхньої та нижньої граней. , то вона досягає на цьому відрізку своїх точних верхньої та нижньої граней.
Доведення. Оскільки функція  неперервна на відрізку неперервна на відрізку  , то вона обмежена на відрізку , то вона обмежена на відрізку  , отже функція , отже функція  має на цьому відрізку точні верхню та нижню грань. Позначимо: має на цьому відрізку точні верхню та нижню грань. Позначимо:  . Припустимо всупереч твердженню теореми, що . Припустимо всупереч твердженню теореми, що 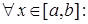  . Розглянемо функцію: . Розглянемо функцію:
 . .
Оскільки 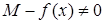 , то функція , то функція  неперервна на відрізку неперервна на відрізку  , отже функція , отже функція  обмежена на відрізку обмежена на відрізку  , тобто , тобто  таке, що таке, що  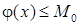 . Отже . Отже
 , ,
звідки випливає, що
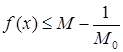 . .
А це означає, що  . Таким чином ми довели, що . Таким чином ми довели, що   , тобто функція , тобто функція  досягає на відрізку досягає на відрізку  своєї верхньої грані. Аналогічно доводиться, що функція своєї верхньої грані. Аналогічно доводиться, що функція  досягає на відрізку досягає на відрізку  своєї нижньої грані. своєї нижньої грані.
Теорема доведено.
Зауваження. Твердження і цієї теореми втрачає силу, якщо відрізок замінити інтервалом, або півінтервалом. Наприклад, функція  неперервна на інтервалі неперервна на інтервалі  , але не досягає на цьому інтервалі своєї точної нижньої грані, яка дорівнює нулю, і своєї точної верхньої грані, яка дорівнює 1. , але не досягає на цьому інтервалі своєї точної нижньої грані, яка дорівнює нулю, і своєї точної верхньої грані, яка дорівнює 1.
Перша теорема Больцано–Коші (про корінь). Нехай функція  неперервна на відрізку неперервна на відрізку  , і на кінцях цього відрізку приймає значення різних знаків, тобто , і на кінцях цього відрізку приймає значення різних знаків, тобто  . Тоді . Тоді   . .
Доведення. Поділимо відрізок  навпіл. Позначимо: навпіл. Позначимо:
 . .
Якщо  , то теорему доведено. Якщо , то теорему доведено. Якщо  , то з двох відрізків , то з двох відрізків  та та 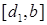 оберемо той, на кінцях якого функція оберемо той, на кінцях якого функція  приймає значення різних знаків. Позначимо його як приймає значення різних знаків. Позначимо його як  . Його довжина: . Його довжина:
 . .
Тепер відрізок  також поділимо навпіл. Позначимо: також поділимо навпіл. Позначимо:
 . .
Якщо  , то теорему доведено. Якщо , то теорему доведено. Якщо  , то з двох відрізків , то з двох відрізків 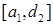 та та  обираємо той, на кінцях якого функція обираємо той, на кінцях якого функція  приймає значення різних знаків. Позначимо його як приймає значення різних знаків. Позначимо його як  . Його довжина: . Його довжина:
 . .
Продовжуючи цей процес, ми отримаємо, що або на деякому кроці знайдеться точка  така, що така, що  , або вийде послідовність вкладених відрізків , або вийде послідовність вкладених відрізків  , причому , причому  , і , і
 . .
Таким чином ця послідовність відрізків є стяжною. За теоремою Кантора (див. п. 12) існує така точка  , яка належить всім цим відрізкам. Покажемо, що , яка належить всім цим відрізкам. Покажемо, що  . Дійсно, нехай, наприклад . Дійсно, нехай, наприклад  . Тоді, оскільки функція . Тоді, оскільки функція  неперервна, то неперервна, то  таке, що таке, що  виконано виконано  . З іншого боку, оскільки . З іншого боку, оскільки
 , то для цього , то для цього  знайдеться такий номер знайдеться такий номер  , що , що  . В той же час . В той же час 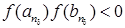 , що суперечить тому, що , що суперечить тому, що  . Отже залишається тільки можливість, коли . Отже залишається тільки можливість, коли  . .
Теорему доведено.
Геометричну ілюстрацію теореми наведено на рис. 46. Графік неперервної на відрізку функції, яка на його кінцях приймає значення різних знаків, перетинає вісь 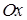 хоча б в одній точці цього відрізку. хоча б в одній точці цього відрізку.

Рис. 46.
Точка  називається коренем рівняння називається коренем рівняння  . Сформульована теорема тільки стверджує існування кореня, але не вказує, як його знайти. тем не менш, використовуючи цю теорему, можна знайти корінь наближено. . Сформульована теорема тільки стверджує існування кореня, але не вказує, як його знайти. тем не менш, використовуючи цю теорему, можна знайти корінь наближено.
Розглянемо приклад.
Довести, що на відрізку  рівняння рівняння 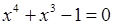 має корінь, і знайти цей корінь з точністю 0,1. має корінь, і знайти цей корінь з точністю 0,1.
Нехай 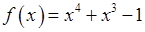 . Ця функція неперервна на всій числовій прямій, отже і на відрізку . Ця функція неперервна на всій числовій прямій, отже і на відрізку  . Оскільки . Оскільки  , то за першою теоремою Больцано–Коші на відрізку , то за першою теоремою Больцано–Коші на відрізку  дане рівняння має корінь. Поділимо точкою дане рівняння має корінь. Поділимо точкою  відрізок відрізок  навпіл і з двох отриманих відрізків навпіл і з двох отриманих відрізків  і і  оберемо той, на кінцях якого функція оберемо той, на кінцях якого функція  набуває значень різних знаків. Оскільки набуває значень різних знаків. Оскільки  , то це відрізок , то це відрізок  . Отже знову за тою ж теоремою на ньому є корінь нашого рівняння. Далі точкою . Отже знову за тою ж теоремою на ньому є корінь нашого рівняння. Далі точкою  ділимо цей відрізок навпіл і знову з двох отриманих відрізків ділимо цей відрізок навпіл і знову з двох отриманих відрізків  і і  обираємо той, на кінцях якого функція набуває значень різних знаків. Оскільки обираємо той, на кінцях якого функція набуває значень різних знаків. Оскільки  , то це відрізок , то це відрізок  . Продовжуючи цей процес, далі знаходимо: . Продовжуючи цей процес, далі знаходимо: 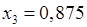 ; ;  . Обираємо далі відрізок . Обираємо далі відрізок  . Довжина цього відрізку 0,875-0,75=0,125. Отже, якщо у якості наближеного значення кореня взяти точку . Довжина цього відрізку 0,875-0,75=0,125. Отже, якщо у якості наближеного значення кореня взяти точку  , яка ділить відрізок , яка ділить відрізок  навпіл, то отримаємо: навпіл, то отримаємо:  , тобто необхідну точність досягнено. Отже , тобто необхідну точність досягнено. Отже 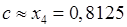 . Значення функції . Значення функції  у цій точці: у цій точці:  . .
Продовжуючи цей процес, можна знайти корінь з будь якою наперед заданою точністю. Але навіть з цього прикладу можна помітити, що для досягнення точності 0,1 ми змушені зробити 4 кроки. А більшість прикладних задач вимагає значно вищої точності. Припустимо, що нам треба знайти корінь з деякою точністю  . Тоді неважко переконатися, що кількість кроків . Тоді неважко переконатися, що кількість кроків 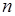 , яка необхідна для досягнення цієї точності, повинна задовольнять нерівність: , яка необхідна для досягнення цієї точності, повинна задовольнять нерівність:
 , тобто , тобто  . Наприклад, для досягнення точності . Наприклад, для досягнення точності  треба зробити 10 кроків. Тому на практиці частіше використовують інші, більш потужні методи знаходження коренів рівнянь, наприклад, так званий метод Ньютона. треба зробити 10 кроків. Тому на практиці частіше використовують інші, більш потужні методи знаходження коренів рівнянь, наприклад, так званий метод Ньютона.
Друга теорема Больцано–Коші (про проміжне значення). Нехай функція  неперервна на відрізку неперервна на відрізку  , причому , причому  , ,  , і , і 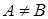 . Тоді для будь якого значення . Тоді для будь якого значення 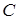 , яке лежить між , яке лежить між  і і  , знайдеться , знайдеться  таке, що таке, що  . .
Доведення. Припустимо для визначеності, що 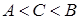 . Введемо допоміжну функцію . Введемо допоміжну функцію 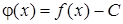 . Ця функція неперервна на відрізку . Ця функція неперервна на відрізку  як різниця двох неперервних функцій. Крім того, як різниця двох неперервних функцій. Крім того,  , ,  , тобто на кінцях відрізку , тобто на кінцях відрізку  функція функція  приймає значення різних знаків. Тоді згідно з попередньою теоремою знайдеться приймає значення різних знаків. Тоді згідно з попередньою теоремою знайдеться  таке, що таке, що  , тобто , тобто  . .
Теорему доведено.
Ця теорема стверджує, що неперервна на відрізку функція при переході від одного значення до іншого набуває всіх проміжних між ними значень.
Геометричну ілюстрацію теореми наведено на рис. 47.

Рис. 47.
Теорема (про неперервність оберненої функції). Якщо функція  неперервна та зростаюча на відрізку неперервна та зростаюча на відрізку  , причому , причому  , ,  , то на відрізку , то на відрізку  визначено функцію визначено функцію  , яка є оберненою до функції , яка є оберненою до функції  , і яка неперервна та зростаюча на відрізку , і яка неперервна та зростаюча на відрізку  . .
Доведення. Оскільки функція  зростаюча, то зростаюча, то  виконано: виконано:  , причому , причому  , ,  . Таким чином множиною значень на відрізку . Таким чином множиною значень на відрізку  функції функції  є відрізок є відрізок  . .
Згідно означенню оберненої функції (див. п. 16), треба довести, що для кожного 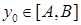 існує єдине значення існує єдине значення  таке, що таке, що 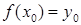 . Існування значення . Існування значення  випливає з теореми про проміжне значення. Доведемо, що таке значення єдине. Припустимо, що існує ще одне значення випливає з теореми про проміжне значення. Доведемо, що таке значення єдине. Припустимо, що існує ще одне значення  таке, що таке, що  , причому , причому  . Якщо . Якщо  , то внаслідок зростання функції , то внаслідок зростання функції  на відрізку на відрізку  має бути має бути  , що неможливо, оскільки , що неможливо, оскільки  . Аналогічно виключається можливість . Аналогічно виключається можливість 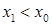 , тобто може бути тільки , тобто може бути тільки 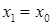 . Таким чином існування оберненої функції . Таким чином існування оберненої функції  доведено. Покажемо, що ця функція зростаюча на відрізку доведено. Покажемо, що ця функція зростаюча на відрізку  . Розглянемо два значення . Розглянемо два значення 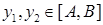 , такі, що , такі, що  . Треба показати, що . Треба показати, що  . Припустимо, що це не так, тобто . Припустимо, що це не так, тобто  . Позначимо: . Позначимо:  , ,  . Тоді . Тоді  , причому , причому  . Оскільки функція . Оскільки функція  зростаюча на відрізку зростаюча на відрізку  , то звідси , то звідси 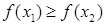 , тобто , тобто  , що суперечить тому, що , що суперечить тому, що  . Таким чином функція . Таким чином функція  зростаюча на відрізку зростаюча на відрізку  . Залишилося довести, що ця функція неперервна на відрізку . Залишилося довести, що ця функція неперервна на відрізку  . Нехай . Нехай  – довільна точка інтервалу – довільна точка інтервалу 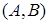 . Покажемо, що функція . Покажемо, що функція  неперервна в точці неперервна в точці  . Для цього достатньо показати справедливість рівностей: . Для цього достатньо показати справедливість рівностей:
 . (23.1) . (23.1)
За теоремою про границю монотонної функції (див. п. 21) існують границі 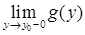 , ,  , і виконується подвійна нерівність: , і виконується подвійна нерівність:
 . (23.2) . (23.2)
Нехай хоча б одна з рівностей (23.1) не виконується, наприклад  . Тоді . Тоді
 . (23.3) . (23.3)
Оскільки  виконано виконано  , причому , причому  , і , і  виконано виконано 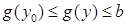 , то з (23.3) випливає, що інтервал , то з (23.3) випливає, що інтервал  не належить множині значень функції не належить множині значень функції  . Це суперечить тому, що всі точки відрізку . Це суперечить тому, що всі точки відрізку  , в тому числі і точки інтервалу , в тому числі і точки інтервалу  належать множині належать множині 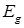 . Аналогічно доводиться справедливість другої з рівностей (23.1), тобто . Аналогічно доводиться справедливість другої з рівностей (23.1), тобто  . .
Тим же способом встановлюється, що функція  неперервна справа в точці неперервна справа в точці  і неперервна зліва в точці і неперервна зліва в точці  . .
Теорему доведено.
Зауваження 1. Якщо функція  спадна на відрізку спадна на відрізку  , то функція , то функція  спадна на відрізку спадна на відрізку  . .
Зауваження 2. Аналогічним чином формулюються та доводяться теореми про обернену функцію, коли функція  задана на інтервалі або півінтервалі. задана на інтервалі або півінтервалі.
Якщо функція  визначена, зростаюча та неперервна на інтервалі визначена, зростаюча та неперервна на інтервалі  , то обернена функція , то обернена функція  визначена, зростаюча та неперервна на інтервалі визначена, зростаюча та неперервна на інтервалі 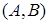 , де , де  , ,  . .
|



 називається неперервною на множині
називається неперервною на множині  , якщо вона неперервна в кожній точці множини
, якщо вона неперервна в кожній точці множини  , якщо вона неперервна в кожній точці інтервалу
, якщо вона неперервна в кожній точці інтервалу  , якщо вона неперервна на інтервалі
, якщо вона неперервна на інтервалі  і неперервна зліва в точці
і неперервна зліва в точці  .
.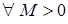

 . Зокрема, якщо
. Зокрема, якщо  , то
, то 
 . Якщо
. Якщо  , то
, то  . І взагалі
. І взагалі 

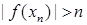 .
. обмежена, оскільки всі її елементи належать відрізку
обмежена, оскільки всі її елементи належать відрізку  :
: 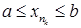 , і
, і  . Але тоді
. Але тоді  (наслідок 3 з теореми 4, п. 10). Оскільки функція
(наслідок 3 з теореми 4, п. 10). Оскільки функція  , то
, то . (23.1)
. (23.1) . Оскільки
. Оскільки  , то
, то  , що суперечить (23.1).
, що суперечить (23.1).
 неперервна на інтервалі
неперервна на інтервалі  , але не є на ньому обмеженою.
, але не є на ньому обмеженою. . Припустимо всупереч твердженню теореми, що
. Припустимо всупереч твердженню теореми, що 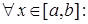
 . Розглянемо функцію:
. Розглянемо функцію: .
.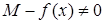 , то функція
, то функція  неперервна на відрізку
неперервна на відрізку  таке, що
таке, що 
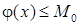 . Отже
. Отже ,
,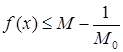 .
. . Таким чином ми довели, що
. Таким чином ми довели, що 
 , тобто функція
, тобто функція  неперервна на інтервалі
неперервна на інтервалі  . Тоді
. Тоді 
 .
. .
. , то теорему доведено. Якщо
, то теорему доведено. Якщо  , то з двох відрізків
, то з двох відрізків  та
та 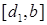 оберемо той, на кінцях якого функція
оберемо той, на кінцях якого функція  . Його довжина:
. Його довжина: .
. .
. , то теорему доведено. Якщо
, то теорему доведено. Якщо  , то з двох відрізків
, то з двох відрізків 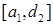 та
та  обираємо той, на кінцях якого функція
обираємо той, на кінцях якого функція  . Його довжина:
. Його довжина: .
. така, що
така, що  , або вийде послідовність вкладених відрізків
, або вийде послідовність вкладених відрізків  , причому
, причому  , і
, і .
. . Тоді, оскільки функція
. Тоді, оскільки функція  таке, що
таке, що  виконано
виконано  . З іншого боку, оскільки
. З іншого боку, оскільки , то для цього
, то для цього  знайдеться такий номер
знайдеться такий номер  , що
, що  . В той же час
. В той же час 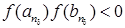 , що суперечить тому, що
, що суперечить тому, що 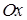 хоча б в одній точці цього відрізку.
хоча б в одній точці цього відрізку.
 називається коренем рівняння
називається коренем рівняння  . Сформульована теорема тільки стверджує існування кореня, але не вказує, як його знайти. тем не менш, використовуючи цю теорему, можна знайти корінь наближено.
. Сформульована теорема тільки стверджує існування кореня, але не вказує, як його знайти. тем не менш, використовуючи цю теорему, можна знайти корінь наближено. рівняння
рівняння 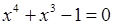 має корінь, і знайти цей корінь з точністю 0,1.
має корінь, і знайти цей корінь з точністю 0,1.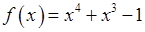 . Ця функція неперервна на всій числовій прямій, отже і на відрізку
. Ця функція неперервна на всій числовій прямій, отже і на відрізку  , то за першою теоремою Больцано–Коші на відрізку
, то за першою теоремою Больцано–Коші на відрізку  відрізок
відрізок  і
і  оберемо той, на кінцях якого функція
оберемо той, на кінцях якого функція  набуває значень різних знаків. Оскільки
набуває значень різних знаків. Оскільки  , то це відрізок
, то це відрізок  ділимо цей відрізок навпіл і знову з двох отриманих відрізків
ділимо цей відрізок навпіл і знову з двох отриманих відрізків  і
і  обираємо той, на кінцях якого функція набуває значень різних знаків. Оскільки
обираємо той, на кінцях якого функція набуває значень різних знаків. Оскільки  , то це відрізок
, то це відрізок 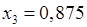 ;
;  . Обираємо далі відрізок
. Обираємо далі відрізок  . Довжина цього відрізку 0,875-0,75=0,125. Отже, якщо у якості наближеного значення кореня взяти точку
. Довжина цього відрізку 0,875-0,75=0,125. Отже, якщо у якості наближеного значення кореня взяти точку  , яка ділить відрізок
, яка ділить відрізок  , тобто необхідну точність досягнено. Отже
, тобто необхідну точність досягнено. Отже 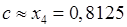 . Значення функції
. Значення функції  .
. . Тоді неважко переконатися, що кількість кроків
. Тоді неважко переконатися, що кількість кроків 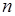 , яка необхідна для досягнення цієї точності, повинна задовольнять нерівність:
, яка необхідна для досягнення цієї точності, повинна задовольнять нерівність: , тобто
, тобто  . Наприклад, для досягнення точності
. Наприклад, для досягнення точності  треба зробити 10 кроків. Тому на практиці частіше використовують інші, більш потужні методи знаходження коренів рівнянь, наприклад, так званий метод Ньютона.
треба зробити 10 кроків. Тому на практиці частіше використовують інші, більш потужні методи знаходження коренів рівнянь, наприклад, так званий метод Ньютона. ,
,  , і
, і 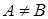 . Тоді для будь якого значення
. Тоді для будь якого значення 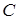 , яке лежить між
, яке лежить між  і
і  , знайдеться
, знайдеться  таке, що
таке, що  .
.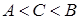 . Введемо допоміжну функцію
. Введемо допоміжну функцію 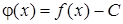 . Ця функція неперервна на відрізку
. Ця функція неперервна на відрізку  ,
,  , тобто на кінцях відрізку
, тобто на кінцях відрізку  , тобто
, тобто 
 визначено функцію
визначено функцію  , яка є оберненою до функції
, яка є оберненою до функції  виконано:
виконано:  , причому
, причому  ,
,  . Таким чином множиною значень на відрізку
. Таким чином множиною значень на відрізку  .
.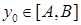 існує єдине значення
існує єдине значення  таке, що
таке, що 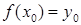 . Існування значення
. Існування значення  випливає з теореми про проміжне значення. Доведемо, що таке значення єдине. Припустимо, що існує ще одне значення
випливає з теореми про проміжне значення. Доведемо, що таке значення єдине. Припустимо, що існує ще одне значення  таке, що
таке, що  , причому
, причому  . Якщо
. Якщо  , то внаслідок зростання функції
, то внаслідок зростання функції  , що неможливо, оскільки
, що неможливо, оскільки  . Аналогічно виключається можливість
. Аналогічно виключається можливість 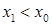 , тобто може бути тільки
, тобто може бути тільки 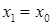 . Таким чином існування оберненої функції
. Таким чином існування оберненої функції 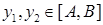 , такі, що
, такі, що  . Треба показати, що
. Треба показати, що  . Припустимо, що це не так, тобто
. Припустимо, що це не так, тобто  . Позначимо:
. Позначимо:  ,
,  . Тоді
. Тоді  , причому
, причому  . Оскільки функція
. Оскільки функція 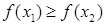 , тобто
, тобто  , що суперечить тому, що
, що суперечить тому, що  – довільна точка інтервалу
– довільна точка інтервалу 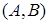 . Покажемо, що функція
. Покажемо, що функція  . (23.1)
. (23.1)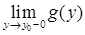 ,
,  , і виконується подвійна нерівність:
, і виконується подвійна нерівність: . (23.2)
. (23.2) . Тоді
. Тоді . (23.3)
. (23.3) виконано
виконано  , причому
, причому  , і
, і  виконано
виконано 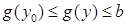 , то з (23.3) випливає, що інтервал
, то з (23.3) випливає, що інтервал  не належить множині значень функції
не належить множині значень функції  належать множині
належать множині  . Аналогічно доводиться справедливість другої з рівностей (23.1), тобто
. Аналогічно доводиться справедливість другої з рівностей (23.1), тобто  .
. ,
,  .
.


