
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числова вісь, проміжки на ній. Модуль дійсного числа.Содержание книги
Поиск на нашем сайте
У математиці виключно важливу роль відіграють числові множини, тобто такі, елементами яких є числа. Розглянемо найбільш важливі з них. Множина натуральних чисел
2. Множина цілих чисел Цілі числа мають низку дуже цікавих властивостей. Дослідженню цих властивостей присвячено такий розділ математики, як теорія чисел. Видатний німецький математик К.Ф. Гаус вважав теорію чисел царицею математики. Частка від ділення двох цілих чисел не завжди є цілим числом, наприклад 3. Множина раціональних чисел Раціональним ми називаємо число, яке можна зобразити у вигляді частки двох цілих чисел:
Сума, добуток, різниця і частка двох раціональних чисел є також число раціональне. Між будь якими двома раціональними числами завжди знайдеться принаймні ще одне (а отже нескінченна кількість) раціональних чисел. Дійсно, якщо Довгий час математики вважали, що раціональні числа вичерпують собою всі можливі числа. Деякі підстави у них для цього були: за допомогою раціональних чисел розв’язувалися практично всі задачі того часу. Представники філософської школи Піфагора вважали, що саме раціональне число лежить в основі світу. На підставі властивостей раціональних чисел ними, зокрема, була побудована теорія гармонії. Але потім виявилось, що існують задачі, розв’язання яких потребує виходу за межі множини раціональних чисел. Розглянемо таку задачу: знайти гіпотенузу
Ми можемо також вважати, що дріб Оскільки Таким чином ми довели, що число 3. Множина дійсних чисел Об’єднання множин раціональних та ірраціональних чисел складає множину дійсних чисел. На цій множині визначено операції додавання, віднімання, множення, ділення (крім ділення на нуль), і результат цих операцій теж число дійсне. Не можна на множині Будь яке раціональне число можна зобразити у вигляді скінченного, або нескінченного періодичного десяткового дробу. Наприклад:
Ірраціональне число зображується нескінченним неперіодичним десятковим дробом:
У загальному випадку кожне дійсне число можна подати у вигляді нескінченного десяткового дробу (періодичного або неперіодичного):
Якщо ми обірвемо цей дріб на
Припустимо, що
Очевидна подвійна нерівність:
Таким чином кожне дійсне число міститься між двома раціональними числами, різниця між якими дорівнює Нехай
Звідси випливає наступне твердження:
Іншими словами, будь яке дійсне число можна з будь якою степеню точності наблизити раціональним числом. Дійсні числа мають зручну геометричну інтерпретацію. Введемо наступне поняття. Числовою віссю називається пряма лінія, на якій обрано напрям, який умовно вважається додатним, початок відліку (точка 0) і одиниця ділення (рис. 5).
Рис. 5.
Тоді будь якому дійсному числу
Рис. 6.
Таким чином між множиною дійсних чисел Нехай Відрізком (сегментом) Інтервалом Півсегментом (півінтервалом) Суттєвою відмінністю відрізка Інтервали та півінтервали, зокрема, можуть бути і нескінченними: Нехай Наприклад, інтервали
Рис. 7.
Задамо тепер дійсне число Означення. Тепер вже точка
Рис. 8.
Нехай задано дійсне число Означення. Модулем (абсолютною величиною) числа
Наприклад: З геометричної точки зору
Рис. 9
Сформулюємо найбільш важливі властивості модуля: 1) 2) 3) 4) 5) 6) 7) 8)
Нехай
Рис. 10.
Розглянемо
Рис. 11
Тоді очевидно, що Виключимо з околу Означення. Цілою частиною дійсного числа Ціла частина числа
Число Означення. Дробовою частиною дійсного числа Позначається дробова частина числа
Отже
Аксіоми дійсних чисел.
Дійсні числа підпорядковуються наступним аксіомам. I. 1) 2) 3) 4) II. 1) 2) 3) 4) III. IV. Упорядкованість. V. Неперервність. Для будь яких непорожніх множин
Обмежені множини.
Означення. Множина Означення. Множина Число Наприклад, множина від’ємних чисел обмежена зверху, оскільки для будь якого від’ємного числа Зрозуміло, що якщо множина Означення. Найменша з верхніх граней множини Якщо 1) 2) Якщо 1) 2) Супремум та інфімум множини можуть належати цій множині, а можуть й не належати. Наприклад, якщо З означення точної верхньої грані випливає, що якщо множина Теорема. Якщо множина Доведення. Нехай непорожня множина
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1001; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.235.195 (0.008 с.) |

 . Це числа, які ми використовуємо при рахуванні предметів. Множина
. Це числа, які ми використовуємо при рахуванні предметів. Множина  нескінченна, тобто
нескінченна, тобто  . Сума і добуток двох натуральних чисел також число натуральне. А ось різниця двох натуральних чисел не завжди є числом натуральним, наприклад
. Сума і добуток двох натуральних чисел також число натуральне. А ось різниця двох натуральних чисел не завжди є числом натуральним, наприклад  .
. . На множині
. На множині  вже можна здійснювати і операцію віднімання, тобто
вже можна здійснювати і операцію віднімання, тобто 
 .
. .
. .
. , де
, де  .
. , то число
, то число  і задовольняє нерівність:
і задовольняє нерівність: 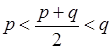 .
. прямокутного трикутника, обидва катети якого дорівнюють 1. Згідно з теоремою того ж Піфагора, легко знаходимо, що
прямокутного трикутника, обидва катети якого дорівнюють 1. Згідно з теоремою того ж Піфагора, легко знаходимо, що 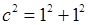 , отже у сучасному запису
, отже у сучасному запису  . Чи є це число раціональним? Припустимо, що це так, тоді
. Чи є це число раціональним? Припустимо, що це так, тоді  (не обмежуючи загальності, ці числа можна вважати натуральними, а не просто цілими, оскільки
(не обмежуючи загальності, ці числа можна вважати натуральними, а не просто цілими, оскільки  ) такі, що
) такі, що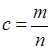 .
. – нескоротний, оскільки, якщо це не так, то ми його скоротимо настільки, наскільки це можливо, і зробимо з нього нескоротний.
– нескоротний, оскільки, якщо це не так, то ми його скоротимо настільки, наскільки це можливо, і зробимо з нього нескоротний. , то
, то  , а це означає, що
, а це означає, що  – число парне. Тоді і
– число парне. Тоді і 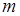 – парне. Дійсно, якщо це не так, то
– парне. Дійсно, якщо це не так, то  , і тоді
, і тоді  – непарне, що суперечить встановленому. Отже
– непарне, що суперечить встановленому. Отже  , і тоді
, і тоді  , звідки
, звідки  , тобто
, тобто  – парне, а тоді, аналогічно попередньому, і
– парне, а тоді, аналогічно попередньому, і 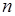 – число парне. А якщо
– число парне. А якщо 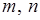 – парні, то дріб
– парні, то дріб  (доведіть самостійно),
(доведіть самостійно),  , славнозвісне число
, славнозвісне число  та інші.
та інші. .
.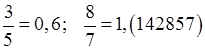 .
. ,
,  .
. .
. -му знаку після коми, отримаємо раціональне число:
-му знаку після коми, отримаємо раціональне число: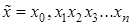 .
. . Тоді
. Тоді .
. , тобто
, тобто .
.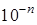 .
. – довільне раціональне число. Тоді
– довільне раціональне число. Тоді 
 .
.
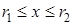 , причому
, причому  .
.
 відповідає одна і тільки одна точка числової осі, і навпаки, кожній точці числової осі відповідає одне і тільки одне дійсне число (рис. 6).
відповідає одна і тільки одна точка числової осі, і навпаки, кожній точці числової осі відповідає одне і тільки одне дійсне число (рис. 6).


 і
і  – дійсні числа, причому
– дійсні числа, причому  .
. числової осі називається множина точок
числової осі називається множина точок  .
. числової осі називається множина точок
числової осі називається множина точок  .
. чи
чи 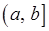 числової осі називається множина точок
числової осі називається множина точок  чи
чи  .
. відрізку належать, а інтервалу не належать. В півінтервалі одна з цих точок йому належить, а інша ні.
відрізку належать, а інтервалу не належать. В півінтервалі одна з цих точок йому належить, а інша ні. .
. – довільне дійсне число. Околом точки
– довільне дійсне число. Околом точки  , який містить точку
, який містить точку  .
. є околами точки
є околами точки  . Зауважимо, що точка
. Зауважимо, що точка 


 .
. –околом точки
–околом точки  .
.


 , яке визначається за формулою:
, яке визначається за формулою:
 .
.
 виконано:
виконано: .
. тоді і тільки тоді, коли
тоді і тільки тоді, коли  .
. .
. .
.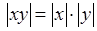 .
.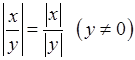 .
. .
. .
. – дві точки числової осі. Відстань між ними, очевидно, дорівнює
– дві точки числової осі. Відстань між ними, очевидно, дорівнює  (рис. 10).
(рис. 10).


 . Справедливо і зворотне, тобто якщо виконано
. Справедливо і зворотне, тобто якщо виконано  . Зокрема, якщо
. Зокрема, якщо  , де
, де  і навпаки.
і навпаки. . Тоді отримаємо так званий окіл з виколотою точкою
. Тоді отримаємо так званий окіл з виколотою точкою  .
. називається найбільше ціле, яке не більше, ніж
називається найбільше ціле, яке не більше, ніж  або
або  . Наприклад:
. Наприклад: .
. .
.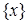 . Таким чином:
. Таким чином: .
.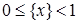 . Наприклад:
. Наприклад:  .
. :
: ;
; ;
; ;
; .
. :
: ;
; ;
; ;
; .
. :
:  .
.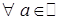 визначено одне з співвідношень:
визначено одне з співвідношень: 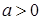 ,
,  ,
,  ; при
; при 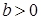 виконано:
виконано:  ;
;  , якщо
, якщо  ;
;  , якщо
, якщо 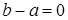 .
. таких, що
таких, що 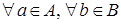 виконано
виконано  , існує таке число
, існує таке число  , що
, що  .
. називається обмеженою зверху, якщо
називається обмеженою зверху, якщо  таке, що
таке, що  :
:  .
. таке, що
таке, що  .
. при цьому називається верхньою гранню множини
при цьому називається верхньою гранню множини  – нижньою гранню множини
– нижньою гранню множини  . Тобто у якості числа
. Тобто у якості числа 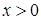 . У якості числа
. У якості числа  . Найбільша з нижніх граней множини
. Найбільша з нижніх граней множини 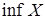 .
. , то виконано умови:
, то виконано умови: ;
; .
. , то виконано умови:
, то виконано умови: ;
; .
. , то
, то  . А якщо
. А якщо  , то
, то  .
.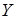 – множину всіх верхніх граней множини
– множину всіх верхніх граней множини  виконано:
виконано:  . Внаслідок аксіоми неперервності (див. п. 3) існує таке число
. Внаслідок аксіоми неперервності (див. п. 3) існує таке число  , що
, що 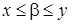 . Отже число
. Отже число  виконано
виконано  , то
, то  . Аналогічно доводиться існування точної нижньої грані.
. Аналогічно доводиться існування точної нижньої грані.


