
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деякі методи обчислення границь функцій.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Використання апарату нескінченно малих дозволяє досить ефективно обчислювати границі функцій. В простіших випадках границю функції у точці можна знайти на підставі теорем про границю суми, різниці, добутку і частки функцій. Відповідний приклад ми розглянули у п. 20. Вивчення більш складних випадків почнемо з границі відношення двох функцій:
Якщо існують Підведемо підсумок у вигляді наступної таблиці:
В ній проставлено значення Бувають невизначеності інших типів. Найбільш часто зустрічаються наступні. 1. 2. 3. 4. 5. 6. В багатьох випадках ці невизначеності можна звести до невизначеностей типу
I. Невизначеність типу Розглянемо границю вигляду:
Якщо хоча б один з поліномів Перейдемо до прикладів. а) Тут чисельник і знаменник при
б) Тут також має місце невизначеність типу
в) Очевидно, що при
II. Невизначеність типу У таких ситуаціях намагаються тим чи іншим чином позбутися ірраціональностей у чисельнику чи у знаменнику. а) Помножимо чисельник і знаменник на
б) Помножимо чисельник і знаменник на добуток
Іноді від ірраціональності можна позбавитись введенням нової змінної. в) Введемо заміну
III. Невизначеність типу У таких ситуаціях ділять чисельник і знаменник на а) Маємо невизначеність типу
Застосовуючи цей метод, легко отримати наступний результат. Якщо
IY. Невизначеність типу Тут можна також застосовувати метод ділення на а) Поділимо чисельник і знаменник на
б) Тут найвища степінь змінної
Y. Невизначеність типу Такого типу невизначеності одночасним множенням і діленням на деякий вираз намагаються звести до невизначеностей типу
Помножимо і поділимо на
Отримали невизначеність
YI. Використання еквівалентних нескінченно малих. Нехай треба обчислити
Аналогічно:
Таким чином, якщо нескінченно мала міститься під знаком границі у якості множника, або дільника, то її можна замінити на їй еквівалентну. Зокрема, якщо
Зауваження. Суттєво, що нескінченно мала повинна міститись у якості множника або дільника. Якщо вона міститься у якості доданку, то, взагалі кажучи, її не можна замінити на еквівалентну. Наприклад, було б помилкою наступне міркування:
Перейдемо до прикладів. а) Невизначеність типу
б) Невизначеність
Тут замінили:
в) Невизначеність типу
А тут вже можна замінити
Використовуючи першу важливу границю (25.1), знайдемо площу круга радіуса
Площа кожного трикутника, на які розбито многокутник, дорівнює:
YII. Використання другої важливої границі. Ця границя використовується для розкриття невизначеностей типу
Таким чином задача звелася до обчислення границі Перейдемо до прикладів. а)
б)
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 829; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.48 (0.007 с.) |

 .
. ,
,  ,
,  то границя дорівнює
то границя дорівнює  . Але границі як чисельника, так і знаменника можуть дорівнювати нулю, а також можуть бути нескінченними. Нехай, наприклад,
. Але границі як чисельника, так і знаменника можуть дорівнювати нулю, а також можуть бути нескінченними. Нехай, наприклад,  . Тоді границя відношення буде нескінченною, оскільки функція, яка прямує до скінченої відмінної від нуля границі, ділиться на нескінченно малу. Нескінченність вийде і тоді, коли
. Тоді границя відношення буде нескінченною, оскільки функція, яка прямує до скінченої відмінної від нуля границі, ділиться на нескінченно малу. Нескінченність вийде і тоді, коли  . Якщо
. Якщо  ,
,  , то границя відношення, очевидно, буде дорівнювати нулю.
, то границя відношення, очевидно, буде дорівнювати нулю.
 в залежності від
в залежності від  та
та  . Ми бачимо, що це значення можна однозначно визначити в усіх випадках, крім двох: а саме, коли границі обох функцій водночас дорівнюють нулю, або водночас дорівнюють нескінченності. Такі ситуації називаються невизначеностями. В даному випадку ми маємо справу з невизначеностями типу
. Ми бачимо, що це значення можна однозначно визначити в усіх випадках, крім двох: а саме, коли границі обох функцій водночас дорівнюють нулю, або водночас дорівнюють нескінченності. Такі ситуації називаються невизначеностями. В даному випадку ми маємо справу з невизначеностями типу  та
та  . Границя виразів такого роду може бути і нулем, і скінченим, відмінним від нуля числом, і нескінченністю, і навіть взагалі може не існувати. Якщо вдається встановити, яка саме з цих ситуацій має місце, то кажуть, що невизначеність розкрита.
. Границя виразів такого роду може бути і нулем, і скінченим, відмінним від нуля числом, і нескінченністю, і навіть взагалі може не існувати. Якщо вдається встановити, яка саме з цих ситуацій має місце, то кажуть, що невизначеність розкрита. , коли
, коли  ,
,  . Це невизначеність типу
. Це невизначеність типу  .
. , коли
, коли  ,
,  .
. , коли
, коли  ,
,  .
. . Це невизначеність типу
. Це невизначеність типу  .
. .
. .
. в раціональних виразах.
в раціональних виразах. , де
, де  – поліном степеня
– поліном степеня 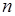 , а
, а  – поліном степеня
– поліном степеня 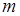 , причому
, причому  , тобто
, тобто  є коренем обох поліномів. Тоді мають місце співвідношення:
є коренем обох поліномів. Тоді мають місце співвідношення: , де
, де  – поліном степеня
– поліном степеня 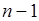 , а
, а  – поліном степеня
– поліном степеня  . Підставляючи ці вирази до функції, що стоїть під знаком границі, і, скорочуючи на
. Підставляючи ці вирази до функції, що стоїть під знаком границі, і, скорочуючи на  , отримаємо:
, отримаємо: .
. , то треба ще раз повторити описаний прийом.
, то треба ще раз повторити описаний прийом. .
. прямують до нуля, отже маємо невизначеність типу
прямують до нуля, отже маємо невизначеність типу  .
.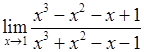 .
. (зокрема, за схемою Горнера), або групуванням доданків у чисельнику і знаменнику.
(зокрема, за схемою Горнера), або групуванням доданків у чисельнику і знаменнику.
 .
. .
. чисельник і знаменник прямують до нуля, отже маємо невизначеність типу
чисельник і знаменник прямують до нуля, отже маємо невизначеність типу  .
. .
. .
.
 .
. .
. . Отримаємо:
. Отримаємо:

 .
. .
.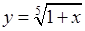 . Тоді
. Тоді  при
при  . Маємо:
. Маємо:
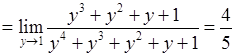 .
. в раціональних виразах.
в раціональних виразах. , де
, де  – найвища степінь змінної
– найвища степінь змінної  з тих, в яких вона міститься у чисельнику та у знаменнику.
з тих, в яких вона міститься у чисельнику та у знаменнику. .
. .
. , оскільки вирази вигляду
, оскільки вирази вигляду  прямують до нуля при
прямують до нуля при  .
. , то
, то
 .
. , а під кубічним – на
, а під кубічним – на  . Отримаємо:
. Отримаємо: .
. .
. . Отже поділимо чисельник і знаменник на
. Отже поділимо чисельник і знаменник на  .
.
 , оскільки вираз у чисельнику прямує до 1 при
, оскільки вираз у чисельнику прямує до 1 при  . Розглянемо приклад.
. Розглянемо приклад. .
. . Отримаємо:
. Отримаємо:
 .
. .
. , і нехай функція
, і нехай функція  є нескінченно малою при
є нескінченно малою при  . Припустимо, що при
. Припустимо, що при  . Тоді
. Тоді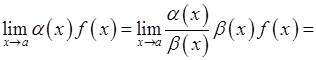
 .
. .
. , і при
, і при  ,
,  , то
, то .
. (на підставі того, що
(на підставі того, що  при
при  .
.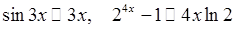 . Отримаємо:
. Отримаємо: .
. .
. . Тоді отримаємо:
. Тоді отримаємо: .
. .
. .
. ,
,  , оскільки тут
, оскільки тут  . Тому зробимо заміну змінної:
. Тому зробимо заміну змінної:  ;
;  :
: .
. , оскільки
, оскільки  . Тоді
. Тоді .
. як границю площ вписаних правильних многокутників, які розбито на рівні трикутники, тобто розв’яжемо задачу сформульовану в п.8 (рис.14). На підставі означення границі функції за Гейне з рівності (25.1) випливає, що для будь якої послідовності
як границю площ вписаних правильних многокутників, які розбито на рівні трикутники, тобто розв’яжемо задачу сформульовану в п.8 (рис.14). На підставі означення границі функції за Гейне з рівності (25.1) випливає, що для будь якої послідовності  такої, що
такої, що  , і
, і  , виконано:
, виконано: .
. , де
, де  , тобто отримали відому формулу площі круга.
, тобто отримали відому формулу площі круга. – нескінченно малі при
– нескінченно малі при 
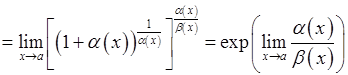 .
.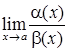 .
.
 .
.

 .
.


