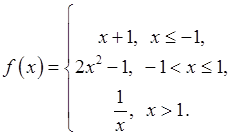Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розривні функції. Класифікація точок розриву функції.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Якщо у деякій точці Означення. Кажуть, що у точці Графіки таких функцій зображені на рис. 39, 40 (б). Такого типу розриви має, наприклад, функція
Рис. 49.
Ця функція має розриви I роду у точках Означення. Кажуть, що у точці Графік такої функції показано на рис. 40(в). Прикладом може бути функція
Рис. 50. Означення. Кажуть, що в точці Графік такої функції показано на рис. 40(г). Характерною його ознакою є наявність «виколотої» точки. Наприклад, функція Якщо функція
Така функція вже буде неперервною у точці
Контрольні питання. 1. Що розуміється під поняттям множини? 2. Що таке об’єднання та перетин множин? 3. Що таке числові множини? Які основні числові множини ви знаєте? 4. Що таке раціональне число? Що таке дійсне число? 5. Які множини називаються зліченними? Чи є зліченною множина раціо- нальних чисел? Множина дійсних чисел? 6. Що таке інтервал на числовій прямій? Що таке відрізок або сегмент? 7. Що таке числова послідовність? Які існують способи задання послідов- ності? 8. Які послідовності називаються обмеженими? 9. Які послідовності називаються монотонними? 10. Що таке границя послідовності? Яка послідовність називається збіжною? 11. Чи випливає з обмеженості послідовності її збіжність? Наведіть відповід- ні приклади? 12. Яка послідовність називається нескінченно малою? Чи можна стверджу- вати, що частка двох нескінченно малих послідовностей також є нескін- ченно малою? Наведіть відповідні приклади. Чи можна стверджувати, що різниця двох нескінченно малих послідовностей є також нескінченно ма- лою? 13. Яка послідовність називається нескінченно великою? Чи можна стверд- жувати, що частка двох нескінченно великих послідовностей є також не- скінченно великою? Чи можна стверджувати, що різниця двох нескінчен- но великих послідовностей є також нескінченно великою? Наведіть відпо- відні приклади. 14. Дайте означення функції. Які існують способи задання функції? 15. Що таке суперпозиція функцій? Що таке складена функція? 16. Що називається функцією, оберненої до даної функції? Який зв’язок між графіками двох взаємно обернених функцій? 17. Які функції називаються елементарними? Наведіть приклади елементар- них та неелементарних функцій? Чи можна стверджувати, що сума двох елементарних функцій є також функцією елементарною? Чи можна стверджувати, що сума двох неелементарних функцій є також функцією неелементарною? Наведіть відповідні приклади. 18. Дайте означення границі функції в точці та у нескінченності за Коші та за Гейне. 19. Що таке однобічні границі функції? 20. Яка функція називається неперервною в точці? Яка функція називається розривною в точці? Які існують типи розривів функції?
Вправи для самостійного розв’язування.
Вправи до розділу 5. 1. Методом математичної індукції довести справедливість рівностей: 1) 3) 2. Написати п”ять перших членів послідовностей з наступними загальними членами: 1) 4) 3. На підставі декількох перших членів послідовностей встановити формулу їх загальних членів: 1) 3) 5) 4. Використовуючи мову « 1) 5. Довести, що послідовність 6. Знайти границі 1) 4) 7) 9) 11) 14) 17) 19) 7. Знайти область визначення функцій 1) 4) 7) 10) 8. Дослідити функції на парність, непарність і періодичність. 1) 4) 7) 9. Побудувати графіки функцій: 1) 4) 7) 10) 13) 16) 19)
10. Сформулювати за допомогою нерівностей, що означає: 1) 4) 7) 10) 13) 16) 11. Сформулювати за допомогою нерівностей, що означає: 1) 4) 7) 10)
1) 13. Знайти границі: 1) 14. Знайти границі шляхом розкладання чисельника і знаменника на множники: 1) 4) 15. Знайти границі шляхом одночасного множення чисельника і знаменника на вираз, спряжений чисельнику, або знаменнику: 1) 3) 16. Знайти границі шляхом ділення чисельника і знаменника на 1) 4) 17. Знайти границі шляхом одночасного множення і ділення на спряжений вираз: 1) 3) 5) 18. Знайти границі, використовуючи еквівалентні нескінченно малі: 1) 4) 19. Знайти границі, використовуючи другу важливу границю: 1) 4) 20. Задано функцію:
Чи буде ця функція неперервною? Побудувати її графік. 21. Знайти числа
22. Показати, що наступні функції не являються неперервними у точці 1) 23. Дослідити функцію на неперервність і побудувати схематично її графік: 1) 4)
[1] Больцано Бернард (1781–1848) – чеський математик. Вейєрштрасс Карл (1815–1897) – видатний німецький математик. [2] Коші Огюстен Луї (1789–1857) – видатний французький математик. * Гейне Генріх Едуард (1821–1881) – німецький математик. Не путати з відомим поетом Генріхом Гейне.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 порушується хоч би одна з умов, наведених в означенні неперервності функції в точці, то кажуть. що у точці
порушується хоч би одна з умов, наведених в означенні неперервності функції в точці, то кажуть. що у точці  має розрив I роду, якщо в цій точці існують скінченні однобічні границі, і не всі числа
має розрив I роду, якщо в цій точці існують скінченні однобічні границі, і не всі числа 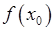 (у випадку визначеності функції в точці
(у випадку визначеності функції в точці 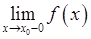 ,
, 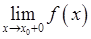 співпадають.
співпадають.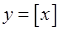 (ціла частина
(ціла частина  ), графік якої зображено на рис. 49.
), графік якої зображено на рис. 49.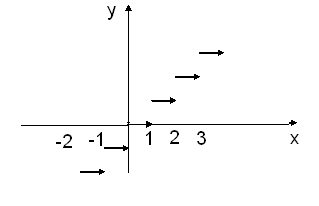
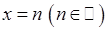 .
.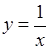 (розрив II роду у точці
(розрив II роду у точці  ), функція
), функція  (розриви II роду у точках
(розриви II роду у точках 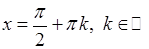 ). Розрив II роду має у точці
). Розрив II роду має у точці 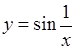 , оскільки не існує границі цієї функції при
, оскільки не існує границі цієї функції при 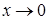 (рис. 50).
(рис. 50).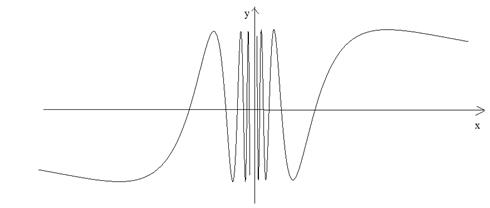
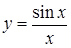 має усувний розрив в точці
має усувний розрив в точці 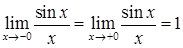 , але функція не визначена у цій точці.
, але функція не визначена у цій точці.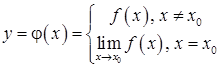
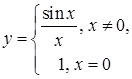 неперервна у будь якій точці числової прямої, у тому числі у точці
неперервна у будь якій точці числової прямої, у тому числі у точці 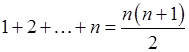 , 2)
, 2) 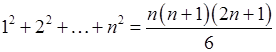 ,
,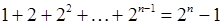 , 4)
, 4) 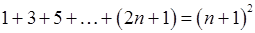 .
.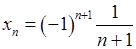 , 2)
, 2) 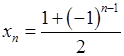 , 3)
, 3) 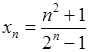 ,
,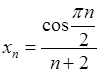 , 5)
, 5) 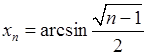 , 6)
, 6) 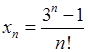 .
.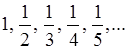 2)
2) 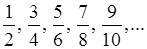
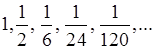 4)
4) 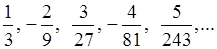
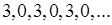 6)
6) 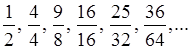
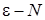 », довести наступні рівності:
», довести наступні рівності: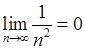 , 2)
, 2) 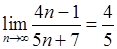 , 3)
, 3) 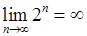 .
.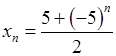 не має ніякої границі.
не має ніякої границі.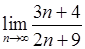 , 2)
, 2) 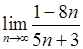 , 3)
, 3) 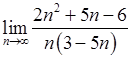 ,
,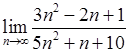 . 5)
. 5) 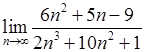 , 6)
, 6) 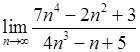 ,
,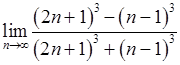 , 8)
, 8) 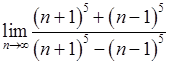
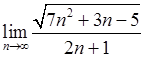 , 10)
, 10) 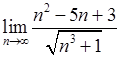 ,
,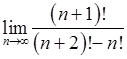 , 12)
, 12) 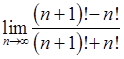 , 13)
, 13) 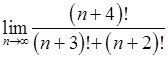 ,
,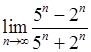 , 15)
, 15) 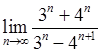 , 16)
, 16) 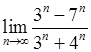 ,
,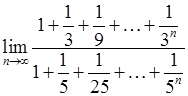 , 18)
, 18) 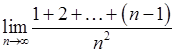 ,
,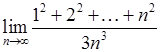 , 20)
, 20) 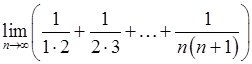 .
.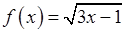 , 2)
, 2) 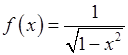 , 3)
, 3) 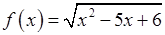 ,
,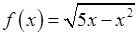 , 5)
, 5) 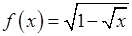 , 6)
, 6) 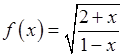 ,
,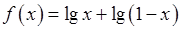 , 8)
, 8) 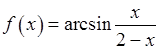 , 9)
, 9) 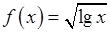 ,
,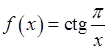 , 11)
, 11) 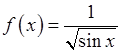 , 12)
, 12) 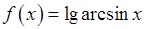 .
.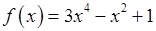 , 2)
, 2) 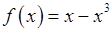 , 3)
, 3) 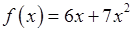 ,
,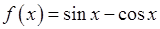 , 5)
, 5) 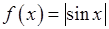 6)
6) 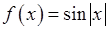 ,
,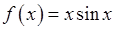 , 8)
, 8) 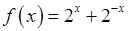 , 9)
, 9) 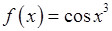 .
.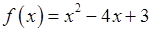 , 2)
, 2) 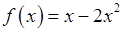 , 3)
, 3) 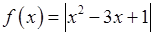 ,
,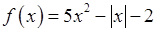 , 5)
, 5) 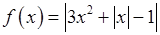 , 6)
, 6) 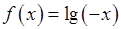 ,
,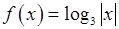 , 8)
, 8) 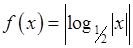 , 9)
, 9) 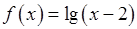 ,
,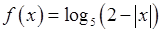 , 11)
, 11) 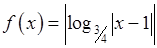 , 12)
, 12) 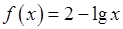 ,
,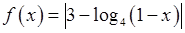 , 14)
, 14) 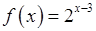 , 15)
, 15) 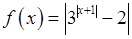 ,
,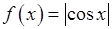 , 18)
, 18) 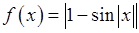 ,
,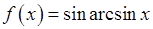 , 20)
, 20) 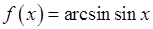 ,
,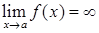 , 2)
, 2) 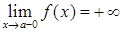 , 3)
, 3) 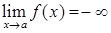 ,
,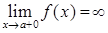 , 5)
, 5) 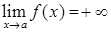 , 6)
, 6) 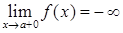 ,
,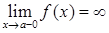 , 8)
, 8) 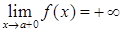 ,
,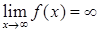 , 11)
, 11) 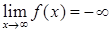 , 12)
, 12) 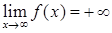 ,
,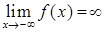 , 14)
, 14) 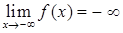 , 15)
, 15) 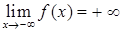 ,
,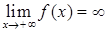 , 17)
, 17) 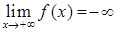 , 18)
, 18) 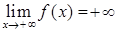 .
.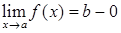 , 2)
, 2) 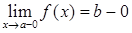 , 3)
, 3) 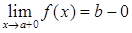 ,
,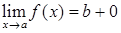 , 5)
, 5) 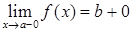 , 6)
, 6) 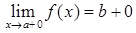 ,
,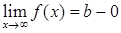 , 8)
, 8) 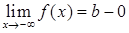 , 9)
, 9) 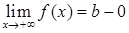 ,
,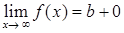 , 11)
, 11) 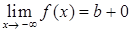 , 12)
, 12) 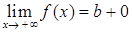 .
. », довести наступні рівності:
», довести наступні рівності:
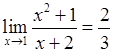 , 2)
, 2) 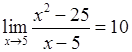 , 3)
, 3) 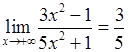 .
.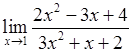 , 2)
, 2) 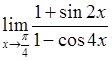 , 3)
, 3) 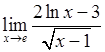 .
.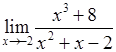 , 2)
, 2) 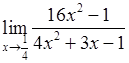 3)
3) 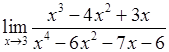 ,
,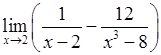 , 5)
, 5) 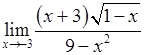 , 6)
, 6) 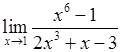 .
.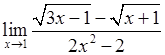 , 2)
, 2) 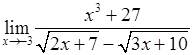 ,
,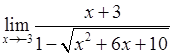 , 4)
, 4) 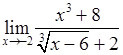 5)
5) 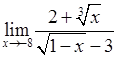 .
.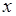 у найстаршій степені з тих, в яких він міститься у чисельнику та знаменнику:
у найстаршій степені з тих, в яких він міститься у чисельнику та знаменнику: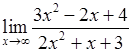 , 2)
, 2) 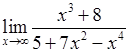 , 3)
, 3) 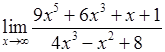 ,
,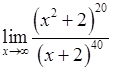 , 5)
, 5) 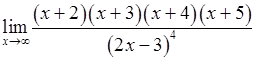 ,
,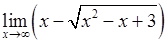 , 2)
, 2) 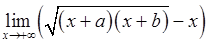 ,
,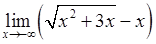 , 4)
, 4) 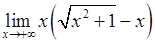 ,
,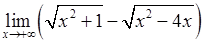 , 6)
, 6) 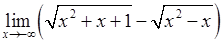 .
.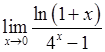 , 2)
, 2) 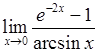 , 3)
, 3) 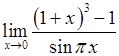 ,
,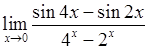 , 5)
, 5) 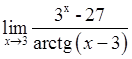 , 6)
, 6) 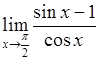 .
.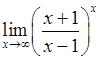 , 2)
, 2) 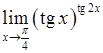 , 3)
, 3) 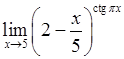 ,
,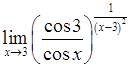 , 5)
, 5) 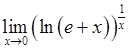 , 6)
, 6) 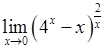 .
.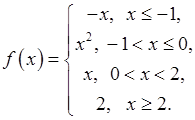
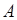 і
і 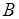 такі, щоб функція
такі, щоб функція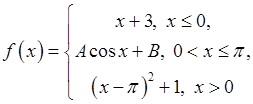 була неперервною. Побудувати її графік.
була неперервною. Побудувати її графік.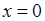 . Довизначити кожну з них у цій точці так, щоб вона в цій точці стала неперервною:
. Довизначити кожну з них у цій точці так, щоб вона в цій точці стала неперервною: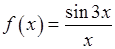 , 2)
, 2) 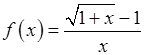 , 3)
, 3) 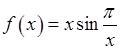 .
.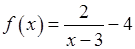 , 2)
, 2) 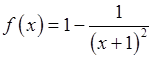 , 3)
, 3) 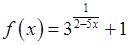 ,
,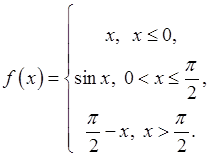 , 5)
, 5)