
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нескінченно малі та нескінченно великі послідовності.Содержание книги
Поиск на нашем сайте
Означення. Послідовність Тобто якщо Наприклад, послідовності Теорема. Сума та різниця двох нескінченно малих послідовностей є нескінченно малою послідовністю. Доведення. Нехай
Це й означає, що послідовності Доведена властивість легко поширюється на будь яке скінченне число доданків. Теорема. Добуток нескінченно малої послідовності на обмежену послідовність (зокрема, сталу) є нескінченно малою послідовністю. Доведення. Нехай послідовність
Це й означає, що послідовність Наслідок. Добуток двох нескінченно малих послідовностей є нескінченно малою послідовністю. Дійсно, нехай Ця властивість легко поширюється на будь яке скінченне число множників. Зауваження. Про частку двох нескінченно малих послідовностей у загальному випадку нічого сказати не можна. Така частка може бути нескінченно малою, а може й не бути. І взагалі навіть може не бути збіжною. Приклади. 1. Нехай 2. Нехай 3. Нехай Теорема. Для виконання рівності Доведення. Необхідність. Нехай Достатність. Нехай Приклад. Нехай
Теорема (арифметичні властивості границь послідовностей). Нехай 1) 2) 3) якщо Доведення. Оскільки
Оскільки З цієї властивості і того, що
Тобто сталий множник можна виносити за знак границі. Доведемо тепер, що послідовність
Оскільки Покажемо, що послідовність
Покладемо Означення. Послідовність Може скластися враження, що поняття нескінченно великої послідовності та поняття необмеженої послідовності співпадають. Насправді це не так. Нескінченно велика послідовність дійсно є необмеженою. Але обернене твердження невірне. Розглянемо таку послідовність:
Ця послідовність необмежена, але не є нескінченно великою. Дійсно, якби вона була нескінченно великою, то Теорема. Якщо послідовності Доведення. Оскільки Аналогічно доводиться, що якщо Зауваження. Про послідовність Приклади. 1. Нехай 2. Нехай 3. Нехай 4. Нехай Теорема. Якщо послідовності Доведення. Оскільки послідовність Зауваження. Про частку двох нескінченно великих послідовностей у загальному випадку нічого сказати не можна, також як про частку двох нескінченно малих. Відповідні приклади пропонується навести самостійно. Теорема. Сума нескінченно великої та обмеженої (зокрема, сталої) послідовностей є послідовність нескінченно велика. Доведення. Нехай послідовність Теорема. Добуток нескінченно великої послідовності на сталу є послідовністю нескінченно великою. Доведення. Нехай Зауваження. Про добуток обмеженої послідовності на нескінченно велику та нескінченно малої на нескінченно велику у загальному випадку нічого сказати не можна (відповідні приклади наведіть самостійно). Теорема. Якщо Доведення. Нехай послідовність
Навпаки, нехай послідовність
Теорему доведено.
12. Границя монотонної послідовності. Число
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 2365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.241 (0.008 с.) |

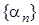 називається нескінченно малою, якщо
називається нескінченно малою, якщо 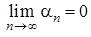 .
.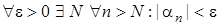 .
.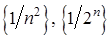 є нескінченно малими (див. п. 9, приклад 2 та п. 10, приклад 1).
є нескінченно малими (див. п. 9, приклад 2 та п. 10, приклад 1). – нескінченно малі послідовності. Тоді
– нескінченно малі послідовності. Тоді 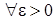
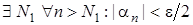 та
та 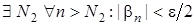 . Позначимо
. Позначимо 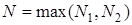 . Тоді при
. Тоді при 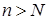 водночас буде виконано
водночас буде виконано 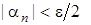 ,
, 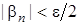 . Отже
. Отже .
. нескінченно малі.
нескінченно малі.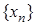 – обмежена. Тоді
– обмежена. Тоді 
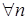 :
: 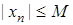 . Нехай послідовність
. Нехай послідовність 
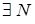
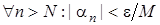 . Тоді
. Тоді 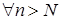 буде виконано:
буде виконано: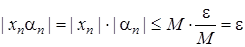 .
.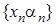 – нескінченно мала.
– нескінченно мала.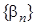 є обмеженою, оскільки вона збіжна, а тоді послідовність
є обмеженою, оскільки вона збіжна, а тоді послідовність 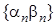 – нескінченно мала.
– нескінченно мала.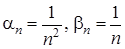 . Ці послідовності нескінченно малі. Частка
. Ці послідовності нескінченно малі. Частка 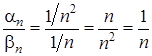 у даному випадку також нескінченно мала.
у даному випадку також нескінченно мала.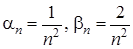 . Ці послідовності нескінченно малі. Але частка
. Ці послідовності нескінченно малі. Але частка 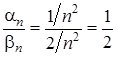 не є нескінченно малою, її границя дорівнює
не є нескінченно малою, її границя дорівнює 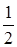 .
.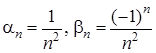 . Ці послідовності нескінченно малі. Але частка
. Ці послідовності нескінченно малі. Але частка 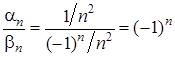 взагалі не є збіжною послідовністю (див. п. 9, приклад 4).
взагалі не є збіжною послідовністю (див. п. 9, приклад 4).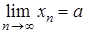 необхідно і достатньо виконання рівності
необхідно і достатньо виконання рівності 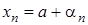 , де
, де 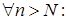
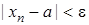 . Покладемо
. Покладемо 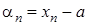 . Тоді послідовність
. Тоді послідовність 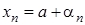 .
.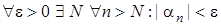 . Оскільки
. Оскільки  . Легко встановлюємо, що
. Легко встановлюємо, що 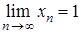 . Маємо:
. Маємо: , де
, де  – нескінченно мала.
– нескінченно мала.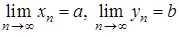 . Тоді:
. Тоді: ;
;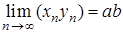 ;
; , то
, то 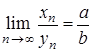 .
.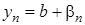 , де
, де 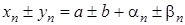 . Оскільки послідовність
. Оскільки послідовність  .
. також є нескінченно малими, звідки випливає, що й послідовність
також є нескінченно малими, звідки випливає, що й послідовність 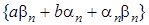 – нескінченно мала, і на підставі попередньої теореми
– нескінченно мала, і на підставі попередньої теореми 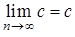 , зокрема, випливає, що
, зокрема, випливає, що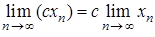 .
.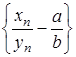 – нескінченно мала. Дійсно:
– нескінченно мала. Дійсно: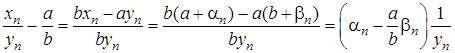 .
. також нескінченно мала.
також нескінченно мала. обмежена. Оскільки
обмежена. Оскільки  , то
, то 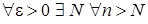 :
: 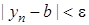 . Тоді
. Тоді 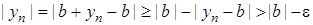 .
.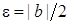 . Тоді
. Тоді 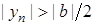 , і отже
, і отже 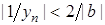 . Тобто послідовність
. Тобто послідовність  – нескінченно мала як добуток нескінченно малої послідовності на обмежену. Таким чином послідовність
– нескінченно мала як добуток нескінченно малої послідовності на обмежену. Таким чином послідовність 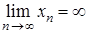 .
.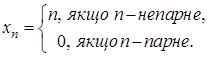
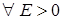
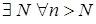 :
:  . Але якщо
. Але якщо 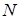 – непарне, то
– непарне, то 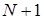 – парне, і тоді
– парне, і тоді 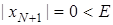 . А якщо
. А якщо 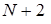 також парне, і тоді
також парне, і тоді 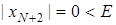 . У будь якому разі потрібна умова не виконується.
. У будь якому разі потрібна умова не виконується. нескінченно великі, причому
нескінченно великі, причому 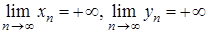 , то послідовність
, то послідовність  також нескінченно велика, і
також нескінченно велика, і  .
.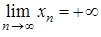 , то
, то 
 . Оскільки
. Оскільки 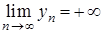 , то
, то 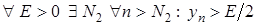 . Покладемо
. Покладемо 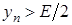 . Отже
. Отже  , тобто
, тобто  , то
, то 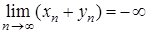 . Тобто сума двох нескінченно великих послідовностей одного знаку є також нескінченно великою послідовністю того ж знаку.
. Тобто сума двох нескінченно великих послідовностей одного знаку є також нескінченно великою послідовністю того ж знаку.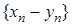 (також як і про суму нескінченно великих послідовностей різних знаків) у загальному випадку нічого сказати не можна – ця послідовність може бути нескінченно великою, а може й не бути, і може навіть взагалі не мати ніякої границі (ані скінченної, ані нескінченної).
(також як і про суму нескінченно великих послідовностей різних знаків) у загальному випадку нічого сказати не можна – ця послідовність може бути нескінченно великою, а може й не бути, і може навіть взагалі не мати ніякої границі (ані скінченної, ані нескінченної).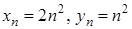 . Ці послідовності нескінченно великі. В даному випадку послідовність
. Ці послідовності нескінченно великі. В даному випадку послідовність  – також нескінченно велика.
– також нескінченно велика.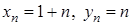 . Ці послідовності нескінченно великі. Але послідовність
. Ці послідовності нескінченно великі. Але послідовність 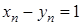 не є нескінченно великою:
не є нескінченно великою:  .
.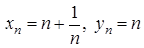 . Ці послідовності нескінченно великі. Але послідовність
. Ці послідовності нескінченно великі. Але послідовність 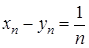 не є нескінченно великою, вона навіть нескінченно мала.
не є нескінченно великою, вона навіть нескінченно мала.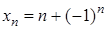 ,
, 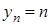 . Ці послідовності нескінченно великі. Але послідовність
. Ці послідовності нескінченно великі. Але послідовність 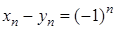 взагалі не має ніякої границі.
взагалі не має ніякої границі. – нескінченно велика.
– нескінченно велика.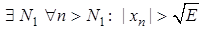 . Оскільки послідовність
. Оскільки послідовність 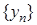 – нескінченно велика, то
– нескінченно велика, то  . Покладемо:
. Покладемо: 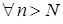 водночас виконано:
водночас виконано: 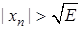 ,
, 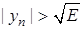 . Отже
. Отже  , а це й означає, що
, а це й означає, що 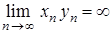 , тобто послідовність
, тобто послідовність 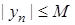 . І
. І 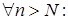
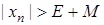 . Тоді
. Тоді 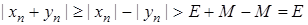 , тобто послідовність
, тобто послідовність  , а
, а 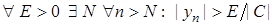 . Отже
. Отже 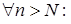

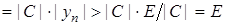 , тобто
, тобто  виконано
виконано 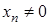 , то послідовність
, то послідовність 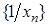 – нескінченно мала послідовність.
– нескінченно мала послідовність.
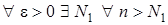 виконано
виконано 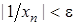 . Задамо довільне
. Задамо довільне  і покладемо
і покладемо 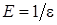 . Для цього
. Для цього 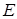 знайдеться номер
знайдеться номер 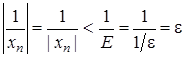 , а це й означає, що послідовність
, а це й означає, що послідовність 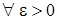
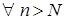 виконано
виконано 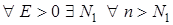 виконано:
виконано: 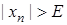 . Задамо довільне
. Задамо довільне 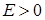 і покладемо
і покладемо 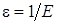 . Для цього
. Для цього 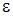 знайдеться номер
знайдеться номер  , а це й означає, що послідовність
, а це й означає, що послідовність 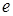 .
.


