
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неперервність функції в точці.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо графіки декількох функцій.
Рис. 40.
Яка ознака поєднує графіки, зображені на рис. 40 (б,в,г), на відміну від графіка, зображеного на рис. 40(а)? Ми можемо сказати, що графік на рис. 40(а) є суцільною лінією, в той час, як графіки на рис. 40 (б,в,г) суцільними лініями не є. Іншими словами, графік на рис. 40(а) можна провести, не видриваючи олівця від паперу, а з графіками рис. 40(б,в,г) це зробити неможливо. Якщо розглянути точку Такі властивості функцій відображають відповідні властивості процесів, які цими функціями описуються. Розглянемо приклади. 1. Залежність атмосферного тиску
Рис. 41.
Бачимо, що це суцільна лінія, тобто графік типу 40(а). 2. Відомо, що залежність електричного опору металів Схематична залежність електричного опору металів від температури показана на рис. 42.
Рис. 42.
3. Залежність густини ідеального газу від температури
Рис. 43.
Тобто маємо графік типу 40(в). Існують також процеси типу 40(г). Все це свідчить про те, що ми повинні вміти встановлювати подібні властивості функцій і не лише у тих випадках, коли є графічні їх зображення, а й тоді, коли функції задаються аналітичним способом. Але це можливо тільки тоді, коли ми маємо чіткі математичні означення всіх цих ситуацій. Отже саме до них ми тепер і переходимо.
Означення. Функція 1) функція визначена в деякому околі точки 2) існує 3) Якщо використати означення границі функції у точці на мові « Функція Зверніть увагу: у означенні границі функції у точці суттєвою особливістю, як ми відмічали, була умова, що Враховуючи, що
Тобто знаки границі і неперервної функції можна змінювати місцями. Можна дати інше означення неперервності функції у точці. Позначимо як
Рис. 44.
Тепер, оскільки
Таким чином, функція називається неперервною у точці Геометрично факт неперервності функції у точці Приклади. 1. Довести, що функція Візьмемо довільне
Величина
2. Довести, що функція
неперервна у точці Функція визначена на
3. Довести, що функція
Надамо значенню аргументу
Функції, неперервні в точці, мають деякі прості властивості, які являються наслідками відповідних властивостей границь функцій (див. п. 20). Властивість 1. Якщо функція Властивість 2. Якщо функція Властивість 3. Якщо функції Властивість 4 (неперервність складеної функції). Нехай функція Доведення. Надамо значенню
За аналогією з однобічними границями функції вводиться поняття однобічної неперервності функції в точці. Означення. Функція
|
||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.214.156 (0.012 с.) |



 на цих графіках, то помітимо, що функція
на цих графіках, то помітимо, що функція  визначена у цій точці, і, якщо змінити значення
визначена у цій точці, і, якщо змінити значення 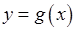 змінюється стрибковидно при переході через точку
змінюється стрибковидно при переході через точку 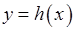 прямують до нескінченності при
прямують до нескінченності при  . А функція
. А функція  не визначена у точці
не визначена у точці  від висоти над рівнем моря
від висоти над рівнем моря  задається барометричною формулою:
задається барометричною формулою: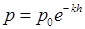 , де
, де  – додатні сталі. Графік цієї функції має вигляд
– додатні сталі. Графік цієї функції має вигляд
 від температури
від температури 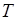 має приблизно лінійний характер, коли
має приблизно лінійний характер, коли 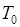 (своєї для кожного металу). Якщо
(своєї для кожного металу). Якщо  , то опір
, то опір  градуса за шкалою Кельвіна. Близьке до нього явище надтікучесті, коли деякі рідини при досягненні певної критичної температури (теж дуже низької; наприклад, для рідкого гелія вона складає 2,19 градусів за шкалою Кельвіна) майже повністю втрачають в’язкість.
градуса за шкалою Кельвіна. Близьке до нього явище надтікучесті, коли деякі рідини при досягненні певної критичної температури (теж дуже низької; наприклад, для рідкого гелія вона складає 2,19 градусів за шкалою Кельвіна) майже повністю втрачають в’язкість.
 , де
, де  – стала. Графік такої залежності має вигляд:
– стала. Графік такої залежності має вигляд:
 ,
, .
. », то можна означення неперервності функції у точці сформулювати так:
», то можна означення неперервності функції у точці сформулювати так: називається неперервною у точці
називається неперервною у точці  , і
, і 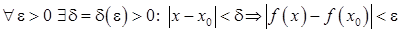 .
.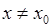 , або
, або 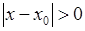 . Тобто функція могла бути невизначеною в точці
. Тобто функція могла бути невизначеною в точці 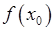 . У випадку неперервності ці особливості зникають. Функція визначена у точці
. У випадку неперервності ці особливості зникають. Функція визначена у точці  , можна третю умову неперервності записати так:
, можна третю умову неперервності записати так: .
. різницю
різницю  і назвемо цю величину приростом аргументу у точці
і назвемо цю величину приростом аргументу у точці 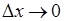 і навпаки. Різниця відповідних значень функції
і навпаки. Різниця відповідних значень функції  називається приростом функції у точці
називається приростом функції у точці  (рис. 44).
(рис. 44).

 .
. неперервна у будь якій точці числової прямої.
неперервна у будь якій точці числової прямої. і надамо нескінченно малий приріст
і надамо нескінченно малий приріст  .
. – нескінченно мала при
– нескінченно мала при 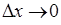 як добуток обмеженої функції
як добуток обмеженої функції  на нескінченно малу
на нескінченно малу  – нескінченно мала як добуток двох нескінченно малих. Отже
– нескінченно мала як добуток двох нескінченно малих. Отже 
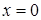 .
. , і
, і  виконано нерівність
виконано нерівність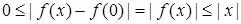 , оскільки
, оскільки  при
при 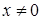 . Отже
. Отже  , тобто функція неперервна в точці
, тобто функція неперервна в точці  не є неперервною у точці
не є неперервною у точці  , а ця величина не є нескінченно малою при
, а ця величина не є нескінченно малою при  .
. неперервна в точці
неперервна в точці  , то ця функція обмежена в деякому околі точки
, то ця функція обмежена в деякому околі точки  , то існує окіл точки
, то існує окіл точки  .
.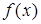 ,
,  неперервні в точці
неперервні в точці  ,
,  також неперервні в точці
також неперервні в точці  , то функція
, то функція  також неперервна в точці
також неперервна в точці  , а функція
, а функція  неперервна в точці
неперервна в точці  , то складена функція
, то складена функція  неперервна в точці
неперервна в точці 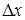 . Тоді функція
. Тоді функція 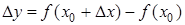 . Функція
. Функція  . Оскільки функція
. Оскільки функція 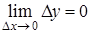 . А оскільки функція
. А оскільки функція  . Отже
. Отже
 , тобто функція
, тобто функція  неперервна в точці
неперервна в точці  таке, що функція
таке, що функція  , та існує
, та існує 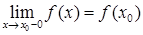 . Функція
. Функція  , та існує
, та існує  .
.


