
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дослідити функції та побудувати їхні графіки.Содержание книги
Поиск на нашем сайте
1.
1) Функція є многочленом, область існування якого – вся множина дійсних чисел.
2) Знайдемо точки перетину графіка с віссю Точки перетину з віссю 3) Функція не періодична, вона не є парною, не є непарною 4) Функція є неперервною на всій числовій прямій. Тобто точок розриву не має. 5) Досліджуємо функцію на монотонність та екстремум. Обчислимо Функція зростає на інтервалах Згідно з правилом знаходження екстремуму,
Обчислимо
Таким чином, екстремальні точки: 6) Знайдемо інтервали вгнутості та опуклості, точки перегину.
Розв’яжемо рівняння
Функція вгнута на інтервалі Значення
7) Знайдемо асимптоти заданої кривої. Вертикальних асимптот немає. З’ясуємо, чи є похилі асимптоти Обчислимо Отже, наша крива не має і похилих асимптот 8) Побудуємо графік функції.
2.
1) 2) Точки перетину графіка з координатними осями. При 3) Функція не періодична, вона непарна бо
4) В точці Отже, пряма 5) Знайдемо
Обчислимо
Отже, 6) Знайдемо Зважаючи на те, що
7) Вертикальну асимптоту ми вже знайшли: Обчислимо
Тоді пряма 8) Побудуємо графік.
3.
1) 2) Розглянемо перетин графіка з координатними осями. З віссю 3) Функція не періодична, але є парною, бо 4) Точок розриву функція не має. 5)

Функція зростає на інтервалі Точка Обчислимо Тобто точка екстремуму нашої функції 6) Знайдемо Дослідимо функцію на вгнутість та опуклість.
Функція вгнута на інтервалі Знайдемо Отже,
7) Вертикальних асимптот графік не має. Для похилих асимптот знайдемо
Будемо мати:
Отже, похилих асимптот не буде. 8) Будуємо графік.
4.
1) 2) Якщо 3) Функція не періодична, не є парною або непарною 4) Функція неперервна в області визначення, тому точок розриву не має. 5) Обчислимо З умови Будемо мати: Ф
Точка 6) Знайдемо Тоді
Функція вгнута на інтервалі Отже, у точці
Тому
7) Вертикальної асимптоти графік функції не має. Для похилих асимптот знайдемо Отримаємо:
Тому У випадку коли 8) Будуємо графік.
5.
1) Оскільки задана функція дробово-раціональна, то вона не існує в тих точках, де знаменник дорівнює нулю: Отже, 2) Нехай Нехай 3) Функція не періодична, вона непарна, тому що
Її графік є симетричним відносно початку координат. 4) Маємо дві точки розриву II-го роду: Отже, прямі 5) Знайдемо Розв’яжемо рівняння Помітимо, що похідна не існує при
Функція зростає на інтервалах Похідна змінює знак при переході через точки
Отже, екстремальні точки 6) Обчислимо
Розв’яжемо рівняння Помічаємо, що
При переході через
7) Вертикальні асимптоти:
Отже, рівняння похилої асимптоти: 8) Побудуємо графік функції.

Завдання для самостійної роботи Дослідити функції та побудувати їхні графіки:
1.
2. 3. 4. 5.
Розділ 2 ФУНКЦІЇ ДВОХ ЗМІННИХ
|
||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.227.250 (0.007 с.) |

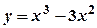 .
. .
. , для цього покладемо
, для цього покладемо  :
:  , звідки
, звідки  . Отже, в точках
. Отже, в точках  та
та  графік перетинає вісь
графік перетинає вісь  : покладемо
: покладемо  , тоді знайдемо
, тоді знайдемо  та
та 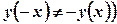 .
. . Знайдемо критичні точки з рівняння
. Знайдемо критичні точки з рівняння  :
:  або
або  . Отримаємо, що
. Отримаємо, що 
 та
та  .
. ; функція спадає на інтервалі
; функція спадає на інтервалі  .
. - точка максимуму,
- точка максимуму,  - точка мінімуму.
- точка мінімуму. ,
, .
. .
. .
. - критична точка другого роду.
- критична точка другого роду.
 та опукла на інтервалі
та опукла на інтервалі  .
. є абсцисою точки перегину. Знайдемо
є абсцисою точки перегину. Знайдемо  , тобто точка
, тобто точка  - точка перегину графіка.
- точка перегину графіка. .
.
 .
.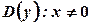 , тобто
, тобто 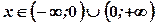 .
.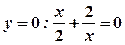

 , звідки
, звідки 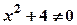 , тобто з віссю
, тобто з віссю  , робимо висновок, що графік не перетинає вісь
, робимо висновок, що графік не перетинає вісь 
 . Тому її графік є симетричним відносно початку координат.
. Тому її графік є симетричним відносно початку координат.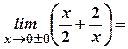
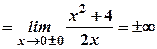 .
. . Розв’яжемо рівняння
. Розв’яжемо рівняння 
 ,
,  ,
, , звідки
, звідки  - критичні точки функції. Похідна не існує при
- критичні точки функції. Похідна не існує при  .
. Функція зростає на інтервалах
Функція зростає на інтервалах 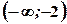 та
та  ; функція спадає на інтервалі
; функція спадає на інтервалі  .
.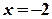 - точка максимуму функції, а
- точка максимуму функції, а  ,
, .
. ,
,  - екстремальні точки.
- екстремальні точки. .
. робимо висновок, що точок перегину графік функції не має.
робимо висновок, що точок перегину графік функції не має. Функція вгнута на інтервалі
Функція вгнута на інтервалі  та опукла на інтервалі
та опукла на інтервалі 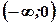 .
.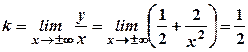 ,
, .
.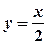 - похила асимптота.
- похила асимптота.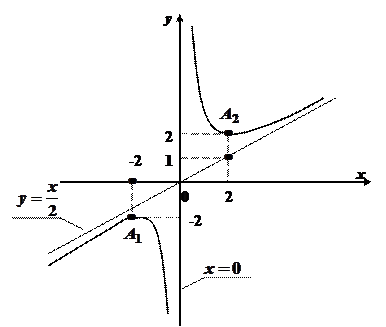
 .
. .
.
 , тобто у точці
, тобто у точці  графік перетинає вісь
графік перетинає вісь  . З віссю
. З віссю 
 , звідки
, звідки  або
або  . Зрозуміло, що остання рівність розв’язків не має. Отже, графік не перетинає вісь
. Зрозуміло, що остання рівність розв’язків не має. Отже, графік не перетинає вісь  .
. , тому її графік є симетричним відносно осі
, тому її графік є симетричним відносно осі  . Знайдемо критичні точки:
. Знайдемо критичні точки: 

 та спадає на інтервалі
та спадає на інтервалі  .
.


 .
. .
. .
. , звідки
, звідки  ,
, 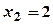 - критичні точки.
- критичні точки.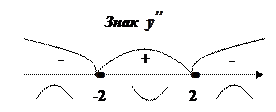
 та
та  ,
,  ,
,  .
. ,
,  - точки перегину.
- точки перегину. і
і 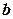 .
.
 ,
, .
.
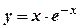 .
. . Якщо
. Якщо  , звідки
, звідки  , тому
, тому  .
.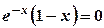
 , звідки
, звідки  ункція зростає на інтервалі
ункція зростає на інтервалі 
 .
. - екстремальна точка функції.
- екстремальна точка функції. .
. , тому
, тому  , звідки
, звідки 
 .
. .
. - точка перетину графіка функції.
- точка перетину графіка функції. ,
, .
. :
:  , тому ніякої асимптоти не буде.
, тому ніякої асимптоти не буде.
 .
. , звідки
, звідки 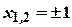 .
. .
. , звідки
, звідки 
 .
. та
та  , тому що
, тому що  та
та  .
. та
та  .
. , звідки
, звідки  - критичні точки функції.
- критичні точки функції. , але вони обидві не входять до області визначенності функції.
, але вони обидві не входять до області визначенності функції.
 , функція спадає на інтервалах
, функція спадає на інтервалах  .
. є точкою мінімуму функції, а
є точкою мінімуму функції, а 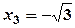 - точкою максимуму.
- точкою максимуму. ,
,  .
. ,
,  .
.

 .
. , звідки
, звідки  , а саме
, а саме  не існує при
не існує при  .
. Функція вгнута на інтервалах
Функція вгнута на інтервалах  , функція опукла на інтервалах
, функція опукла на інтервалах  .
. .Точка
.Точка  . Для похилих асимптот знайдемо
. Для похилих асимптот знайдемо  ,
, .
. .
. ;
; ;
; ;
;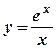 ;
; .
.


