
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повний диференціал функції. Похідні складених функційСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Повний приріст функції
де Повним диференціалом функції
де Для наближеного обчислення значення функції двох змінних користуються наближеною рівністю
Ця наближена рівність тим точніша, чим менше величини Нехай Похідну цієї функції знаходять за формулою
Зокрема, якщо
Нехай
Зразки розв’язування задач 1. Знайти повний диференціал функцій: а) Знайдемо частинні похідні:
За формулою (2.2) будемо мати:
б)
Отже, в)
г)
Тоді отримаємо:
2. Обчислити наближено за допомогою повного диференціала: Розглянемо функцію
Повний диференціал
Користуючись формулою (2.3), отримаємо: 3. Знайти Функція Будемо мати: Тоді шукана похідна запишеться у вигляді:
Підставляючи замість
4. Знайти Функція
Будемо мати: Тоді
5. Знайти Згідно з формулою (2.5):
Тоді Підставляючи замість
6. Знайти Функція Будемо мати: Знайдемо частинні похідні: Підставляючи, отримаємо:
Замінюючи
7. Знайти Як і в попередньому прикладі За формулами (2.6) маємо:
Завдання для самостійної роботи 1. Знайти повний диференціал функцій: а) б) в) 2. Обчислити наближено 3. Знайти 4. Знайти 5. Знайти
Частинні похідні вищих порядків. Похідні неявно заданих функцій Якщо задано функцію Частинні похідні від частинних похідних першого порядку називаються частинними похідними другого порядку. Вони позначаються:
Аналогічно означаються і позначаються частинні похідні вищих порядків. Частинні похідні, які відмінні одна від одної лише порядком диференціювання, називаються мішаними похідними. Вони є рівними між собою при умові їх неперервності, тобто Похідна від неявної функції, яку задано рівнянням
Частинні похідні неявної функції
Зразки розв’язування задач 1. Знайти частинні похідні другого порядку: а) Знайдемо перші похідні:
Знайдемо другі похідні:
б)
в)
2. Перевірити, що Знаходимо перші похідні:
Обчислимо мішані похідні другого порядку:
Як бачимо, 3. Перевірити, що функція Знайдемо частинні похідні першого та другого порядку, які є в даному рівнянні:
Підставляємо знайдені похідні в наше рівняння:
Отримаємо: Ми отримали тотожність, тому функція 4. Знайти похідну а)
Знайдемо частинні похідні: За формулою (2.7) маємо: б)
За формулою (2.7) маємо: в)
Тоді Отримаємо: 5. Знайти а)
Обчислимо Зауважимо, що у кожному випадку беручи похідну по одній змінній, дві другі вважаються сталими. За формулами (2.8) маємо: б)
Обчислимо Тоді будемо мати:
6.
Знайдемо За формулами (2.8):
Завдання для самостійної роботи
1. Знайти частинні похідні другого порядку: а) б) в) 2. Показати, що функція 3. 4. Знайти а) 5. Знайти
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 875; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

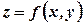 визначається за формулою
визначається за формулою , (2.1)
, (2.1) і
і  - прирости незалежних змінних.
- прирости незалежних змінних. , (2.2)
, (2.2) ,
,  .
. . (2.3)
. (2.3) і
і  .
. і
і  , кожна з яких, в свою чергу, є функцією незалежної змінної
, кожна з яких, в свою чергу, є функцією незалежної змінної  :
:  ,
,  . Тоді функція
. Тоді функція  є складеною функцією змінної
є складеною функцією змінної  . (2.4)
. (2.4) , то
, то . (2.5)
. (2.5) та
та  :
:  ,
,  . Тоді функція
. Тоді функція  є складеною функцією незалежних змінних
є складеною функцією незалежних змінних  (2.6)
(2.6) .
. ;
;  .
. .
. .
. ;
;  .
. .
. .
. ;
;  . Будемо мати:
. Будемо мати:  .
. .
. ;
; .
. .
. .
. , тоді
, тоді  ;
;  . Покладемо, що
. Покладемо, що  ,
,  , обчислимо
, обчислимо  ,
,  . Тоді
. Тоді  . Знаходимо частинні похідні і їх значення в точці
. Знаходимо частинні похідні і їх значення в точці  , а саме
, а саме , тоді
, тоді  ;
; , тоді
, тоді  .
. .
. , а саме:
, а саме:  .
. , якщо
, якщо 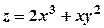 ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. .
. .
. , якщо
, якщо  ,
,  ,
,  .
. є складеною функцією змінної
є складеною функцією змінної  .
. ,
,  ,
,  ,
,  .
.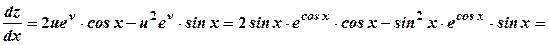
 .
. ,
,  .
. ,
, ,
, .
. .
.
 .
. і
і  , якщо
, якщо  ,
,  ,
,  .
. ,
, 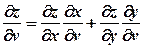 .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
, .
.
 ,
,
 .
. ,
,  ,
, 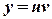 .
. - складена функція змінних
- складена функція змінних  ,
,  ,
, 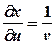 ,
,  ,
,  ,
,  .
.
 ,
, .
. ;
; ;
; .
. .
. ,
,  ,
,  .
. ,
,  .
. ,
,  ,
,  .
. і
і 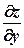 , то вони також є функціями незалежних змінних
, то вони також є функціями незалежних змінних  ,
,  ,
, ,
,  .
. .
.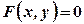 може бути обчислена за формулою:
може бути обчислена за формулою: . (2.7)
. (2.7) , заданої рівнянням
, заданої рівнянням  , можуть бути обчисленні за формулами:
, можуть бути обчисленні за формулами: ,
,  . (2.8)
. (2.8) .
. ,
,  .
. ,
,  ,
, ,
,  .
. .
. ,
,  ;
; ,
,  ,
, ,
,  .
. .
. ,
,  ;
;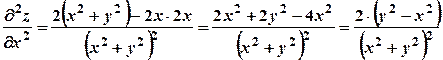 ,
, ,
, .
. .
. ,
,  .
. ,
, .
. задовольняє рівняння
задовольняє рівняння 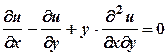 .
.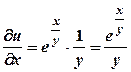 ,
,  ;
; .
. або
або  .
. , а саме
, а саме 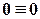 .
. від функцій, заданих неявно:
від функцій, заданих неявно: .
. .
. ,
,  .
. .
. .
. .
. ,
,  .
. .
. .
.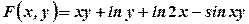 .
. ,
,  .
. .
. .
. .
. ,
,  ,
,  .
. ,
,  .
. .
. .
. ,
,  ,
,  .
. ,
, .
. . Знайти
. Знайти  та
та  у точці
у точці  .
. .
. ,
,  ,
,  .
. , тоді
, тоді  .
. , тоді
, тоді 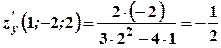 .
. ;
; ;
; .
. задовольняє рівняння
задовольняє рівняння 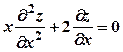 .
. . Знайти
. Знайти  ,
,  .
. ; б)
; б)  .
. .
.


