
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування диференціала в наближених обчисленняхСодержание книги
Поиск на нашем сайте
З означення похідної функції в точці Отже, при малих
Звідки Формула дозволяє знаходити значення функції де
Правило Лопіталя Правило Лопіталя для розкриття невизначеностей типу
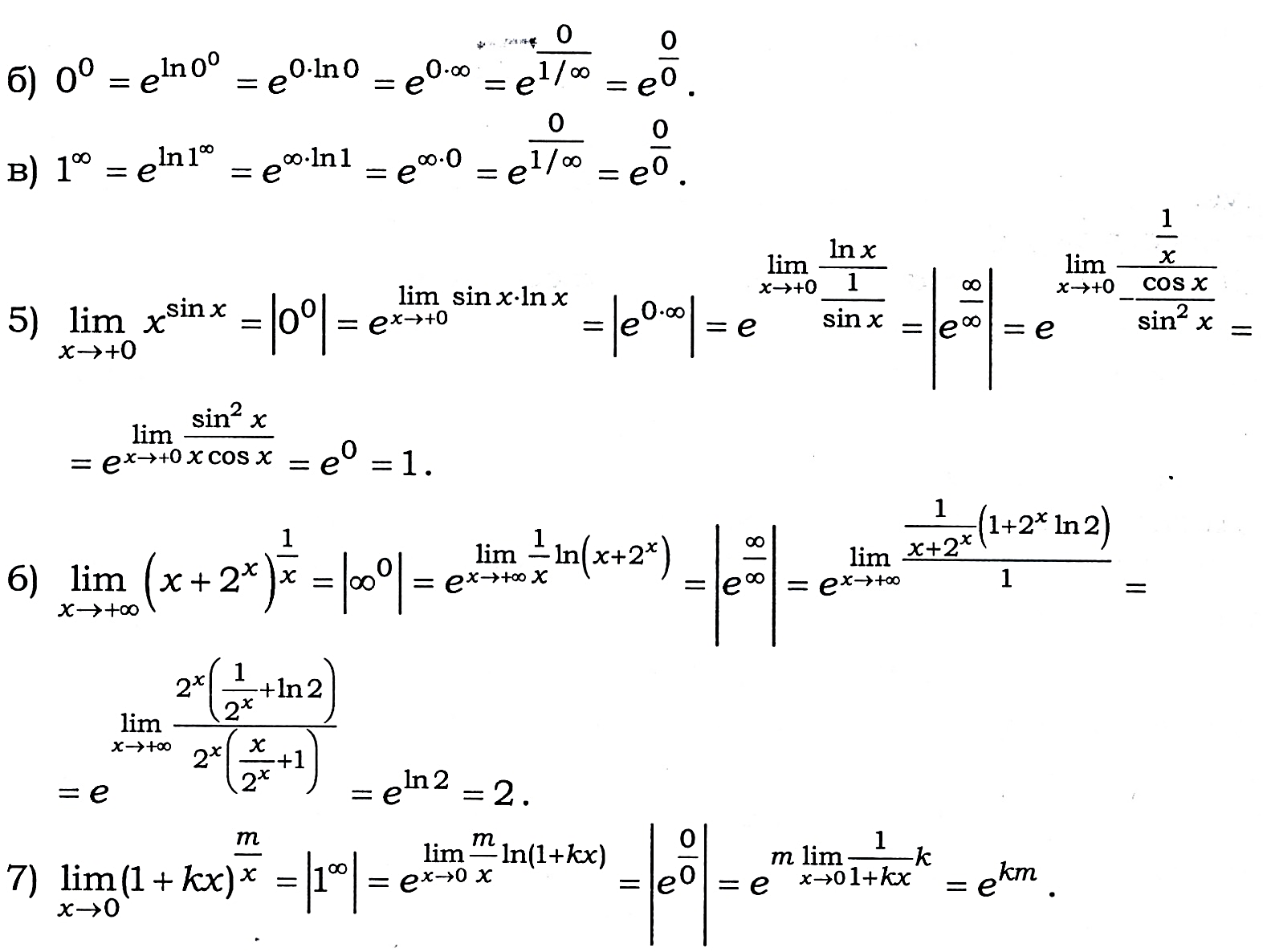
Приклади
Правило Лопіталя може застосовуватись послідовно декілька разів, якщо відношення похідних знову приводить до невизначеності, а самі похідні задовольняють умовам застосування правила Лопіталя.
Розкриття невизначеностей типу 0∙∞ і ∞-∞ проводять за допомогою тотожних перетворень, що приводять ці невизначеності до ви гляду
Розкриття невизначеностей типу ∞0, 00, 1∞ проводять із попереднім перетворенням степенево-показникового виразу за основною логарифмічною тотожністю У результаті цих дій отримаємо (формальний запис):
Екстремум функції. Функція f(х) називається зростаючою на інтервалі (а, Ь), якщо Якщо при Якщо Точка х0 називається точкою локального максимуму (мінімуму) функції у = f(х), якщо функції в деякому околі цієї точки. Точки локального максимуму і мінімуму функції називаються точками екстремуму цієї функції.
Дослідження функцій та побудова графіків. Загальна схема: Щоб дослідити функцію y = f(x) та побудувати її графік необхідно: 1) знайти область визначення функції, тобто множину всіх точок для яких існує значення функції; 2) знайти (якщо вони існують) точки перетину графіка з координатними осями. Для цього потрібно у рівняння y = f(x) підставити x=0, а також розв'язати рівняння f(x) = 0 для відшукання точок перетину з віссю Ox;
3) дослідити функцію на періодичність, парність і непарність. У деяких випадках це можна зробити візуально за самим виглядом функції, якщо ні- то проводимо перевірку: 1. f(-x) = f(x) – функція парна; 2. f(-x) = -f (x) – функція непарна; 3. f(x+T) = f(x)– функція періодична, T – період функції. Таким чином, якщо маємо парну функцію y= f(x), то достатньо побудувати її для додатніх значень x >0, після чого відобразити симетрично відносно осі абсцис y на решту області. У випадку непарної функції графік буде симетричний відносно початку координат. Для прикладу, якщомаємо непарну функцію, графік якої належить першій чверті другу половину отримаємо поворотом першої чверті на 180 градусів (третя чверть). Періодичними є переважно фукнкції, складені з простих тригонометричних та деякі параметрично задані функції. 4) знайти точки розриву та дослідити їх (такими точками є краї інтервалів визначення функції); 5) знайти інтервали монотонності, точки екстремумів та значення функції в цих точках; 6) знайти інтервали опуклості, вгнутості та точки перегину; 7) знайти асимптоти кривої; 8) побудувати графік функції.
Функції багатьох змінних. Як відомо, будь-який упорядкований набір з n дійсних чисел х1…,хn позначається (х1,…,хn) або М(х1,…,хn) і називається точкою n -вимірного арифметичного простору Rn; числа х1,…,хn називаються координатами точки М(х1,…,хn). Відстань між точками М(х1,…,хn) і М/(х/1,…,х/n) визначається за формулою Нехай D
яка визначає, взагалі кажучи, деяку поверхню в R3. Нехай (х01,…,х0k,…x0n) – довільна фіксована точка в області визначення функції u = f(х1,…,хn). Надаючи значенню змінної хk приросту
Ця границя називається частинною похідною 1-го порядку функції по змінній xk в точці (x01,…,x0n) і позначається
Аналогічно визначаються і позначаються частинні похідні порядку вищого, ніж другий. Функція u=f(M) називається диференційовною в точці М0, якщо скрізь в околі цієї точки певний приріст функції можна подати у вигляді
де Диференціалом 1-го порядку du функції Диференціал k -го порядку функції яка формально розкривається за біномним законом. Градієнт функції Прикладом функцій багатьох змінних в економіці э виробничі функції
Частинні похідні
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.220.221 (0.006 с.) |

 випливає, що її приріст
випливає, що її приріст 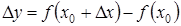 можна подати у вигляді:
можна подати у вигляді:  , де
, де  , якщо
, якщо 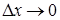 .
.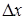 має місце наближена рівність:
має місце наближена рівність: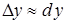 тобто
тобто 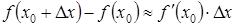 .
.
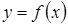 в точці
в точці 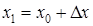 , якщо відомі значення
, якщо відомі значення 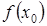 і
і  , з точністю
, з точністю  :
: 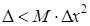
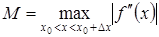 .
.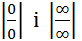 полягає в такому: якщо функції f(х) і g(х) нескінченно малі або нескінченно великі при х → а, диференційовані в околі точки х=а,g(x)≠0в околі цієї точки, існує
полягає в такому: якщо функції f(х) і g(х) нескінченно малі або нескінченно великі при х → а, диференційовані в околі точки х=а,g(x)≠0в околі цієї точки, існує  , то існує
, то існує 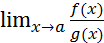 і справедлива рівність
і справедлива рівність
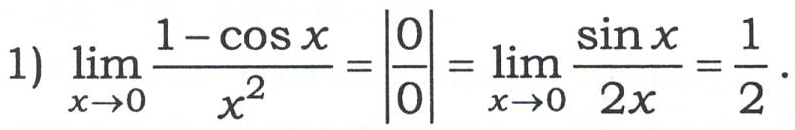
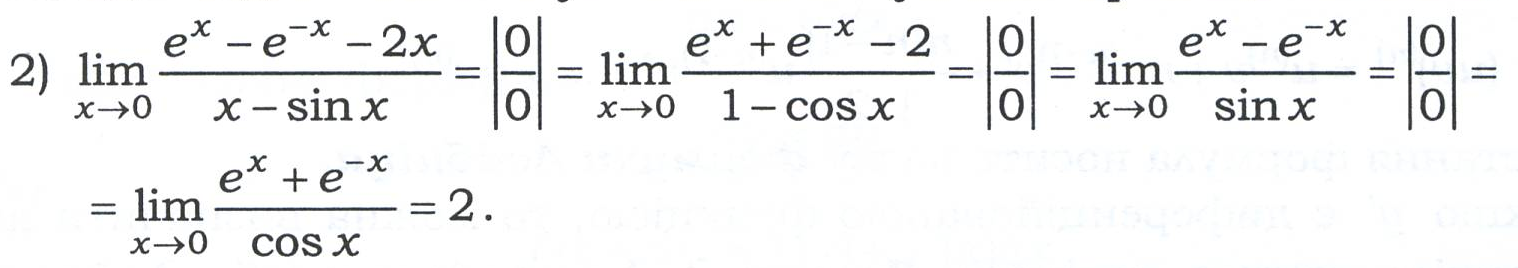
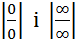 , а потім застосовують таблицю еквівалентних нескінченно малих величин і правило Лопіталя.
, а потім застосовують таблицю еквівалентних нескінченно малих величин і правило Лопіталя.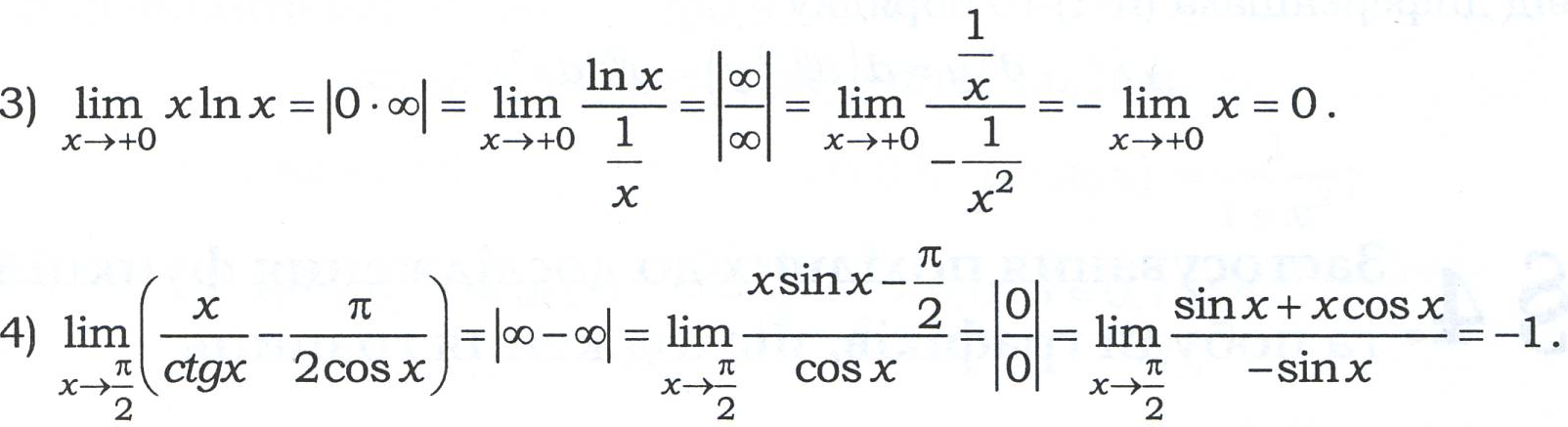
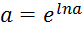
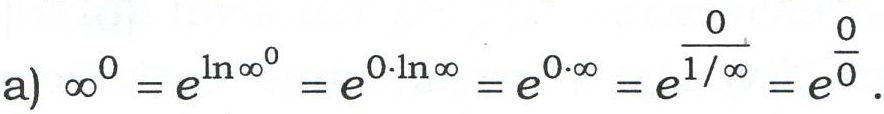
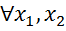 зцього інтервалу, таких, що
зцього інтервалу, таких, що 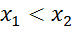 , виконується умова
, виконується умова 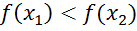 .
. , то функція називається спадною.
, то функція називається спадною. на (а,Ь), то функція на цьому інтервалі зростає. Якщо
на (а,Ь), то функція на цьому інтервалі зростає. Якщо 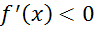 на (а,Ь), то функція на цьому інтервалі спадає.
на (а,Ь), то функція на цьому інтервалі спадає.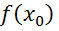 є найбільшим (найменшим) значенням
є найбільшим (найменшим) значенням
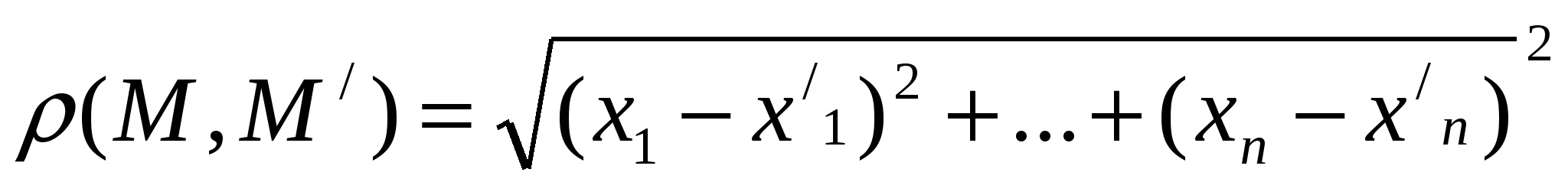
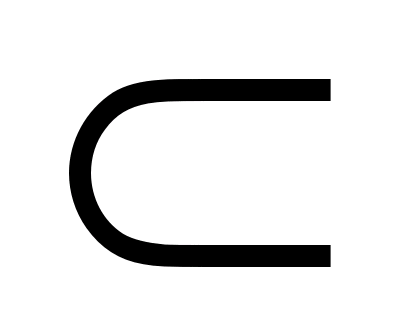 Rn – довільна множина n -вимірного арифметичного простору. Якщо кожній точці М(х1,…,хn)
Rn – довільна множина n -вимірного арифметичного простору. Якщо кожній точці М(х1,…,хn)  D поставлено у відповідність деяке цілком визначене дійсне число f(M)= f(х1,…,хn), то кажуть, що на множині D задана числова функція f: Rn
D поставлено у відповідність деяке цілком визначене дійсне число f(M)= f(х1,…,хn), то кажуть, що на множині D задана числова функція f: Rn  R від n змінних х1…,хn. Множина D називається областю визначення, а множина
R від n змінних х1…,хn. Множина D називається областю визначення, а множина  - множиною значень функції f. Зокрема, при n = 2 функцію двох змінних z = f(x,y),(x,y)
- множиною значень функції f. Зокрема, при n = 2 функцію двох змінних z = f(x,y),(x,y) 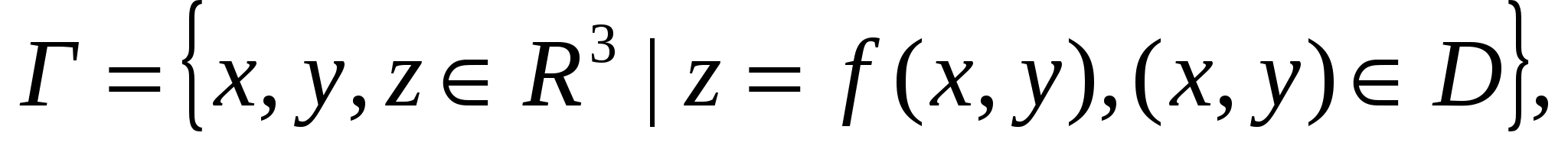
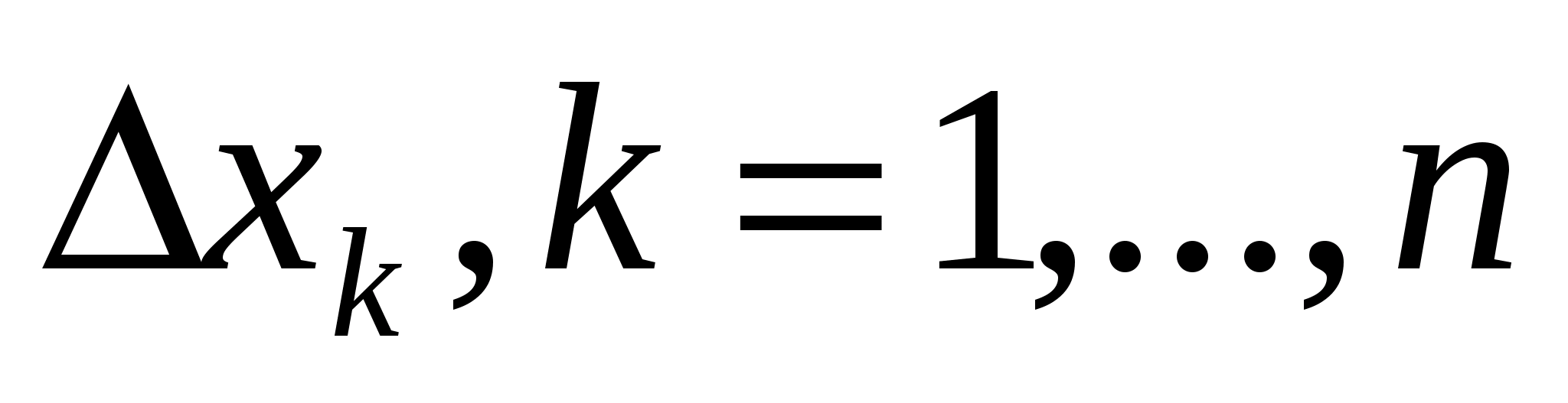 , розглянемо границю
, розглянемо границю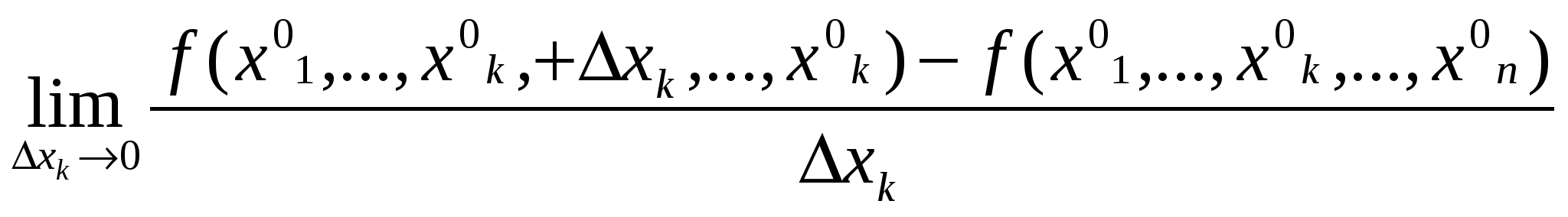 .
.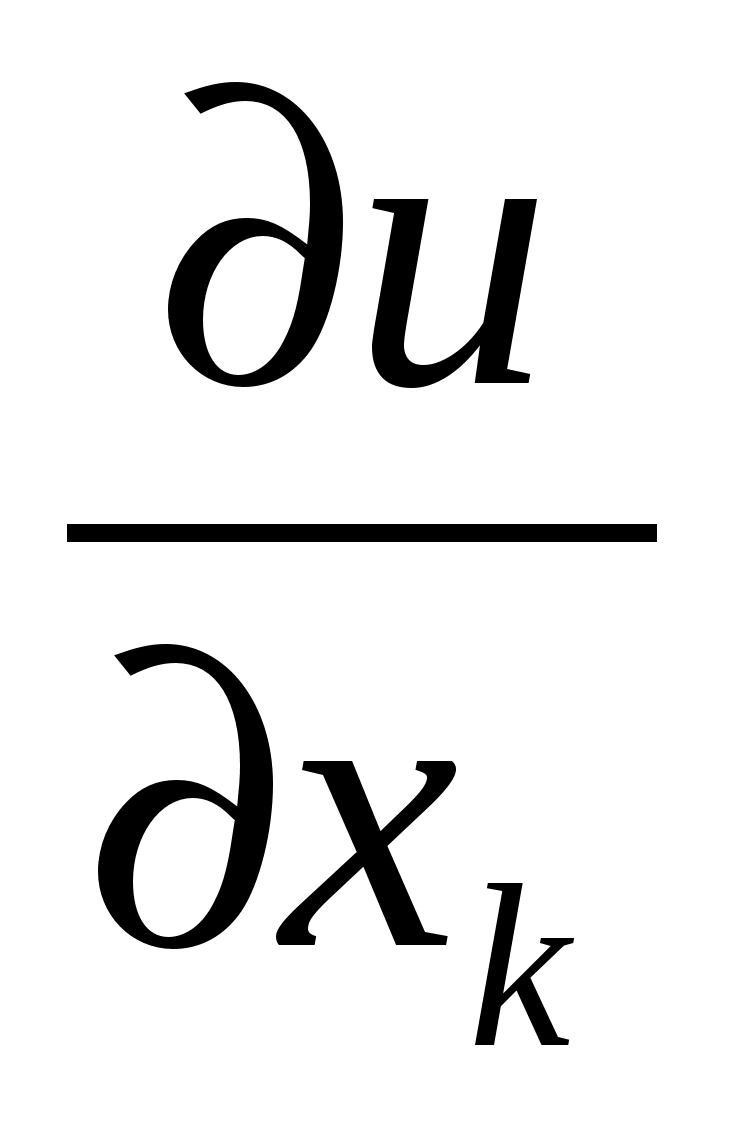 або
або  Похідні другого порядку позначаються так:
Похідні другого порядку позначаються так: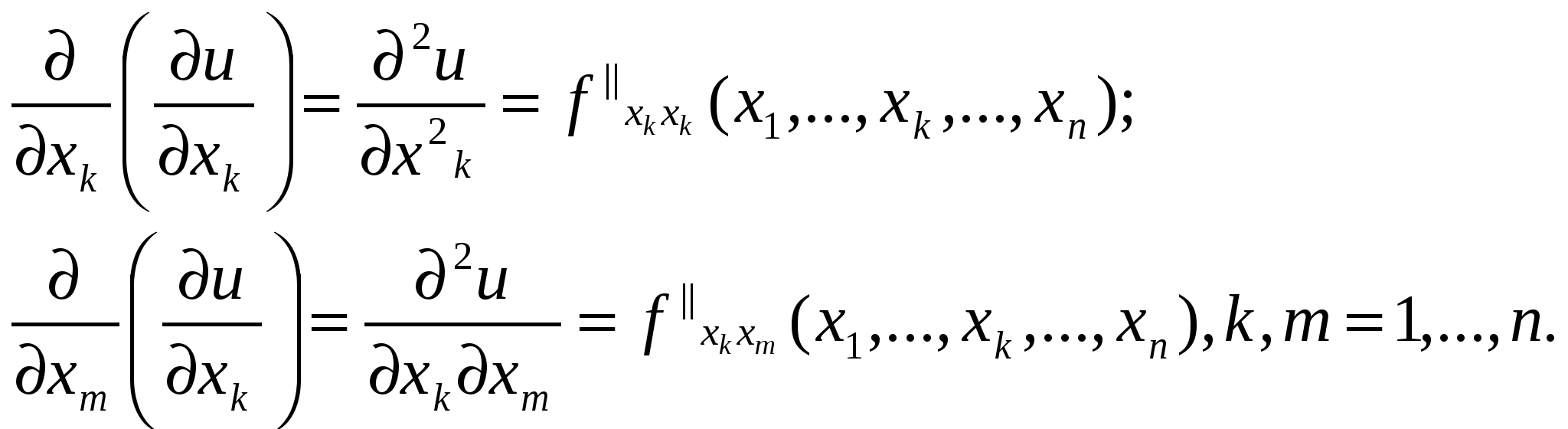
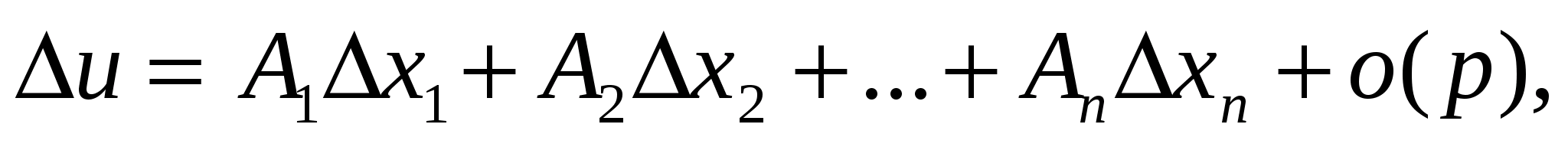
 A1,…An – числа, не залежні від
A1,…An – числа, не залежні від  .
.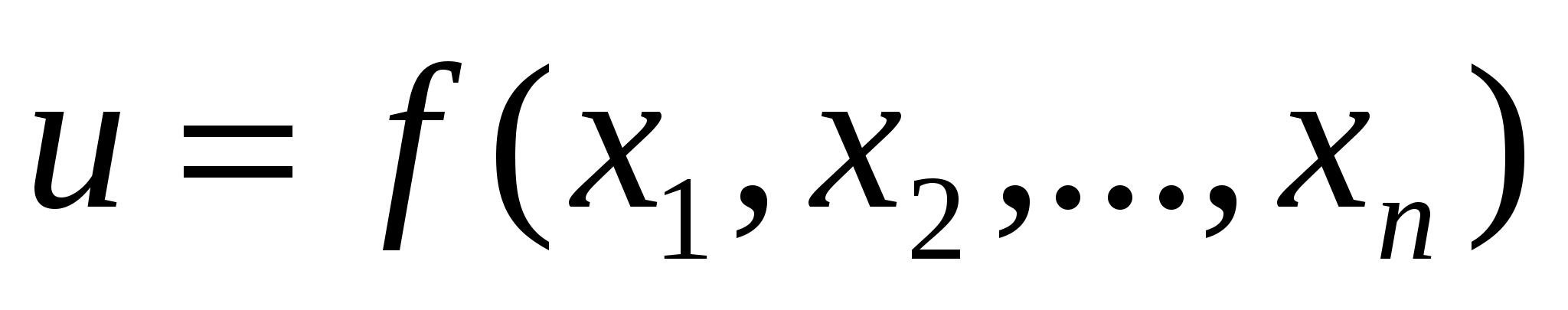 називається вираз
називається вираз 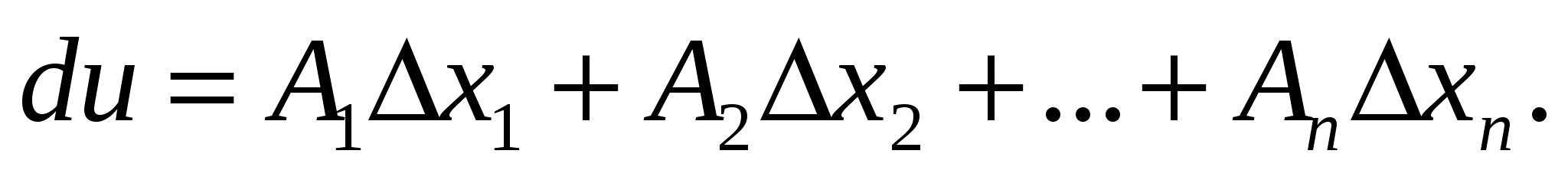
 , де х1…хn – незалежні змінні, символічно записуються у вигляді формули
, де х1…хn – незалежні змінні, символічно записуються у вигляді формули 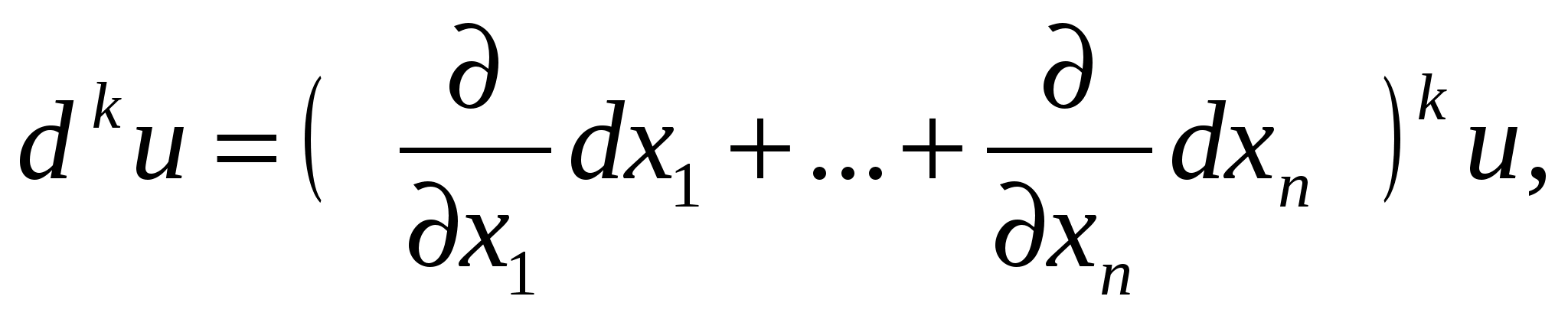
 - це вектор, що визначається формулою grad
- це вектор, що визначається формулою grad 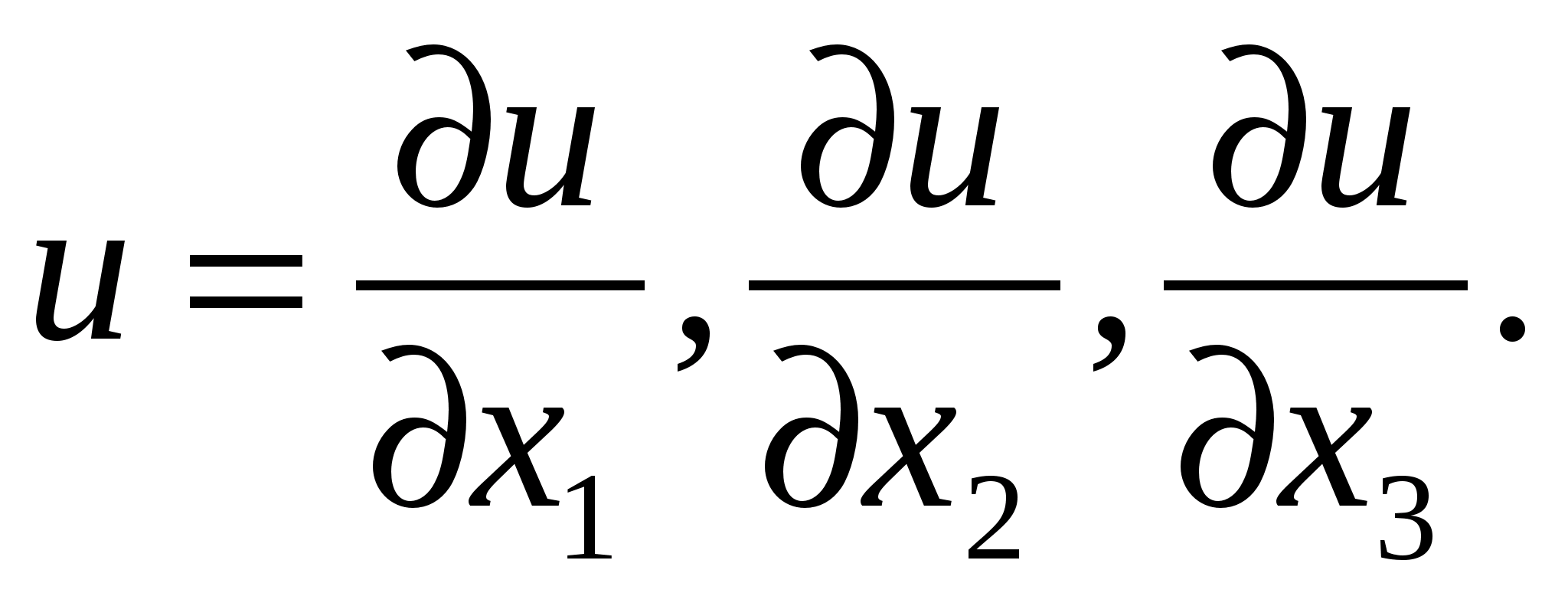 Він визначає напрямок найшвидшого зростання функції
Він визначає напрямок найшвидшого зростання функції




