
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Криві та поверхні другого порядкуСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Загальне рівняння кривої другого порядку: A Основні криві другого порядку: 1) Еліпс – це геометричне місце точок, сума відстаней до двох фіксованих точок площини (фокусів) є стала величина
2) Гіпербола – це геометричне місце точок для яких абсолютна величина різниці відстаней від фокусів є сталою
3) Парабола – називається геометричне місце точок для кожної з яких відстань до фіксованої точки площини (фокуса) дорівнює відстані до фіксованої прямої
Границя числової послідовності. Якщо кожному натуральному числу n є N за певним правилом ставиться у відповідність деяке дійсне число xn, то множину чисел {х1, х2, …, хn,...} називають послідовністю (числовою послідовністю) і позначають символом {хn}. Числа х1, х2, …, хn,... є членами (елементами) послідовності, хn - загальним членом послідовності. Число a називається границею послідовності {хn}, якщо для будь-якого числа ε > 0 можна знайти такий номер N = N (ε), що при всіх n > N(ε) виконується нерівність
При цьому пишуть Довільний інтервал вигляду (а - ε, а + ε), де ε > 0, називається ε - околом точки а. Якщо число а є границею послідовності {хn}, то для будь-якого ε > 0 можна знайти такий номер N = N(ε), що при n > N (ε) усі члени послідовності потраплять у ε - окіл точки а. Якщо послідовність має скінченну границю, то вона називається збіжною. Якщо послідовність не збігається, то кажуть, що вона є розбіжною. Послідовність {хn} називається обмеженою, якщо існує таке число С > 0, що при всіх nєN виконується нерівність Послідовність {хn} називається обмеженою зверху (знизу), якщо існує таке число М(m), що при всіх nєN виконується нерівність xn ≤ M (xn ≥ m). Послідовність {хn} називається зростаючою (спадною), якщо для будь-якого nєN виконується нерівність xn+1 > хn (xn+1 < хn). Послідовність {хn} називається неспадною (незростаючою), якщо для будь-якого nєN виконується нерівність xn+1 ≥ хn (xn+1 ≤ хn). Неспадні і незростаючі послідовності називаються монотонними, а зростаючі й спадні - строго монотонними. Нехай {хn} - деяка числова послідовність, а n1 < n2 <... < nk <... - зростаюча послідовність натуральних чисел. Тоді послідовність Послідовність {хn} називається фундаментальною, якщо для будь-якого числа ε > 0 можна знайти такий номер N, що при всіх n > N, m > N виконуватиметься нерівність Нескінченно малі та нескінченно великі послідовності. Якщо послідовність має скінченну границю, то вона називається збіжною. Якщо послідовність не збігається, то кажуть, що вона є розбіжною. Збіжну до нуля послідовність називають нескінченно малою. Послідовність {хn} називається нескінченно великою, якщо для будь-якого числа Е > 0 можна знайти такий номер N, що при всіх n > N виконуватиметься нерівність Позначається це так: Границя функції. Нехай функція Визначення 1. (Гейне ). Число Якщо число A– границя функції в точці Нехай функція Визначення 2. (Коші). Число A називається границею функції
виконується нерівність
Визначення границі функції в точці за Гейне і за Коші еквівалентні.
Неперервність функції
Точки розриву
Похідна функції. Похідною функції
Похідна може позначатись
Правила диференціювання Нехай функції 1. Похідна від суми (різниці) двох функцій: 2. Похідна від добутку двох функцій: 3. Похідна від частки двох функцій: 4. Похідна складної функції: якщо
17.Таблиця похідних
Диференціал
19.Похідні вищих порядків, диференціали. Нехай функція у = f(х) визначена та має похідну першого порядку на інтервалі (а,Ь). Тоді її похідна у' = f '(х) також буде функцією, що визначена на інтервалі (а,Ь). Якщо ця функція сама є диференційованою в деякій точці х інтервалу (а,Ь), тобто має в цій точці похідну, то вказана похідна називається другою похідною або похідною 2-го порядку і позначається
Аналогічно можна ввести поняття третьої похідної, потім четвертої і т.д. Похідною п-го порядку називається похідна від похідної (n-І)-го порядку і позначається
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

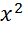 + Bxy + C
+ Bxy + C  + Dx + Ey = F = 0
+ Dx + Ey = F = 0 +
+  = 1
= 1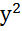 = 2рх – канонічне рівняння параболи
= 2рх – канонічне рівняння параболи
 або
або  .
. < С. У протилежному випадку послідовність називається необмеженою.
< С. У протилежному випадку послідовність називається необмеженою.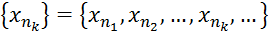 називається підпослідовністю послідовності {хn}.
називається підпослідовністю послідовності {хn}. .
. або
або  ,
,  .
. визначена на деякій підмножині
визначена на деякій підмножині  множини дійсних чисел
множини дійсних чисел  ,і
,і 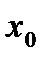 – гранична точка множини
– гранична точка множини 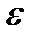 –околі
–околі  граничної точки
граничної точки  називається границею функції
називається границею функції  при
при  (або в точці
(або в точці  , збіжної до
, збіжної до  збіжна до
збіжна до  .
. або
або  при
при  має границю
має границю  при
при  (або в точці
(або в точці 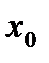 ), якщо для будь-якого
), якщо для будь-якого  можна знайти таке число
можна знайти таке число  , що при всіх
, що при всіх  , які задовольняють нерівність
, які задовольняють нерівність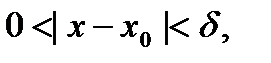

 Друга чудова границя та її наслідки.
Друга чудова границя та її наслідки.



 в точці
в точці  називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.

 мають у певній точці
мають у певній точці  похідні
похідні 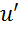 ,
, 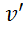 .
.



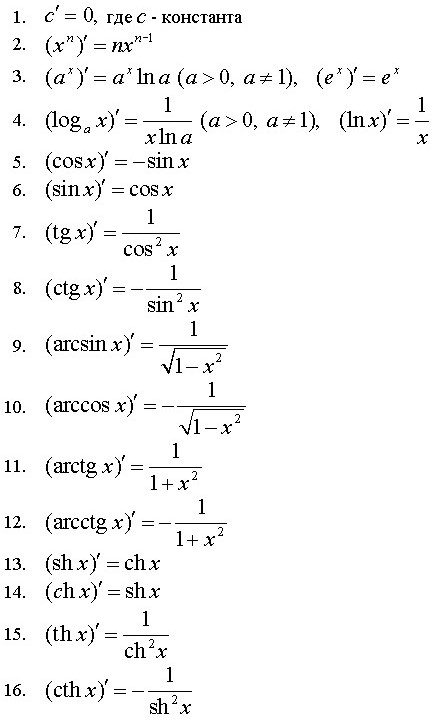

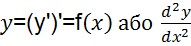 .
.




