Числові ряди з невід’ємними членами

Означення: числовим рядом є вираз, який має вигляд суми нескінченої послідовності доданків: U₁+U₂+U₃+…+U_n+…(1), де U₁ – перший член ряду, U₂ – другий, а U_n – n-член, або загальний член ряду.

Утворимо так звані часткові суми ряду:

S₁=U₁

S₂=U₁+U₂

…………………………

S_n=U₁+U₂+U₃+…+U_n+...

…………………………

Означення: Ряд (1) називають збіжним, якщо:

тобто сума існує. Ряд (1) коротко можна записати:

(1)

 

Якщо ряд (1) збіжний, то пишуть:

 

Означення: якщо:

то ряд (1) називають розбіжним рядом, такий ряд суми не має.

Різницю між сумою S ряду і n-початковою сумою називають залишком ряду і позначають:

Rn=S-Sn. Якщо ряд збіжний, то:

Необхідна ознака збіжності.

Теорема: Якщо ряд

збіжний, то:

Доведення: Оскільки ряд збіжний, то:

поряд з цією рівністю для збіжного ряду можна записати:

Ця ознака є лише необхідною умовою збіжності. Якщо вона не виконується, то ряд розбіжний, якщо виконується, то ряд може бути як збіжним, так і розбіжним.

Достатня ознака збіжності для знакододатних рядів.

(Ознака порівняння рядів; ознака Даламбера; радикальна ознака Коші; інтегральна ознака Коші)

Означення: знакододатний ряд – ряд вигляду U₁+U₂+…+U_n+…, всі члени якого є додатними.

1) Ознака порівняння рядів.

Складаємо геометричний прогресію або гармонійний ряд і порівнюємо. Якщо порівняємо з розбіжним рядом, всі члени якого менше відповідних членів шуканого ряду, то шуканий ряд – теж розбіжний, якщо більшіші, то шуканий ряд – збіжний. Якщо порівнюємо із збіжним рядом, всі члени якого більше відповідних членів шуканого ряду, то шуканий ряд – теж збіжний, якщо менші, то шуканий ряд є розбіжним.

Гармонійний ряд – ряд вигляду:

Приклад:

Порівнюємо з гармонійним рядом, який є розбіжний.

маємо:

 

ÞРяд розбіжний.

2) Ознака Даламбера:

Якщо для знакододатного ряду

існує

то, якщо:

а)D>1, ряд – розбіжний

б)D<1, ряд – збіжний

в)D=1, –???

 

3) Радикальна ознака Коші.

а)k<1, ряд – збіжний

б)k>1, ряд – розбіжний

в)k=1, –???

 

4) Інтегральна ознака Коші.

Беремо ò від Un-члена ряду. Якщо невласний інтеграл збіжний, то ряд – збіжний, якщо ж розбіжний, то ряд – розбіжний.

Знакопочергові ряди. Ознака Лейбніца.

Означення: Знакопочерговий ряд – ряд вигляду:

Для дослідження знакопочергового ряду на абсолютну і умовну збіжність складається ряд з абсолютних величин.

Означення: Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду.

Означення: Знакозмінний ряд називається умовно збіжним, якщо цей ряд збігається, а ряд із абсолютних величин його членів розбігається.

Ознака Лейбніца.

Теорема: Якщо члени знакопочергового ряду спадають по абсолютній величині і границя абсолютної величини загального члена ряду = 0, то ряд збігається. Коротко цю теорему можна записати так:

Наслідок1:

Знак суми збіжного знакопочергового ряду такий же, як і знак першого члену ряду.

Наслідок2:

Якщо знакопочерговий ряд збігається, то його сума за абсолютною величиною не перевищує перший член ряду, тобто |S|<|U₁|.

Наслідок3:

Якщо при обчисленні суми збіжного знакопочергового ряду обмежитись тільки першими n членами, а всі інші відкинути, то похибка за абсолютною величиною не перевищить першого із відкинутих членів.

Наслідок4:

Якщо для ряду не виконується умова теореми Лейбніца:

то ряд є розбіжним, оскільки не виконується необхідна умова збіжності.

Функціональні ряди.

Означення: Ряд вигляду U₁(x)+U₂(x)+…+U_n(x)+…, де членами рядуU_n(x) є ф-ції від аргументу х, називається функціональним рядом. При х=х₀ функціональний ряд перетворюється на на числовий ряд.

Означення: Всі значення аргументу х, при яких функціональний ряд збігається, називаються областю збіжності функціонального ряду.

Степеневі ряди:

Означення: Функціональний ряд вигляду a₀+a₁x+a₂x²+…+a_nxⁿ+… називається степеневим рядом, його загальний член U_n(x)=a_nxⁿ, а числа а₀,а₁,а_2,...,а_n,... – називають коефіцієнтами степеневого ряду. Степеневий ряд можна записати як:

Степеневий ряд може мати вигляд: a₀+a₁₍x-с)+a₂₍x-с)²+…+a_n(x-с)ⁿ+… Такий ряд за допомогою заміни х-с=у зводиться до звичайного степеневого ряду.

 

 

51. Знакозмінні ряди.

Функціональні ряди.

Вираз називається функціональним рядом. Приклад При одних значеннях ряд може сходитися, для інших значень - розходитися.При кожному конкретному значенні із області визначення D функціональний ряд перетворюється на числовий. Якщо для є D числовий ряд збігається, то кажуть, що функціональний ряд збігається в точці , а саму точку називають точкою збіжності. Множина всіх значень змінної , при яких функціональний ряд збігається називається областю збіжності ряду.

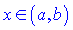Ознака Вайєрштраса. Функціональний ряд вигляду абсолютно і рівномірно збіжний на проміжк , якщо існує знакододатний збіжний числовий ряд такий, що для всіх виконується умова

Теорема Абеля. Якщо степеневий ряд збігається в точці , то він збігається абсолютно в інтервалі Якщо степеневий ряд розбіжний в точці , то він буде розбіжний для всіх , що задовольняють умову

Число називають радіусом збіжності степеневого ряду, а проміжок - інтервалом збіжності (областю збіжності).Якщо всі коефіцієнти ряду ненульові, то радіус збіжності рівний наступній границі при умові, що вона існує (скінченна чи нескінченна).Для рядів вигляду

радіус збіжності визначається за формулою , проте інтервал збіжності з нерівності Теорема не дає відповіді про збіжність на кінцях інтервалу, тому їх слід перевіряти окремо за відомими ознаками збіжності.

 

53. Степеневі ряди.