
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціал функцій багатьох змінних.Содержание книги Поиск на нашем сайте
Різниця
Прирости незалежних змінних де
Похідна за напрямом.Градієнт. Похідною функції
Диференціювання складної функції
Диференціювання неявних функцій
Екстремуми функцій багатьох змінних Функція
Умовний екстремум
32. Найбільше та найменше значення функції в замкненій області
33. Первісна функція та невизначений інтеграл
Таблиця інтегралів
35. Основні методи інтегрування: метод підстановки, інтегрування частинами
36. Інтегрування раціональних дробів
Інтегрування деяких видів ірраціональностей
Інтегрування тригонометричних функцій Розглянемо ò R(sin x,cos x)dx, де R – раціональна ф-ія відносно sin, cos, тобто над sin, cos викон. лише арифметичні дії та піднесення до цілого степеня. Існують такі підстановки, що за їх допомогою інтеграл ò R(sinx,cosx)dx завжди може бути зведений до інтеграла від раціональної ф-ії ò R*(t)dt, загальна схема інтегрування якої розроблена. 1) Універсальна тригонометрична підстановка 2) Підінтегральна ф-ія – непарна відносно sin x, тоді роблять підстановку cos x = t.
3) Підінтегральна ф-ія – непарна відносно cos x раціоналізується за допомогою підстановки sin x = t. 4) Підінтегральна ф-ія R(sin x, cos x) – парна по sinx, cosx сукупно, тобто R(-sinx,-cosx)=R(sinx,cosx). В цьому випадку використовують підстановку tgx=t або ctgx=t. 5) Підінтегральна ф-ія R(tgx) раціоналізується підстановкою tgx=t. В інтегралах ò sin2nx×cos2mxdx рекомендується скористатися формулами зниження степеня. Визначений інтеграл Означення: Якщо існує скінченна границя інтегральних сум Sn при lіà0 і не залежить ні від способу розбиття [a;b] на частини Dхі, ні від вибору точок xі, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається:
За означенням, визначений інтеграл Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною. Формула Ньютона-Лейбніца Теорема (Ньютона-Лейбніца): Якщо ф-ія f(x) – неперервна для xÎ [a;b], то визначений інтеграл від ф-ії f(x) на проміжку [a;b] дорівнює приросту первісної ф-ії f(x) на цьому проміжку, тобто:
Зв’язок між визначеним та невизначеним інтегралами можна представити такою рівністю:
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1007; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.008 с.) |

 називається повним приростом функції
називається повним приростом функції 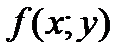 ,а різниці
,а різниці 
 називаються частинними приростами функції
називаються частинними приростами функції  Якщо функція
Якщо функція  і
і  , то, очевидно,
, то, очевидно,  ,
,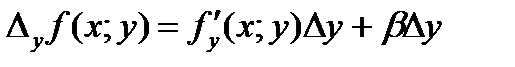 , де
, де 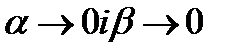 при
при 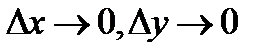 .Добутки
.Добутки  і
і  називаються частинними диференціалами функції
називаються частинними диференціалами функції  , то сума частинних диференціалів
, то сума частинних диференціалів  називається повним диференціалом функції
називається повним диференціалом функції 
 звичайно позначають
звичайно позначають  і
і 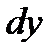 . Тоді
. Тоді  Можна показати, що
Можна показати, що  ,
,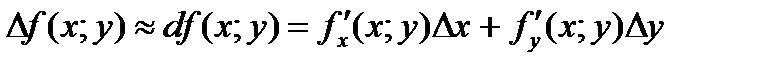
 в точці M(x,y) за напрямком вектора
в точці M(x,y) за напрямком вектора  називається границя
називається границя


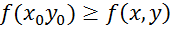 (відповідно нерівність
(відповідно нерівність ).
).
















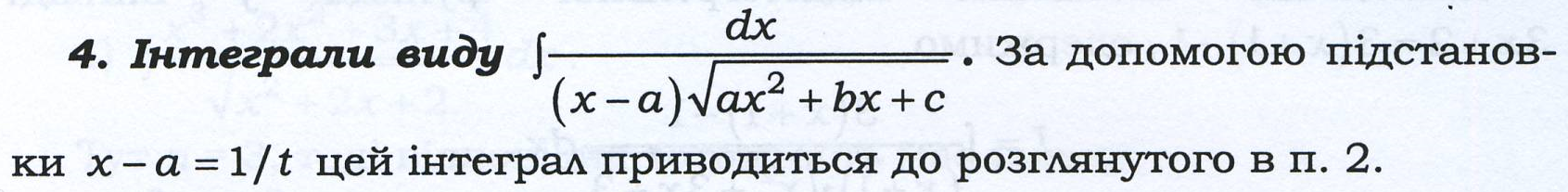
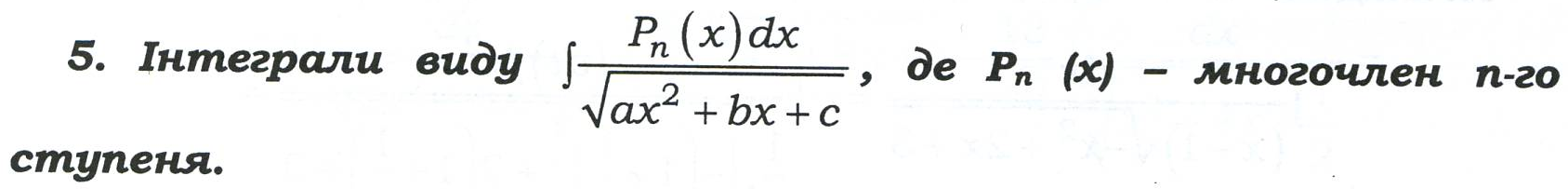


 . На практиці універсальну тригонометричну підстановку використовують, якщо sin x, cos x входять в невисокому степені, інакше підрахунки будуть складні.
. На практиці універсальну тригонометричну підстановку використовують, якщо sin x, cos x входять в невисокому степені, інакше підрахунки будуть складні.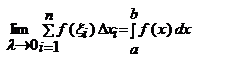
 – число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування. Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.
– число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування. Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції. де F’(x)=f(x)
де F’(x)=f(x)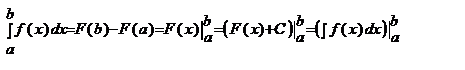 Наслідок: Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральної ф-ії і виконати над нею подвійну підстановку.
Наслідок: Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральної ф-ії і виконати над нею подвійну підстановку.


