
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування диференціального численняСодержание книги
Поиск на нашем сайте
З М І С Т Розділ 1 Застосування диференціального числення Для дослідження функцій 1.1. Зростання і спадання функції………………………………………………….5 1.2. Локальний екстремум функції………………………………………………..9 1.3. Опуклість і вгнутість кривих. Точки перегину……………………………...14 1.4. Асимптоти кривих……………………………………………………………..21 1.5. Схема дослідження функції та побудова її графіка…………………………22 Розділ 2 Функції двох змінних 2.1. Означення та область визначення. Частинні похідні першого порядку………………………………………….. 34 2.2. Повний диференціал функції. Похідні складених функцій………………………………………………….. 41 2.3. Частинні похідні вищих порядків. Похідні неявно заданих функцій…………………………………………….. 46 2.4. Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох змінних……………………………………………. 51 Розділ 3 Невизначений інтеграл 3.1. Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування………………………………………. 54 3.2. Метод підстановки (заміни змінної)………………………………………… 58 3.3. Метод інтегрування частинами……………………………………………… 62 3.4. Інтегрування раціональних функцій………………………………………… 66 3.5. Інтегрування функцій, раціонально залежних від тригонометричних…………………………………………………………74 3.6. Інтегрування деяких іраціональних функцій………………………………...82
ЛІТЕРАТУРА..........................................................................................................89 Вступ Основна форма навчання студентів – самостійна робота над навчальним матеріалом, яка складається з вивчення теоретичних положень за підручником, розгляду прикладів і розв’язання задач. При вивченні матеріалу за підручником треба переходити до наступного питання тільки після правильного зрозуміння попереднього, виконуючи на папері усі обчислення, навіть і ті, які пропущені у підручнику. Розв’язання задач при вивченні дисципліни «Вища математика» часто пов’язано з багатьма складностями. Якщо складається скрутне становище при розв’язанні задачі, то треба вказати характер цього утруднення, привести припущення відносно плану розв’язку. Відомо, що при самостійному розв’язуванні задач студентам потрібні постійні консультації щодо способів їх розв’язування, оскільки знайти шлях до розв’язування задачі без допомоги викладача або відповідного підручника студентові не під силу. Допомогти студентам технічних спеціальностей всіх форм навчання подолати ці складності, навчити їх застосовувати теоретичні знання до розв’язування задач - основне призначення цього навчального посібника.
У третій частині навчального посібника викладено матеріал з таких розділів вищої математики: «Визначений інтеграл», «Невласні інтеграли» та «Застосування визначеного інтеграла до задач геометрії». Основні теоретичні положення, формули та теореми ілюструються докладним розв’язанням великої кількості задач різного ступеня складності з їх повним аналізом. Для ефективності засвоєння матеріалу пропонуються завдання для самостійної роботи. Автори сподіваються, що саме така побудова посібника надає студентові широкі можливості до активної самостійної роботи, яка, безумовно, сприятиме засвоєнню матеріалу при вивченні дисципліни «Вища математика».
Розділ 1 ЗАСТОСУВАННЯ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ ДЛЯ ДОСЛІДЖЕННЯ ФУНКЦІЙ Зразки розв’язування задач Локальний екстремум функції Точка Правило знаходження екстремумів (максимумів і мінімумів) за допомогою першої похідної: 1) знайти область визначення 2) знайти похідну 3) знайти критичні точки; 4) дослідити знак При цьому критична точка 5) обчислити значення функції в точках екстремуму (екстремуми).
Зразки розв’язування задач Знайти екстремуми функцій. 1. 1) Область визначення 2) 3) Критичні точки:
4) Знаки
При переході через точку
5) 2. 1) Область визначення функції 2) 3) Критичні точки:
4) Знаки
При переході через точку 5) 3. 1) Область визначення 2)
3) Критичні точки:
4) Знаки
При переході через точки 5) Так як функція
4. 1) 2) 3) Критичні точки:
Функція
4) Знаки
Функція має дві екстремальні точки:
5)
5. 1) Область визначення 2)
3) Критичні точки: а) б) 4) Знаки
При переході через точку 5)
6. 1) 2) 3) Критичні точки: а) б) 4)Знаки
При переході через точку
5) 7. 1) Область визначення 2) 3) Критичні точки: а) б) 4) Знаки
5)
8. 1) Область визначення 2) 3) Критичні точки: а) б) Отже, критичних точок не має і функція не має екстремумів.
Завдання для самостійної роботи Знайти екстремуми функцій: 1.
2.
3. 4.
5. Зразки розв’язування задач Асимптоти кривих Пряма називається асимптотою кривої, якщо точка кривої необмежено наближується до неї при віддалені її від початку координат. Розрізняють вертикальні, похилі (горизонтальні) асимптоти. а) Вертикальні асимптоти. Графік функції б) Похилі асимптоти. Рівняння похилої асимптоти Слід окремо розглянути випадки, коли
Зразки розв’язування задач Знайти асимптоти кривих. 1. а) В точці Отже, б) Знайдемо похилі асимптоти:
Тоді 2. а) Область визначення функції:
В точках б) Знайдемо похилі асимптоти:
3. а) Область визначення функції:
Обчислимо Отже, б) Похилі асимптоти:
Маємо:
4. а) Область визначення функції Точок розриву II роду немає, тому графік функції не має вертикальних асимптот. б) Знайдемо похилі асимптоти:
При
5. а) Область визначення функції:
Обчислимо б) Похилих асимптот немає, тому що неможливо обчислити коефіцієнти
Завдання для самостійної роботи Знайти асимптоти кривих: 1. 2. 3. 4. 5. 6. 7. Зразки розв’язування задач Розділ 2 ФУНКЦІЇ ДВОХ ЗМІННИХ Зразки розв’язування задач 1. Знайти та зобразити області визначення функцій двох змінних: а) Функція не визначена лише тоді, коли б) Функція визначена при умові
в)
г) z Областю визначення цієї функції є сукупність пар
2. Знайти частинні похідні функцій: а) Функція
б) Вважаючи, що Якщо, в)
г)
д) При диференціюванні по
При диференціюванні по
є) Аналогічно попередньому прикладу маємо:
ж) При знаходженні частинних похідних
з) При диференціюванні по і) Аналогічно попередньому прикладу маємо: по к) Обчислюючи Обчислюючи похідну л)
м)
н)
3. Довести, що функція Знайдемо частинні похідні функції
Підставимо саму функцію
Будемо мати:
Отримано тотожність, це означає, що функція
Завдання для самостійної роботи 1. Знайти область визначення функцій: а) 2. Знайти частинні похідні функцій: а) б) в) г) д) є) ж) з)
3. Довести, що функція Зразки розв’язування задач 1. Знайти повний диференціал функцій: а) Знайдемо частинні похідні:
За формулою (2.2) будемо мати:
б)
Отже, в)
г)
Тоді отримаємо:
2. Обчислити наближено за допомогою повного диференціала: Розглянемо функцію
Повний диференціал
Користуючись формулою (2.3), отримаємо: 3. Знайти Функція Будемо мати: Тоді шукана похідна запишеться у вигляді:
Підставляючи замість
4. Знайти Функція
Будемо мати: Тоді
5. Знайти Згідно з формулою (2.5):
Тоді Підставляючи замість
6. Знайти Функція Будемо мати: Знайдемо частинні похідні: Підставляючи, отримаємо:
Замінюючи
7. Знайти Як і в попередньому прикладі За формулами (2.6) маємо:
Завдання для самостійної роботи 1. Знайти повний диференціал функцій: а) б) в) 2. Обчислити наближено |

 називається точкою максимуму (або мінімуму) функції
називається точкою максимуму (або мінімуму) функції  , якщо існує такий окіл
, якщо існує такий окіл  <
< 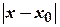 <
<  цієї точки, який належить області визначення функції, і для всіх
цієї точки, який належить області визначення функції, і для всіх  з цього околу виконується нерівність
з цього околу виконується нерівність  (або
(або  ).
). ;
; .
. .
. .
. .
. існує для всіх
існує для всіх  .
. :
:
 похідна змінює знак з «+» на «-», отже
похідна змінює знак з «+» на «-», отже  похідна змінює знак з «-» на «+», тому
похідна змінює знак з «-» на «+», тому  .
. 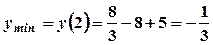 .
. .
. .
. або
або  , звідки
, звідки 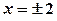 .
.
 ;
;  .
. .
. .
. .
. , звідки
, звідки  .
.
 похідна змінює знак з «-» на «+». Отже, точки
похідна змінює знак з «-» на «+». Отже, точки  похідна змінює знак, але
похідна змінює знак, але  , тому
, тому  парна, то
парна, то 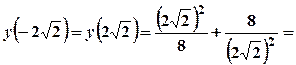
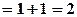 . Тобто
. Тобто  .
. .
. .
. .
. приймає тільки додатні значення, причому
приймає тільки додатні значення, причому  . Критичну точку знайдемо з умови:
. Критичну точку знайдемо з умови:  . Отримаємо
. Отримаємо 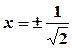 .
. .
.
 - точка мінімуму;
- точка мінімуму;  -точка максимуму.
-точка максимуму.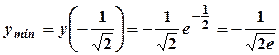 ;
; 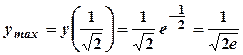 .
. .
.
 .
. .
. .
.
 похідна змінює знак з «+» на «-», тому
похідна змінює знак з «+» на «-», тому  похідна не змінює свій знак. Отже, критична точка
похідна не змінює свій знак. Отже, критична точка  .
. .
. .
. , тоді
, тоді  , звідки
, звідки  або
або  .
.
 .
. .
. .
. .
. , звідки
, звідки  . Але
. Але  не входить в
не входить в 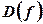 .
. При переході через точку
При переході через точку  .
. .
. .
. . Знайдемо
. Знайдемо  , тому рівняння не має коренів, тобто
, тому рівняння не має коренів, тобто  .
. ;
; ;
; ;
; ;
; .
. при
при  має вертикальну асимптоту, якщо
має вертикальну асимптоту, якщо  або
або  ; при цьому точка
; при цьому точка  є точкою розриву II роду. Рівняння вертикальної асимптоти має вигляд
є точкою розриву II роду. Рівняння вертикальної асимптоти має вигляд  , де
, де  ,
,  , якщо ці границі існують і скінченні.
, якщо ці границі існують і скінченні.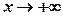 та
та  .
. .
. .
. функція має розрив II роду, тому що
функція має розрив II роду, тому що  .
. ,
,  .
. - похила асимптота.
- похила асимптота. .
.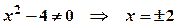 .
. .
. функція має розриви II роду, тому що
функція має розриви II роду, тому що  . Тому графік має дві вертикальні асимптоти
. Тому графік має дві вертикальні асимптоти 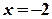 та
та  .
. ,
,  . Тоді
. Тоді  - горизонтальна асимптота.
- горизонтальна асимптота. .
.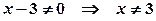 .
.
 , тому
, тому  - точка розриву II роду.
- точка розриву II роду. ,
, .
. - похила асимптота.
- похила асимптота. .
. .
. ,
,  .
. (коли
(коли  ) похилої асимптоти не існує. Знайдемо
) похилої асимптоти не існує. Знайдемо  . Щоб обчислити границю, перетворимо вираз
. Щоб обчислити границю, перетворимо вираз  до вигляду
до вигляду 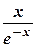 . Тоді маємо невизначеність
. Тоді маємо невизначеність  , до якої можна застосувати правило Лопіталя, а саме:
, до якої можна застосувати правило Лопіталя, а саме: 
 . Маємо:
. Маємо:  .
. .
.
 .
.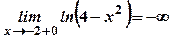 ,
, 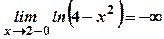 . В точках
. В точках  і
і 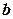 (функція не визначена при
(функція не визначена при  ).
). ;
; ;
; ;
; ;
; ;
; ;
; .
.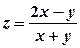 .
.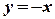 . Геометрично це означає, що область визначення функції складається із двох півплощин, одна з яких лежить вище, а друга нижче прямої
. Геометрично це означає, що область визначення функції складається із двох півплощин, одна з яких лежить вище, а друга нижче прямої 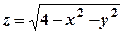 .
. , тобто
, тобто 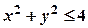 . Рівняння
. Рівняння  визначає в площині
визначає в площині 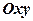 коло з центром в початку координат і радіусом
коло з центром в початку координат і радіусом 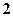 . Функція визначена в точках, які лежать усередині кола та на його межі, так як для всіх точок, які лежать поза колом, має місце нерівність
. Функція визначена в точках, які лежать усередині кола та на його межі, так як для всіх точок, які лежать поза колом, має місце нерівність  (рис.2.2).
(рис.2.2).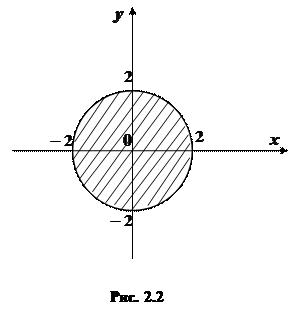
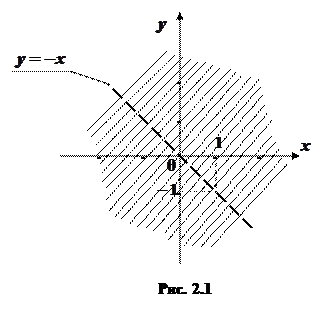
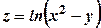 .
. Область визначення цієї функції визначається з нерівності
Область визначення цієї функції визначається з нерівності 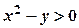 . Межа області – парабола
. Межа області – парабола  , яка ділить всю площину на дві частини. Щоб виявити, яка з частин є областю визначення даної функції, тобто задовольняє умову
, яка ділить всю площину на дві частини. Щоб виявити, яка з частин є областю визначення даної функції, тобто задовольняє умову 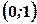 належить області визначення, тому що
належить області визначення, тому що 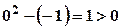 . Отже, область визначення даної функції є множина точок, розташованих нижче параболи. Межа (парабола
. Отже, область визначення даної функції є множина точок, розташованих нижче параболи. Межа (парабола 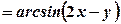 .
.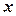 і
і 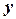 , які задовольняють нерівностям
, які задовольняють нерівностям 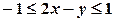 . На площині
. На площині 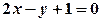 і
і  (рис.2.4)
(рис.2.4)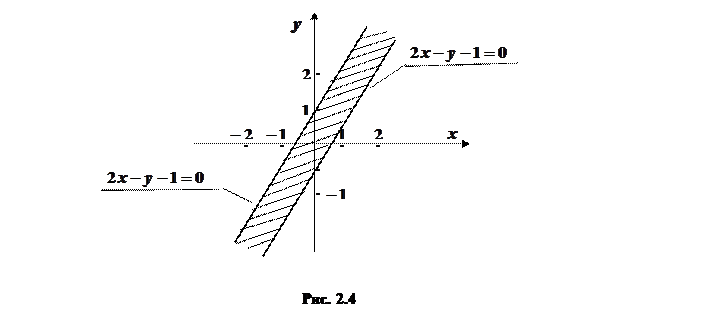
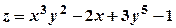 .
.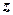 є функцією двох змінних
є функцією двох змінних  . Припускаючи, що стала
. Припускаючи, що стала 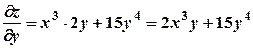 .
. .
.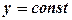 , маємо:
, маємо: 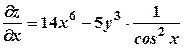 .
.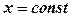 , то
, то 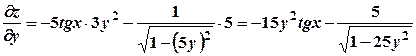 .
.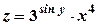 .
. ;
; 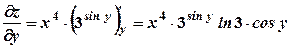 .
.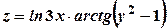 .
.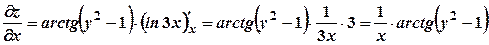 ;
;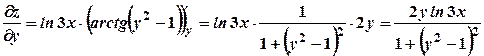 .
.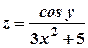 .
.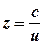 . Тому
. Тому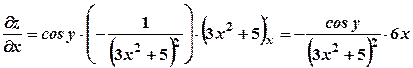 .
.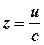 , тому
, тому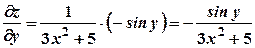 .
. .
.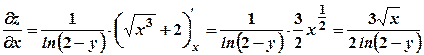 ;
;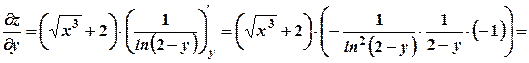
 .
.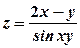 .
. і
і 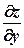 маємо функцію
маємо функцію  ;
;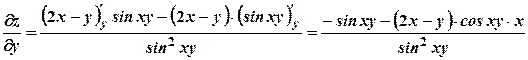 .
. .
.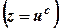 . Тоді отримаємо
. Тоді отримаємо  . При диференціюванні по
. При диференціюванні по 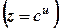 . Будемо мати
. Будемо мати  .
. .
.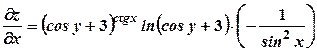 ;
; 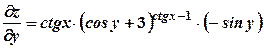 .
.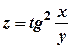 .
. і знаходимо частинну похідну від складеної функції по
і знаходимо частинну похідну від складеної функції по 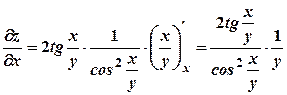 .
. .
.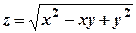 .
.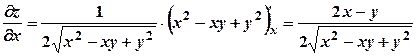 ;
;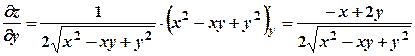 .
.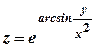 .
.
 ;
; 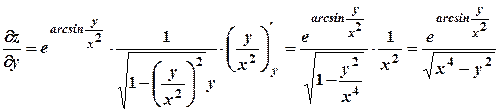 .
. .
.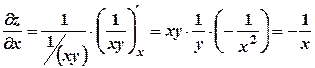 ;
;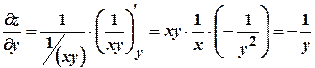 .
.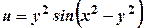 задовольняє рівняння
задовольняє рівняння 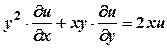 .
. :
: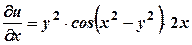 ;
;  .
.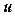 та її частинні похідні в наведене рівняння:
та її частинні похідні в наведене рівняння: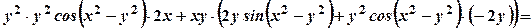
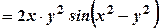 .
.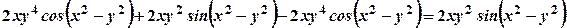 ;
;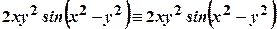 .
. ; б)
; б)  ; в)
; в)  ; г)
; г) 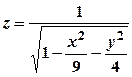 .
.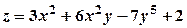 ;
;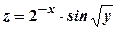 ;
; ;
;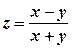 ;
;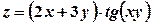 ;
;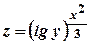 ;
; ;
;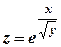 .
.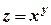 задовольняє рівняння
задовольняє рівняння 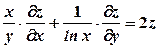 .
. .
. ;
;  .
. .
. .
. ;
;  .
. .
. .
. ;
;  . Будемо мати:
. Будемо мати:  .
. .
. ;
; .
. .
. .
. , тоді
, тоді  ;
;  . Покладемо, що
. Покладемо, що  ,
,  , обчислимо
, обчислимо  ,
,  . Тоді
. Тоді  . Знаходимо частинні похідні і їх значення в точці
. Знаходимо частинні похідні і їх значення в точці  , а саме
, а саме , тоді
, тоді  ;
; , тоді
, тоді  .
. .
. , а саме:
, а саме:  .
. , якщо
, якщо 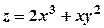 ,
,  ,
,  .
.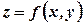 є складеною функцією змінної
є складеною функцією змінної  , тому за формулою (2.4) отримаємо:
, тому за формулою (2.4) отримаємо:  .
. ,
,  ,
,  ,
,  .
. .
. .
. , якщо
, якщо  ,
,  ,
,  .
. є складеною функцією змінної
є складеною функцією змінної  .
. ,
,  ,
,  ,
,  .
.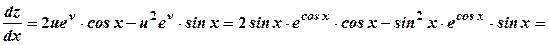
 .
. ,
,  .
. . Обчислимо:
. Обчислимо: ,
, ,
, .
. .
.
 .
. і
і  , якщо
, якщо  ,
,  ,
,  .
. . Для обчислення її похідних застосуємо формули (2.6).
. Для обчислення її похідних застосуємо формули (2.6). ,
, 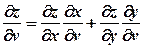 .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
, .
.
 ,
,
 .
. ,
,  ,
, 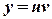 .
. - складена функція змінних
- складена функція змінних  ,
,  ,
, 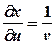 ,
,  ,
,  ,
,  .
.
 ,
, .
. ;
; ;
; .
.


