
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зростання і спадання функціїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функція Функція Як зростаючі, так і спадні функції називаються монотонними, а інтервали, в яких функція зростає або спадає – інтервалами монотонності. Зростання і спадання функції Інтервали монотонності можуть відділятися один від одного або точками, де похідна дорівнює нулю, або точками, де похідна не існує. Ці точки називаються критичними точками. Отже, щоб знайти інтервали монотонності функції 1) знайти область визначення функції; 2) знайти похідну даної функції; 3) знайти критичні точки з рівняння 4) розділити критичними точками область визначення на інтервали і у кожному з них визначити знак похідної. На інтервалах, де похідна додатна, функція зростає, а де від’ємна – спадає. Зразки розв’язування задач Знайти інтервали монотонності функції. 1. 1) Область визначення 2) 3) Критичні точки:
Похідна існує на всій області визначення. 4) Знаки похідної:
Функція зростає на інтервалах
2. 1) Область визначення 2) 3) Критичні точки: 4) 3. 1) Область визначення 2) 3) Критичні точки:
Похідна не існує в точці 4) На всій області визначення
4. 1) Область визначення 2) 3) Критичні точки:
Похідна існує на всій області визначення. 4) Знаки
Функція зростає на інтервалі 5. 1) Область визначення 2) 3) Критичні точки:
Похідна існує для всіх 4) Знаки похідної:
Функція зростає на інтервалі
6. 1) Функція визначена на множині дійсних чисел, крім точок 2) 3) Критичні точки:
Похідна існує на всій області визначення. 4) Знаки
Так як
Завдання для самостійної роботи Знайти інтервали монотонності функцій:
1.
2.
3.
4.
Локальний екстремум функції Точка Правило знаходження екстремумів (максимумів і мінімумів) за допомогою першої похідної: 1) знайти область визначення 2) знайти похідну 3) знайти критичні точки; 4) дослідити знак При цьому критична точка 5) обчислити значення функції в точках екстремуму (екстремуми).
Зразки розв’язування задач Знайти екстремуми функцій. 1. 1) Область визначення 2) 3) Критичні точки:
4) Знаки
При переході через точку 5) 2. 1) Область визначення функції 2) 3) Критичні точки:
4) Знаки
При переході через точку 5) 3. 1) Область визначення 2)
3) Критичні точки:
4) Знаки
При переході через точки 5) Так як функція
4. 1) 2) 3) Критичні точки:
Функція
4) Знаки
Функція має дві екстремальні точки:
5)
5. 1) Область визначення 2)
3) Критичні точки: а) б) 4) Знаки
При переході через точку 5)
6. 1) 2) 3) Критичні точки: а) б) 4)Знаки
При переході через точку
5) 7. 1) Область визначення 2) 3) Критичні точки: а) б) 4) Знаки
5)
8. 1) Область визначення 2) 3) Критичні точки: а) б) Отже, критичних точок не має і функція не має екстремумів.
Завдання для самостійної роботи Знайти екстремуми функцій: 1.
2.
3. 4.
5.
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.28.213 (0.009 с.) |

 називається зростаючою на інтервалі
називається зростаючою на інтервалі 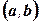 , якщо для будь-яких
, якщо для будь-яких 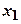 і
і 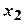 , що належать до цього інтервалу, і таких, що
, що належать до цього інтервалу, і таких, що 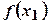 <
<  .
.
 >
>  , то функція зростає в цьому інтервалі; якщо ж
, то функція зростає в цьому інтервалі; якщо ж  , треба:
, треба: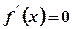 та за умови, що
та за умови, що 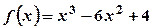 .
.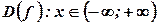 .
.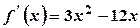 .
.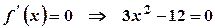 або
або  , звідки
, звідки 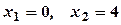 .
.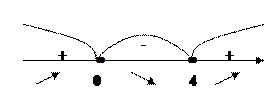
 і
і 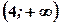 . Функція спадає на інтервалі
. Функція спадає на інтервалі 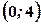 .
.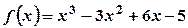 .
. .
.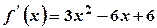 .
.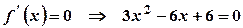 або
або 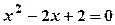 . Оскільки
. Оскільки 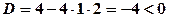 , рівняння не має коренів, тобто похідна не обертається в нуль.
, рівняння не має коренів, тобто похідна не обертається в нуль.  існує на всій області визначення. Отже, критичних точок немає.
існує на всій області визначення. Отже, критичних точок немає.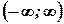 .
. .
. .
.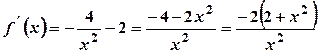 .
. , бо
, бо 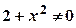 .
. , але ця точка не входить в
, але ця точка не входить в 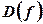 . Тобто критичних точок немає.
. Тобто критичних точок немає. , отже функція всюди спадає.
, отже функція всюди спадає.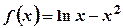 .
.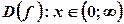 .
.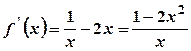 .
.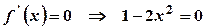 , звідки
, звідки 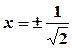 , але
, але 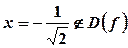 .
. :
: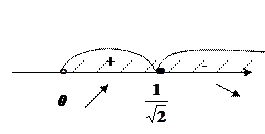
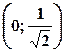 , спадає на інтервалі
, спадає на інтервалі 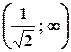 .
.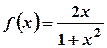 .
.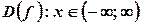 .
.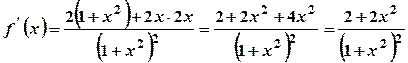 .
.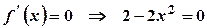 або
або 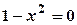 , звідки
, звідки  .
. .
.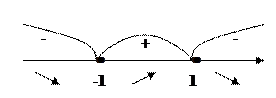
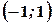 , спадає на інтервалах
, спадає на інтервалах 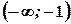 і
і 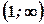 .
.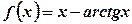 .
.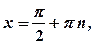
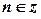 .
.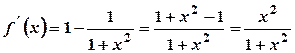 .
.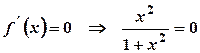 , звідки
, звідки 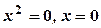 .
.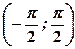 .
.
 на інтервалах
на інтервалах 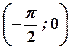 та
та  , і
, і  визначена в точці
визначена в точці 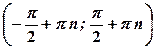 ,
, 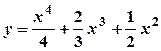 ;
;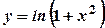 ;
;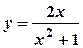 ;
;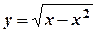 .
. називається точкою максимуму (або мінімуму) функції
називається точкою максимуму (або мінімуму) функції 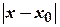 <
<  цієї точки, який належить області визначення функції, і для всіх
цієї точки, який належить області визначення функції, і для всіх  з цього околу виконується нерівність
з цього околу виконується нерівність  (або
(або  ).
). .
. .
. .
. :
:
 похідна змінює знак з «+» на «-», отже
похідна змінює знак з «+» на «-», отже  похідна змінює знак з «-» на «+», тому
похідна змінює знак з «-» на «+», тому  .
. 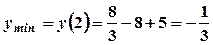 .
. .
. .
. або
або  , звідки
, звідки 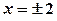 .
.
 ;
;  .
. .
. .
. , звідки
, звідки  .
.
 похідна змінює знак з «-» на «+». Отже, точки
похідна змінює знак з «-» на «+». Отже, точки  , тому
, тому 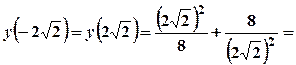
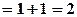 . Тобто
. Тобто  .
. .
. .
. .
. приймає тільки додатні значення, причому
приймає тільки додатні значення, причому  . Критичну точку знайдемо з умови:
. Критичну точку знайдемо з умови:  . Отримаємо
. Отримаємо  .
.
 - точка мінімуму;
- точка мінімуму;  -точка максимуму.
-точка максимуму.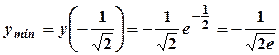 ;
; 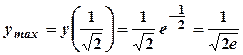 .
. .
.
 .
. .
. .
.
 похідна змінює знак з «+» на «-», тому
похідна змінює знак з «+» на «-», тому  похідна не змінює свій знак. Отже, критична точка
похідна не змінює свій знак. Отже, критична точка  .
. .
. .
. , тоді
, тоді  , звідки
, звідки  або
або  .
.
 .
. .
. .
. .
. , звідки
, звідки  не входить в
не входить в  При переході через точку
При переході через точку  .
. .
. .
. . Знайдемо
. Знайдемо  , тому рівняння не має коренів, тобто
, тому рівняння не має коренів, тобто  .
. ;
; ;
; ;
; ;
; .
.


