
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні відомості про найбільшеі найменше значення функції на проміжкуСодержание книги
Поиск на нашем сайте
Найбільше і найменше значення монотонної функції 1. Зайти критичні точки функції. 2. Знайти значення функції в критичних точках, які належать відрізку, і на кінцях відрізку. Найбільше і найменше значення з цих чисел і будуть відповідно найбільшим і найменшим значення функції на відрізку.
Задача № 1. Знайти найбільше і найменше значення функції:
Теоретичні відомості про екстремум функції
Теорема (друге правило). Якщо в точці
Задача №2. Знайти максимум і мінімум функції
Задача №3. Знайти довжини сторін прямокутника з периметром 72 см, що має найбільшу площу.
1. Фізичний зміст похідної. При прямолінійному русі точки швидкість в даний момент Прискорення 2. Геометричний зміст похідної. Похідна Задача №4. Знайти швидкість і прискорення точки, що рухається за законом Задача №5. Скласти рівняння дотичної до графіка функції
1. Які точки називаються критичними? 2. Правило знаходження найбільшого та найменшого значення функції. 3. Які точки називаються точками максимуму і точками мінімуму? 4. Перше правило відшукання екстремуму функції. 5. Друге правило відшукання екстремуму функції. 6. Фізичний зміст похідної. 7. Геометричний зміст похідної. Рівняння дотичної до графіка функції. Висновок __________________________________________________________ ____________________________________________________________________________________________________________________________________
Перевірив викладач_________________ Оцінка _________Дата________
ТЕМА 5. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
ПРАКТИЧНА РОБОТА № 11 Тема. Основні поняття та означення функції багатьох змінних. Частинні похідні. Екстремуми функції багатьох змінних. Необхідна умова існування точок екстремуму.
Мета роботи: засвоїтиозначення функції двох змінних, правила дослідження на екстремум; навчитись проводити дослідження функції двох змінних на екстремум; застосовувати здобуті навички для розв’язування прикладних задач економічного змісту.
Наочне забезпечення та обладнання: 1. Інструкційні картки; 2. Приклади задач; 3. Роздаткові матеріали: опорні конспекти “ Диференціювання функцій багатьох змінних” 4. Обчислювальні засоби: калькулятор.
Теоретичні відомості про правила диференціювання. Функцією двох змінних Аналогічно означається функція трьох і більше невідомих. Частинні похідні.
Частинні похідні функції знаходять за звичайними правилами диференціювання; потрібно тільки при диференціюванні по Якщо
Якщо мішані похідні неперервні, то вони рівні. Задача №1. Знайти частинні похідні першого і другого порядків від заданих функцій: а) z = 8e
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.9.174 (0.011 с.) |

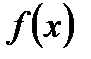 на відрізку
на відрізку 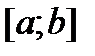 знаходиться на кінцях відрізка. Якщо ж задана функція не являється монотонною на відрізку
знаходиться на кінцях відрізка. Якщо ж задана функція не являється монотонною на відрізку 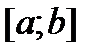 , але відомо, що вона неперервна, то для знаходження найбільшого і найменшого значення функції на відрізку необхідно:
, але відомо, що вона неперервна, то для знаходження найбільшого і найменшого значення функції на відрізку необхідно:

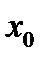 похідна
похідна 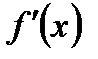 функції
функції 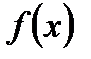 дорівнює нулю, а її друга похідна
дорівнює нулю, а її друга похідна  неперервна в околі цієї точки і
неперервна в околі цієї точки і 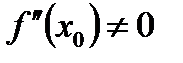 , то функція
, то функція 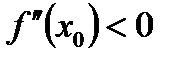 і мінімум, коли
і мінімум, коли  .
.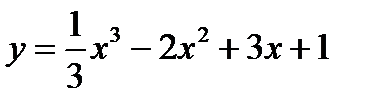
 дорівнює похідній
дорівнює похідній  від шляху
від шляху  по часу
по часу 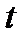 , обчисленій при
, обчисленій при 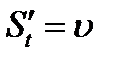 .
.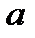 в даний момент
в даний момент  від швидкості
від швидкості 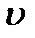 по часу
по часу 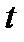 , обчисленій при
, обчисленій при  .
.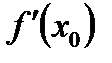 дорівнює кутовому коефіцієнту
дорівнює кутовому коефіцієнту  дотичної до кривої, проведеної у точці
дотичної до кривої, проведеної у точці 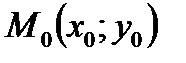 . Рівняння дотичної до графіка функції
. Рівняння дотичної до графіка функції 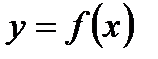 в точці з абсцисою
в точці з абсцисою 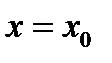 має вигляд:
має вигляд:  .
.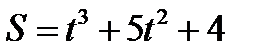 в момент часу
в момент часу 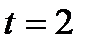 .
. в точці з абсцисою
в точці з абсцисою 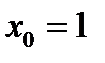 .
. Питання для самоконтролю знань, умінь
Питання для самоконтролю знань, умінь ,
,  називається функція, яка кожній парі чисел
називається функція, яка кожній парі чисел 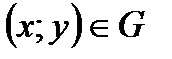 ставить у відповідність деяке число
ставить у відповідність деяке число 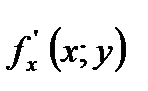 - це похідна по
- це похідна по 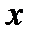 функції
функції 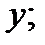
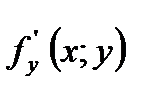 - це похідна по
- це похідна по 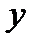 функції
функції 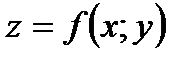 , то
, то 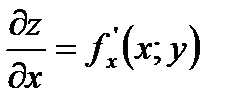 ;
; 
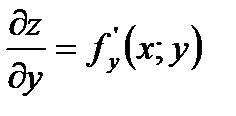 - частинні похідні першого порядку.
- частинні похідні першого порядку.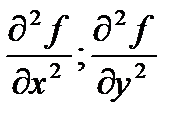 - частина похідної другого порядку.
- частина похідної другого порядку. - мішані похідні другого порядку.
- мішані похідні другого порядку. - 3xy
- 3xy 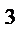 + 7x – 3
+ 7x – 3


