
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні відомості про диференціальні рівняння другого порядку зі сталими коефіцієнтамиСодержание книги
Поиск на нашем сайте 1. Лінійне однорідне диференціальне рівняння надалі (ЛОДР) другого порядку зі сталими коефіцієнтами має вигляд:
Функція де
Дане рівняння називають характеристичним рівнянням ЛОДР. 2. Якщо характеристичне рівняння (2) має два дійсні розв’язки
3. Якщо характеристичне рівняння (2) має один дійсний корінь k (в такому випадку кажуть, що воно має два дійсні корені, рівні між собою), то загальний розв’язок цього ЛОДР буде:
4. Якщо характеристичне рівняння (2) не має дійсних коренів, то воно має два спряжені комплексні корені
Задача 1. Знайти загальний розв’язок диференціального рівняння
Задача 2. Знайти загальний розв’язок диференціального рівняння
Задача3. Дано диференціальне рівняння а) загальний розв’язок рівняння; б) частковий розв’язок, що задовольняє початкові умови: y(0)=0 та
1. Загальний вигляд лінійного диференціального рівняння другого порядку з сталими коефіцієнтами. 2. Зміст характеристичного рівняння. 3. Випадки загального розв’язку диференціального рівняння з сталими коефіцієнтами в залежності від значення 4. Задача Коші для диференціальних рівнянь другого порядку з сталими коефіцієнтами.
Висновок.______________________________________________________________________________________________________________________________________________________________________________________________
Перевірив викладач ___________ Оцінка ___________ Дата___________
|

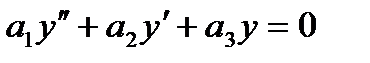 (1)
(1)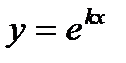 є розв’язком даного рівняння
є розв’язком даного рівняння  ,
,  ,
,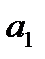 ;
;  ;
;  - сталі, причому
- сталі, причому 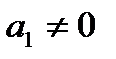 .
. 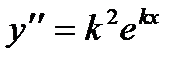 , підставивши значення
, підставивши значення  ,
, 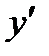 ,
,  в рівняння (1), одержимо:
в рівняння (1), одержимо: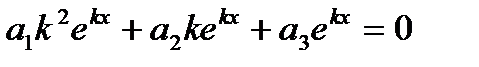 |:
|: 
 (2)
(2) , то загальний розв’язок ЛОДР (1) буде:
, то загальний розв’язок ЛОДР (1) буде: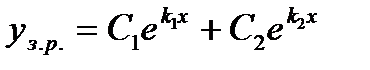 (3)
(3) .
. ,
,  , де а, b – дійсні числа, і – уявна одиниця (і
, де а, b – дійсні числа, і – уявна одиниця (і  ). Тоді загальним розв’язком ЛОДР (1) буде:
). Тоді загальним розв’язком ЛОДР (1) буде: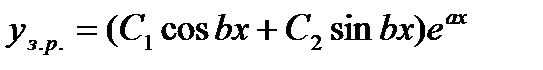
 .
.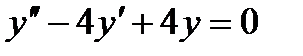 .
.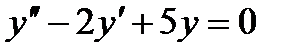 . Знайти:
. Знайти: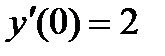 .
. Питання для самоконтролю знань, умінь
Питання для самоконтролю знань, умінь



