
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні відомості про визначники та їх властивостіСодержание книги
Поиск на нашем сайте
Розглянемо спочатку системи рівнянь, в яких кількість невідомих і кількість рівнянь рівні між собою, тобто m = n. Нехай, наприклад, n = m = 2, тоді маємо систему двох лінійних рівнянь з двома невідомими:
Визначникомдругого порядку називається вираз
Визначником третього порядку називається вираз:
Задача 1. Обчислити визначники, використовуючи: a) правило трикутників; б) метод розкладу за елементами першого рядка; в) правило Саррюса
Теоретичні відомості про матриці та дії над ними Означення. Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпців. Якщо повернутися до системи рівнянь (1.1), то коефіцієнти при невідомих у лівій частині якраз і утворюють таку прямокутну таблицю:
Сумою матриць одного й того самого порядку 2. Добутком матриці 3.Добутком матриці
Кожний елемент матриці С утворюється як сума добутків відповідних елементів і -го рядка матриці А на відповідні елементи Задача 2. Знайти
Задача 3. Розв’язати рівняння:
Задача 4. Знайти матрицю
Висновок _________________________________________________________ ____________________________________________________________________________________________________________________________________
Перевірив викладач ___________ Оцінка___________Дата ______________ ПРАКТИЧНА РОБОТА № 2 Тема. Розв’язування систем лінійних рівнянь основними методами: методом Гауса, за формулами Крамера Мета роботи: навчитись розв’язувати системи лінійних рівнянь методами Крамера та Гауса. Наочне забезпечення та обладнання: 1. Інструкційні картки; 2. Індивідуальні завдання; 3. Обчислювальні засоби.
Теоретичні відомості про правило Крамера Розглянемо систему n лінійних рівнянь з n невідомими:
Теорема. Якщо головний визначник
де
Задача 1. Розв’язати систему лінійних рівнянь за правилом Крамера: a)
|


 .
.
 .
.

 .
.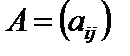 і
і  називається матриця
називається матриця 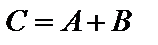 ;
; 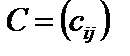 ,будь-який елемент якої дорівнює сумі відповідних елементів матриць А і В:
,будь-який елемент якої дорівнює сумі відповідних елементів матриць А і В:  .
. на деяке число
на деяке число  називається така матриця С, кожен елемент якої
називається така матриця С, кожен елемент якої  утворюється множенням відповідних елементів матриці А на
утворюється множенням відповідних елементів матриці А на  ,
,  .
.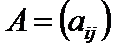 розміру
розміру  на матрицю
на матрицю 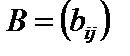 розміру
розміру  називається така матриця
називається така матриця  розміру
розміру 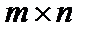 ,
, 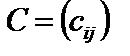 , кожний елемент можна знайти за формулою:
, кожний елемент можна знайти за формулою: .
. , якщо А=
, якщо А=  ,
, 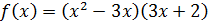
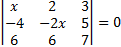
 ,
,  , якщо
, якщо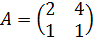 ,
, 
 Питання для самоперевірки знань, умінь
Питання для самоперевірки знань, умінь (1.4)
(1.4) складений із коефіцієнтів при невідомих системи n лінійних рівнянь з n невідомими (1.4), відмінний від нуля, то така система рівнянь має єдиний розв’язок (сумісна і визначена), який обчислюється за формулами:
складений із коефіцієнтів при невідомих системи n лінійних рівнянь з n невідомими (1.4), відмінний від нуля, то така система рівнянь має єдиний розв’язок (сумісна і визначена), який обчислюється за формулами: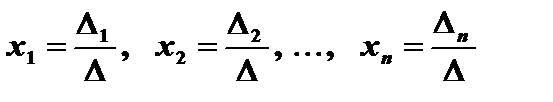 ,
, — головний визначник системи, який утворюється з коефіцієнтів при невідомих у лівій частині системи (1.4);
— головний визначник системи, який утворюється з коефіцієнтів при невідомих у лівій частині системи (1.4);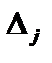 — визначник, який утворюється заміною j -го стовпця в головному визначнику на стовпець вільних членів.
— визначник, який утворюється заміною j -го стовпця в головному визначнику на стовпець вільних членів.



