
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні відомості про Метод Гауса розв’язування систем лінійних рівняньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод Гауса називають ще методом послідовного виключення невідомих. Він полягає в наступному: систему рівнянь приводять до рівносильної їй системі з трикутною матрицею (системи називаються рівносильними, якщо множини їх розв’язків співпадають). Дані дії називаються прямим ходом. З одержаної системи невідомі знаходять за допомогою послідовних підстановок, які називають зворотнім ходом. При виконанні прямого ходу використовують наступні перетворення: 1. множення або ділення коефіцієнтів вільних членів на одне і теж число; 2. додавання або віднімання рівнянь; 3. перестановка рівнянь системи; 4. виключення з системи рівнянь, в яких всі коефіцієнти при невідомих дорівнюють нулю. Універсальність методу Гауса полягає в тому, що за допомогою нього можна розв’язати систему будь-якого порядку. Продемонструємо розв’язування системи лінійних рівнянь методом Гауса на загальному прикладі. Розв’яжемо систему лінійних рівнянь:
Систему лінійних рівнянь (1) можна записати у вигляді розширеної матриці:
1) Прямий хід: розширену матрицю (2) шляхом послідовного виконання лінійних операцій над її рядками (тобто послідовного виконання операції додавання до одного рядка матриці іншого, помноженого на певне число) приводять до вигляду:
2) Зворотній хід: від розширеної матриці (3) переходять до відповідної системи рівнянь:
Останнє рівняння системи (4) дає значення змінної Задача 2. Розв’язати систему лінійних рівнянь методом Гауса: a)
1. Визначники матриць другого та вищих порядків. 2. Поняття системи n лінійних рівнянь відносно n невідомих. 3.Формули Крамера. Суть методу Крамера розв’язування систем лінійних рівнянь, його недоліки.
Висновок____________________________________________________________________________________________________________________________ __________________________________________________________________ Перевірив викладач ___________ Оцінка___________Дата ______________ ПРАКТИЧНА РОБОТА № 3 Тема. Розв’язування систем лінійних рівнянь матричним методом Мета роботи: навчитись розв’язувати системи лінійних рівнянь за допомогою оберненої матриці (матричним методом). Наочне забезпечення та обладнання: 1. Інструкційні картки; 2. Індивідуальні завдання; 3. Обчислювальні засоби.
Нехай дано систему n лінійних рівнянь з n невідомими
Запишемо дану систему у вигляді матричної рівності:
де
Тобто:
Розв’язати систему (1) означає знайти такі значення невідомих Систему лінійних рівнянь називають не виродженою, якщо матриця системи не вироджена, тобто detA≠0. Невироджена система лінійних рівнянь має єдиний розв’язок. Розв’язок невиродженої системи лінійних рівнянь, записаної у вигляді матричного рівняння знаходять за формулою:
Задача. Розв’язати систему лінійних рівнянь матричним способом: a)
|

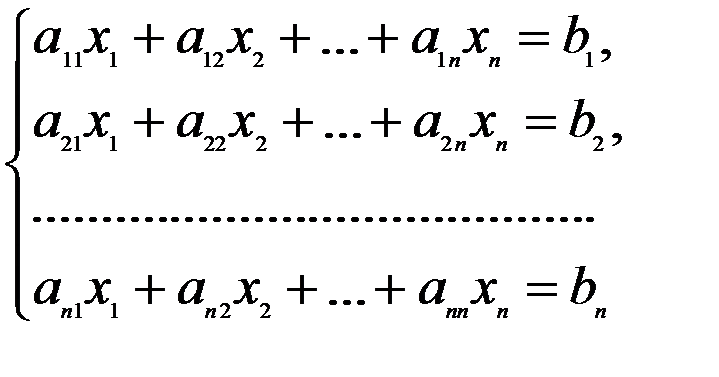 (1)
(1) (2)
(2) (3)
(3) (4)
(4)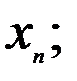 підставляючи це значення в передостаннє рівняння знаходимо змінну
підставляючи це значення в передостаннє рівняння знаходимо змінну  продовжуючи цей процес, поступово знаходимо значення всіх невідомих.
продовжуючи цей процес, поступово знаходимо значення всіх невідомих.
 Питання для самоперевірки знань, умінь
Питання для самоперевірки знань, умінь Теоретичні відомості про матричний спосіб розв’язування систем лінійних рівнянь
Теоретичні відомості про матричний спосіб розв’язування систем лінійних рівнянь (2)
(2) - квадратна матриця n-го порядку, складену з коефіцієнтів при невідомих (її називають матрицею системи);
- квадратна матриця n-го порядку, складену з коефіцієнтів при невідомих (її називають матрицею системи); матриця розмірності (n×1), складена з невідомих;
матриця розмірності (n×1), складена з невідомих; матриця розмірності (n×1), складена з вільних членів.
матриця розмірності (n×1), складена з вільних членів.


 які перетворюють в істинні рівності одночасно всі рівняння системи. Це теж саме, що знайти невідому матрицю
які перетворюють в істинні рівності одночасно всі рівняння системи. Це теж саме, що знайти невідому матрицю  , яка перетворює в істинну рівність матричне рівняння (2).
, яка перетворює в істинну рівність матричне рівняння (2). де
де  - матриця, обернена до матриці
- матриця, обернена до матриці 



