
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зв’язок між розв’язками неоднорідних і однорідних систем.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай дана система лінійних неоднорідних рівнянь
Система лінійних однорідних рівнянь
яка одержується з системи (2) заміною вільних членів нулями, називається зведеною системою для системи (2). Зв’язок між розв’язками систем (2) і (3): 1. Сума будь-якого розв’язку системи (2) з будь-яким розв’язком зведеної системи (3) знову буде розв’язком системи (2). 2. Різниця будь-яких двох розв’язків системи (2) є розв’язком для зведеної системи (3). Наслідок. Знайшовши один розв’язок системи лінійних неоднорідних рівнянь (2) і додавши до нього кожний з розв’язків зведеної системи (3), ми одержимо всі розв’язки системи (2). Приклад. Знайти загальний та один частинний розв’язок системи лінійних рівнянь:
Знайдемо загальний розв’язок відповідної однорідної системи рівнянь.
Загальний розв’язок СЛОР (-1/4x4-13/4x5, -3/4x4-11/4x5, 0,x4,x5), x4,x5 є R. Частинний розв’язок СЛР (1,1,0,0,0). Загальний розв’язок СЛР (1-1/4x4-13/4x5, 1-3/4x4-11/4x5, 0,x4,x5), x4,x5 є R.
Лінійний многовид. Означення. Нехай V¢ – підпростір лінійного простору V, а х0 – деякий вектор з V. Множина Р всіх векторів х=х0+y, де y – будь-який вектор підпростору V¢, називається лінійним многовидом простору V. Лінійний многовид Р утворюється шляхом зсуву підпростору V¢ на вектор х. Означення. Розмірністю многовиду Р називається розмірність того підпростору V¢, зсувом якого було одержано цей многовид. Теорема 8. Множина розв’язків СЛР є лінійним многовидом, одержаним шляхом зсуву підпростору V¢ розв’язків відповідної СЛОР на вектор х0, де х0 – один довільно вибраний і фіксований розв’язок СЛР. "х є Р (Р=х0+V={x0+aïa є V}) Приклад. Побудувати лінійний многовид Р розв’язків такої СЛР:
Загальний розв’язок СЛР (х1,х2,-3х1-4х2+1,1). Загальний розв’язок СЛОР (х1,х2,-3х1-4х2,0).
L¢((1,0,-3,0),(0,1,-4,0)), Р=(0,0,1,1)+L¢((1,0,-3,0),(0,1,-4,0)).
Розділ 2. Матриці та дії над матрицями. Матриці. Означення. Матрицею називається прямокутна таблиця, яка складається з елементів даного поля. Загальний вигляд матриці: A = де аij,аi ,bj - елементи матриці. Якщо в матриці А кількість рядків дорівнює кількості стовпців, тобто m=n, то вона називається квадратною матрицею n-го порядку; якщо ж m¹n, то матриця називається прямокутною матрицею розміру m*n. Головною діагоналлю квадратної матриці n-го порядку називається діагональ, яка йде від лівого верхнього кута до нижнього правого, тобто яка складається з елементів а11,а22,…,аnn.
Означення. Квадратна матриця D=(dij) n-го порядку називається діагональною, якщо всі її елементи, які не належать головній діагоналі, дорівнюють нулю: "i, j (i¹ j => dij=0). Елемент головної дігоналі матриці називають i-им дігональним елементом. Діагональна матриця називається скалярною, якщо елементи її головної діагоналі рівні між собою. Діагональна матриця: D = Скалярна матриця: K = Частинним випадком скалярної матриці є одинична E і нульова O: E = Дві матриці називаються рівними, якщо рівні відповідні їх елементи. Від матриці А можна перейти до матриці А¢: A¢ = в якій рядки є стовпцями, а стовпці – рядками матриці А. Перехід від матриці А до матриці A¢ називається транспонуванням матриці А, а матриця А¢ називається транспонованою для матриці А. Якщо матриця Якщо А – довільна квадратна матриця і A¢=A, то А називається симетричною; якщо A¢=-А, то А - кососиметрична. Квадратна матриця ортогональна, якщо АА¢=A¢A=E. Матриця називається ідемпотентною, якщо А2=А.
Дії з матрицями. Означення. Нехай дано матриці А=(аij)m*n, В=(bij)m*n над полем Р. Матриця (аij+bij)m*n називається сумою матриць А і В і позначається А+В; при цьому матриці А,В називаються доданками. Операція, яка матрицям А і В ставить у відповідність матрицю А+В називається сумою матриць. А+В=(аij+bij) Властивості додавання матриць: 1) Операція додавання матриць комутативна, тобто для А=(аij)m*n, В=(bij)m*n однакового розміру А+В=В+А; 2) Операція додавання матриць асоціативна, тобто А=(аij)m*n, В=(bij)m*n, С=(сij)m*n однакового розміру (А+В)+С=А+(В+С); 3) В множині матриць А даного розміру існує одна матриця О, яка є нейтральним елементом відносно операції додавання матриць, тобто така, що "А A+О=О+A=A, її називають нульовою матрицею; 4) В множині матриць даного розміру для кожної матриці А існує єдина протилежна матриця А¢¢, тобто така, що A+A¢¢=A+A¢¢=O.
Приклад. Дано матриці А і В. Знайти А+В і В+А і порівняти їх. A = A+B = B+A = Отже, А+В=В+А. Приклад. Дано матриці А і В. Знайти А+В. А = Сума матриць А+В, В+А не існує, оскільки матриці різної розмірності. Умови існування суми матриць: матриці повинні бути однакового розміру. Означення. Нехай дана матриця А=(аij)m*n над полем Р і елемент k є Р. Добутком матриці А на елемент k називається матриця (kаij)m*n, яка позначається kA. Властивості множення матриці на скаляр: 1) Операція множення матриці на скаляр асоціативна в тому розумінні, що для довільної матриці А і чисел k,l є Р: k(lA)=(kl)A=klA; 2)Операція множення матриці на скаляр дистрибутивна відносно додавання матриць і відносно додавання скалярів, тобто "A "k,l є Р (k+l)A=kA+lA "A,B "k є Р k(A+B)=kA+kB, де А і В однакового розміру. Приклад. Дано матриці А і В, скаляри k,l. Знайти (k+l)A,k(A+B). A = (k+m)A = (2-1) k(A+B) = 2 Означення. Дано матриці А=(аij)m*n і В=(bsk)n*l, які належать полю Р. Матриця (сpq)m*l, де сpq=ap1b1q+ap2b2q+…+apnbnq називається добутком матриці А на матрицю В і позначається АВ. При цьому матриця А називається лівим множником, матриця В – правим множником. Операція, яка матрицям А і В ставить у відповідність матрицю АВ, називається множенням матриць. Отже, АВ=(сpq), де сpq=ap1b1q+ap2b2q+…+apnbnq, тобто сpq є сумою добутків відповідних елементів р-го рядка і q-го стовпчика. Зауваження. Добуток мартиць існує тоді і лише тоді, коли кількість стовпчиків першої матриці дорівнює кількості рядків другої матриці. Властивості множення матриць: 1) Операція множення матриць в загальному випадку некомутативна. Але існують такі матриці А,В, що АВ=ВА. Наприклад, АЕ=ЕА=А, АО=ОА=О. Якщо матриці А і В задовольняють умову АВ=ВА, то такі матриці є перестановочними або комутативними. Комутативними є лише квадратні матриці. 2) Операція множення асоціативна, тобто "А,В,С (АВ)С=А(ВС) 3) Асоціативність множення матриці на матрицю і на скаляр "А,В "k,l є Р (kA)B=k(AB) A(kB)=(Ak)B=(kA)B 4) В множині квадратних матриці n-го порядку існує єдина матриця E, яка є нейтральним елементом відносно операції множення матриць, тобто така, що "А (AE=EA=A) Для множини прямокутних матриць А розміром m*n можна говорити про існування односторонніх нейтральних елементів, тобто таких матриць В і С, що "А (АВ=СА=А). Операції додавання і множення матриць А і В одночасно можна виконувати лише тоді, коли А і В – квадратні матриці одного порядку. В множині квадратних матриць n-го порядку мають місце дистрибутивні закони (правий і лівий) множення відносно додавання: "А,В,С- n-го порядку (А+В)С=АС+ВС С(А+В)=СА+СВ. З сказаного вище слідує, що множина всіх квадратних матриць n-го порядку над полем Р є кільцем з одиницею відносно операцій додавання і множення матриць (некомутативне кільце). Позначається Мn=<Mat
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.31 (0.009 с.) |

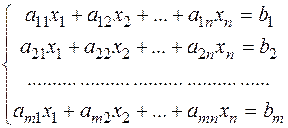 (2)
(2) (3)
(3)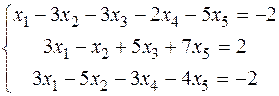




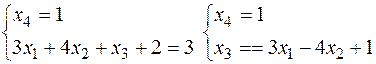
 = (аij), А = (a1,a2,…,an), В =
= (аij), А = (a1,a2,…,an), В = 


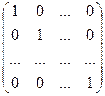 q =
q = 
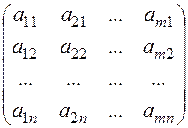
 B =
B = 


 B =
B = 
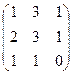 B =
B = 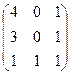 k=2, m=-1
k=2, m=-1
 +
+  = 2
= 2 
 (R),+,*>.
(R),+,*>.


