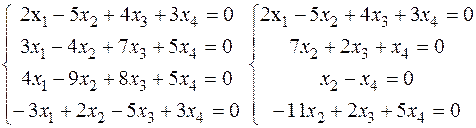Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійна залежність векторів.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Означення. Вектор b з простору Vn називається пропорційним вектору a з цього ж простору, якщо існує таке число k таке, що b=ka. Нульовий вектор q=(0,0,…,0) пропорційний будь-якому вектору а=(а1,а2,…,аn) тому, що q = 0*а. Нехай а1,а2,…,аm (1) довільна система векторів з простору. Означення. Вектор b є Vn називається лінійною комбінацією векторів а1,а2,…,аm, якщо існують такі числа k1,k2,…,km, що b=k1a1+k2a2+…+kmam (2) Числа k1,k2,…,kn називаються коефіцієнтами цієї лінійної комбінації. Нульовий вектор q=(0,0,…,0) є лінійною комбінацією векторів будь-якої системи, оскільки q=0*а1+0*а2+…+0*аm. Означення. Система векторів а1,а2,…,аm простору Vn називається лінійно залежною, якщо існують такі числа k1,k2,…,km не всі рівні нулю і k1a1 +k2a2+…+kmam=0. (*) Система векторів називається лінійно незалежною, якщо рівність (*)виконується лише при k1 = k2 = …= km = 0. Приклади. 1) З’ясувати лінійно залежною чи лінійно незалежною є система векторів a1=(1,-2,-3), а2=(2,3,4), а3=(3,5,7). Запишемо рівняння (*) k1a1+k2a2+k3a3=0. Звідси одержимо систему
Розв’яжемо її методом Гауса
Отже, система векторів є лінійно незалежною. 2)а1 = (1,2sinA,tgA,2cosA) a2 = (ctgA,2cosA,1,0) a3 = (cosA,sin2A,sinA,1+cos2A), a4 = (tgA,1,0,2sinA). Аналогічно попереднім міркуванням маємо:
k4 = 0, k2 = tgA/2/(1-2sinAtgA)k3 Отже, існує k2¹0, а рівняння (*) виконується. Отже, система лінійно залежна. Теорема 1. (ознака лінійної залежності системи) Система векторів (1) лінійно залежна тоді і тільки тоді, коли хоча б один з векторів цієї системи є лінійною комбінацією інших її векторів. Наслідок 1. Будь-яка система векторів, яка містить нульовий вектор, лінійно залежна. Наслідок 2. Якщо в системі є пропорційні (колінеарні) вектори, то система лінійно залежна. Теорема 2. Якщо система векторів а1,а2,…,аm лінійно незалежна, а система векторів а1,а2,…,аm,b лінійно залежна, то вектор b є лінійною комбінацією векторів а1,а2,…,аm. Означення. Множина, яка складається з будь-яких k (k£m) векторів системи (1) називається підсистемою цієї системи. Теорема 3. Якщо деяка підсистема системи векторів (1) лінійно залежна, то і система (1) лінійно залежна. Наслідок. Якщо система векторів (1) лінійно незалежна, то і будь-яка її підсистема теж лінійно незалежна. Теорема 4. Будь-які s векторів арифметичного n-мірного простору складають при s>n лінійно залежну систему.
§6. Базис і ранг скінченної системи векторів Нехай а1,а2,…,аm (3) –довільна система векторів простору Vn і аi1,аi2,…,аin (4) –деяка лінійно незалежна підсистема цієї системи. Означення. Лінійно незалежна підсистема (4) системи векторів (3) називається базисом системи (3), якщо кожний вектор системи (3) є лінійною комбінацією векторів цієї підсистеми. Теорема 6. Два різних базиса однієї і тієї ж системи векторів містять однакову кількість векторів. Наприклад за базис V3 можна взяти систему е1=(1,0,0), е2=(0,1,0), е3=(0,0,1) або а1=(1,2,-2), а2=(0,-1,3), а3=(0,-2,4). Але система b1=(1,-2,-3), b2=(1/2,-1,-3/2), b3=(4,5,6) не є базисом так, як вона містить пропорційні рядки, тобто є лінійно залежною. Означення. Кількість векторів, які входять в будь-який базис даної системи векторів, називається рангом цієї системи. Ранг системи векторів – це максимальне число лінійно незалежних векторів системи. Приклад. 1) Знайти один з базисів системи векторів і виразити всі її вектори, що не входять до знайденого базису, через цей базис: а1 = (4,1,2), а2 = (1,0,3), а3 = (2,3,-5), а4 = (1,1,6). Складемо матрицю, рядками якої є дані вектори і зведемо її до діагонального виду
При елементарних перетвореннях координати вектора а перетворилися в 0, тому базисом даної системи векторів є вектори а2,а3,а4. Виразимо вектор а1 через базис: а1=k1a2+k2a3+k3a4, де ki невідомі коефіцієнти. Складемо матрицю даного рівняння:
Одержимо систему Отже, а1=21/4a2+13/20a3-19/20a4. Іншим базисом даної системи векторів є вектори а1,а2,а3. Означення. Системою твірних називається система векторів а1,а2,…,аn множини векторів лінійного простору, якщо будь-який вектор з цієї множини можна лінійно виразити через скінченне число векторів а1,а2,…,аn: a1,а2,…,аn – система твірних º "аi (аi=k1a1+k2a2+…+knan). Ознака лінійної залежності системи векторів - cистема векторів лінійно залежна тоді і тільки тоді, коли знайдеться вектор в цій системі, який є лінійною комбінацією інших векторів цієї системи: a1,а2,…,аn – лінійно залежна ó $ai (ai=k1a1+k2a2+…+knan). Означення. Лінійно незалежна система твірних називається базисом векторного простору. Ознака базису: базис – максимально лінійно незалежна система векторів. Максимальна в тому розумінні, що якщо до неї приєднати ще один вектор, то вона стане лінійно залежною.
Теорема. Кількість векторів в довільному базисі скінченно вимірного простору є інваріантом цього простору (одна і та ж для простору), а розмірність простору дорівнює кількості векторів в базисі цього простору. Наприклад, система з 5 лінійно незалежних векторів утворює базис, а система з 6 векторів є лінійно залежною і базис на утворює.
§7. Однорідні системи лінійних рівнянь. Лінійне рівняння а1х1+а2х2+…+аnхn=b називається однорідним, якщо його вільний член b дорівнює нулю. Систему лінійних рівнянь, в якій всі вільні члени дорівнюють нулю, називають однорідною системою лінійних рівнянь (СЛОР). Загальний вигляд СЛОР:
Будь-яка однорідна лінійна система сумісна. Вона завжди має розв’язок х=(0,0,…,0)- нульовий (тривіальний) розв’язок. Будь-який розв’язок СЛОР, відмінний від нульового називають ненульовим (нетривіальним) розв’язком. Насправді, не будь-яка СЛОР має ненульові розв’язки. Теорема. (достатня умова існування ненульових розв’язків СЛОР) Однорідна система лінійних рівнянь, в якій кількість рівнянь менша кількості невідомих, має ненульові розв’язки. Розв’язки СЛОР мають такі властивості: 1) Якщо вектор b=(b1,b2,…,bn) є розв’язком системи (1), то при довільному числі k вектор kb=(kb1,kb2,…,kbn) також буде розв’язком цієї системи. 2) Будь-яка лінійна комбінація розв’язків однорідної системи (1) сама буде розв’язком цієї системи. Розглянемо множину L розв’язків СЛОР. Нехай а=(а1,а2,…,аn) і b=(b1,b2,…,bn) є розв’язками СЛОР. Покажемо, що множина розв’язків СЛОР утворює підпростір Vn, тобто, що виконуються такі умови: 1) a+b=(а1+b1,а2+b2,…,а3+bn); 2) ka=(kа1,kа2,…,kаn). Вектори a+b i ka є розв’зками СЛОР за властивістю розв’язків СЛОР. Отже, множина розв’язків СЛОР утворює підпростір Vn. У випадку неоднорідної системи така властивість місця не має. Теорема 7. (про розмірність простору розв’язків СЛОР) Розмірність простору розв’язків СЛОР дорівнює різниці кількості змінних n і рангу основної матриці системи r. dimL=n-r Означення. Будь-яка лінійно незалежна система векторів однорідної системи лінійних рівнянь, через яку лінійно виражається довільний розв’язок цієї системи, називається її фундаментальною системою розв’язків. Іншими словами базис простору розв’язків СЛОР називається фундаментальною системою розв’язків. Приклад. 1) Побудувати простір розв’язків СЛОР:
Загальний розв’язок системи х=(х4,х4,-х4,х4),х4 є R. Знайдемо фундаментальну систему розв’язків ФСР. Для цього вільним змінним надамо довільних значень. Зауважимо, що не можна всім вільним змінним одночасно надавати значення 0, бо нуль-вектор не може належати до базиса простору розв’язків СЛОР. Надамо змінній х4 значення 1, одержимо один вектор ФСР а=(1,1,-1,1). Знаючи базис простору розв’язків можна записати L={bïb=ka, k є R}. 2) Побудувати простір розв’язків СЛОР:
х1=х2=х3=х4=0. Так як розв’язком СЛОР є лише нульовий вектор, то ФСР не існує. 3) Побудувати простір розв’язків СЛОР:
Загальний розв’язок системи (8х3-7х4,-х3+5х4,х3,х4),х3,x4єR. Для знаходження базису простору складемо табличку
Фундаментальна система розв’язків: а1=(8,-6,1,0), а2=(-7,5,0,1). Знаючи базис простору розв’язків можна записати L={bïb=k1a1+k2a2, k1,k2 є R}.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.116.245 (0.012 с.) |


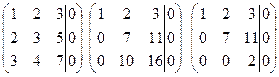
 => x1=x2=x3=0.
=> x1=x2=x3=0.




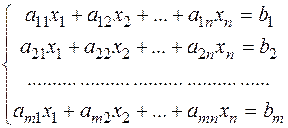 (1)
(1)