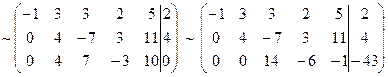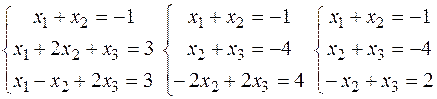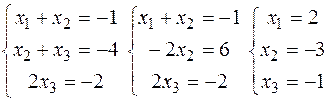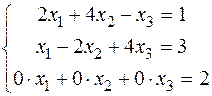Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття системи лінійних рівнянь і її розвязків.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лінійним рівнянням з n невідомими називається рівняння виду а1х1+а2х2+…+аnхn=b, (1), де х1,х2,…,хn - невідомі, а1,а2,…,аn - деякі числа з деякого числового поля Р. Числа а1,а2,…,аn називають коефіцієнтами рівняння (1), а число b - вільним членом цього рівняння. Рівняння виду 0*х1+0*х2+…+0*хn=0 називається невизначенним. Рівняння виду 0*х1+0*х2+…+0*хn =b, b¹0 називається суперечливим. Означення. Розв’язком рівняння (1) називається такий n-мірний числовий вектор а=(а1,а2,…,аn), що рівняння (1) перетворюється в істинну рівність після заміни в ньому невідомих хi відповідними координатами аi. Приклад. 1)3х1+4х2=13 – лінійне рівняння з двома невідомими, вектор а=(3,1) розв’язок даного рівняння. 2)3х1+4х2–5х3=0 – лінійне рівняння з трьома невідомими. Вектор а=(2,1,2) – розв’язок рівняння, вектори b=(1,3,3), 0=(0,0,0) також є розв’язками цього рівняння. Нехай дано m лінійних рівнянь з невідомими х1,х2,…,хn, які розглядаються над одним числовим полем Р, і стоїть задача знайти спільний розв’язок всіх рівнянь. В такому випадку кажуть, що задана система m лінійних рівнянь з n невідомими(СЛР) і її записують наступним чином:
де х1,х2,…,хn - невідомі, а11,а12,…,аmn і b1,b2,…,bm - деякі числа з поля Р. Числа а11,а12,…,аmn називаються коефіцієнтами системи, а числа b1,b2,…,bm – вільними членами системи. Коєфіцієнти, які стоять в системі (2) при невідомих хi і вільні члени цієї системи складають m-мірні числові вектори. Система (2) рівносильна рівнянню (3) х1а1+х2а2+…+хnаn=b. Рівняння (3) називають векторною формою системи лінійних рівнянь. Означення. Розв’язком системи лінійних рівнянь (2) називається будь-який n-мірний числовий вектор а=(а1,а2,…,аn), який є розв’язком кожного з рівнянь цієї системи. Система рівнянь, яка має хоча б один розв’язок, називається сумісною; система рівнянь, яка не має жодного розв’язку, називається несумісною. Якщо в системі зустрічається суперечливе рівняння, то система несумісна. Виключення з системи невизначеного рівняння не впливає на розв’язок системи. Теорема. Якщо система лінійних рівнянь має два різних розв’язки, то вона має їх безліч. Отже, сумісна система лінійних рівнянь може мати або один розв’язок, або безліч. Означення. Сумісна система лінійних рівнянь називається визначеною, якщо вона має єдиний розв’язок; вона називається невизначеною, якщо має безліч розв’язків.
Отже, якщо система має єдиний розв’язок, то вона є сумісновизначеною, кілька розв’язків - сумісно невизначена, жодного, то несумісна. Розв’язати СЛР - це означає дослідити, сумісна вона чи ні; у випадку сумісності встановити число її розв’язків і знайти їх. Матрицю, яка складена з коефіцієнтів СЛР (2) називають основною матрицею цієї системи, а матрицю, яка складена з коефіцієнтів і вільних членів системи, називають розширеною матрицею цієї системи. Системи лінійних рівнянь називають рівносильними, якщо множини їх розв’язків співпадають. Щоб розв’язати СЛР застосовують елементарні перетворення. 1) Дослідити на сумісність і визначеність СЛР:
Складаємо розширену матрицю цієї системи
1. Якщо k=1, то система несумісна; 2. Якщо k¹1, то
Загальний розв’язок (
Елементарні перетворення. Означення. Елементарними перетвореннями системи лінійних рівнянь називаються такі перетворення: 1) перестановка місцями (транспозиція) двох рівнянь системи; 2) множення будь-якого рівняння системи на число, відмінне від нуля; 3) додавання до одного рівняння системи іншого її рівняння, помножене на деяке число; 4) викреслення невизначеного рівняння. Теорема Гауса. Елементарні перетворення системи не змінюють множину її розв’язків, тобто приводять нас до рівносильної системи. Ідея метода Гауса СЛР полягає в тому, що за допомогою елементарних перетворень переходимо від даної системи до системи виду трикутника або трапеції і розв’язуємо одержану систему, а оскільки вона рівносильна даній, то одержуємо розв’язок (множину розв’язків) початкової системи. Алгоритм: 1) якщо в системі є суперечливе рівняння, то система несумісна; 2) якщо в системі є невизначене рівняння, то викреслюємо його; 3) робимо коефіцієнт а11¹0; 4) перше рівняння залишаємо, наступні рівняння утворюємо так: перше рівняння а11х1+а12х2+…+а1nхn=b1 домножуємо на –а1n/а11 і додаємо до наступних. В результаті одержимо систему:
Далі аналогічно беремо рівняння a22¢x2+…+a2n¢xn=b2¢ і обнуляємо коефіцієнти аk2¢, k³3. Отже, дану систему ми звели до діагонального виду
в якій діагональні елементи аii¹0(i=1,…,r,r<=k).
В результаті цих перетворень, якщо матриця СЛР зводиться: 1) до виду трикутника, то СЛР має єдиний розв’язок; 2) до виду трапеції, тоді СЛР має безліч розв’язків. Змінні, через які ми виражаємо всі інші змінні називаються вільними змінними. Для зручності обчислень будемо використовувати матриці, бо перетворення з рядками зводяться до переворень з коефіцієнтами. Приклад. 1) Розв’язати систему лінійних рівнянь методом Гауса:
Дана система звелась до виду трикутника. Її розв’язок (1,2,69/23). 2) Розв’язати систему лінійних рівнянь методом Гауса:
х1=-12-44 3/4x3+26 3/4x4, x2=-19-39 1/4x3+18 1/4x4, x3,x4 є R, x5=4+14x3-6x4. Cистема звелась до виду трапеції. Її розв’язок (-12-44 3/4x3+26 3/4x4, -19-39 1/4x3+18 1/4x4, x3,x4, 4+14x3-6x4), х3,x4 є R. 3) Розв’язати систему лінійних рівнянь методом Жордана-Гауса:
Отже її розв’язок (2,-3,-1). 4) Розв’язати систему лінійних рівнянь:
Дана система містить суперечливе рівняння, отже вона розв’язків немає.
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.243.30 (0.009 с.) |

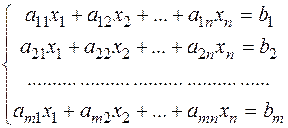 (2)
(2)
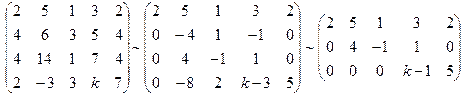
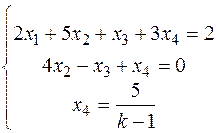
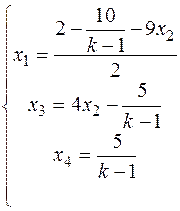
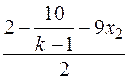 ,
, 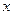
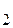 ,
, 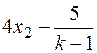 ,
, 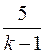 ).
).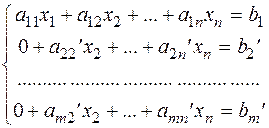
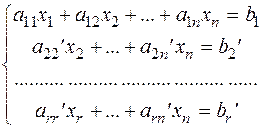
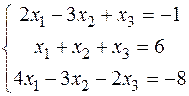
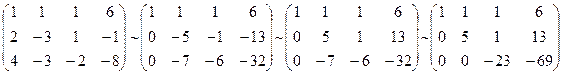

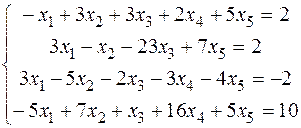
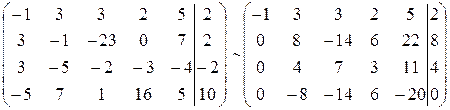 ~
~