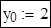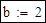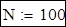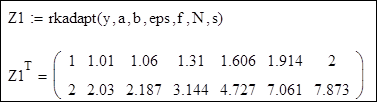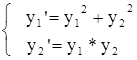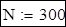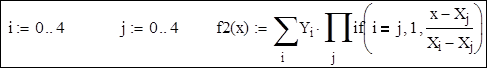Розв'язання нелінійних рівнянь

 

Постановка задачі

 

Будь-яке рівняння з одним невідомим може бути записане у вигляді

 

f(x) = 0.

 

Розв'язання даного рівняння полягає у знаходженні коренів, тобто тих значень х, що перетворюють рівняння в тотожність.

Завдання

Дано нелінійне рівняння

 

 

Необхідно:

1) побудувати графік функції y = f(x) і визначити наближені значення коренів рівняння за допомогою інструментів Trace і Zoom;

2) розв'язати рівняння за допомогою функції root;

3) розв'язати рівняння за допомогою функції polyroots;

4) розв'язати рівняння за допомогою розв'язувального блока Given... Find.

 

Порядок виконання

 

1.Графічне розв'язання за допомогою інструментів Trace і Zoom.

 

x1=-3.0213 x2=0.0745 x3=4.8075

2. Розв'язання за допомогою функції root.

Початкові наближення обрані з графіка:

 

 

3. Розв'язання за допомогою функції polyroots.

 

4. Розв'язання за допомогою блока Given... Find.

Початкові наближення обрані з графіка:

 

Лабораторна робота № 5

 

Розв'язання системи нелінійних рівнянь

 

Постановка задачі

Розглянемо систему n нелінійних рівнянь з n невідомими

f_i(x₁, x₂, …, x_n) = 0 (i = 1, 2, …, n),

де f_i – деякі алгебраїчні або трансцендентні функції. Позначивши x = (x₁, x₂, …, x_n) і f = (f₁, f₂, …, f_n), систему нелінійних рівнянь запишемо у векторній формі

 

f (x) = 0.

 

Розв'язання даної системи нелінійних рівнянь полягає у знаходженні таких векторів х, що перетворюють систему в тотожність.

Завдання

 

Дано систему нелінійних рівнянь:

 

 

Розв'язати цю систему:

1) графічним методом;

2) за допомогою розв'язувального блока Given... Find.

 

Порядок виконання

 

1. Графічне розв'язання.

З першого рівняння виражаємо y через x. Оскільки з y добувається квадратний корінь, то одержимо дві залежності – ya(xa) і yb(xb). З другого рівняння виразимо x через y. Отриману залежність позначимо y1(x1). Визначимо функції користувача:

 

 

Інтервал по осі ординат був установлений вручну:

 

Розв'язок знаходиться у вікні інструмента X-Y Trace:

 

 

x=0,53656; y=2,3442.

2. Розв'язання за допомогою блока Given... Find.

Початкові наближення вибираємо з графічного розв'язання:

 

 

Лабораторна робота № 6

 

Розв'язання задачі Коші для звичайного диференціального рівняння першого порядку

 

Постановка задачі

Дано звичайне диференціальне рівняння першого порядку

 

у' = f(x,y).

 

Потрібно знайти розв'язок y = y(x) цього рівняння, що задовольняє початковій умові

 

y(x₀) = y₀.

 

Така задача називається задачею Коші.

Завдання

Знайти розв'язок задачі Коші для звичайного диференціального рівняння (ОДУ)

 

у'=x+y,

 

з початковою умовою y(0)=2 на відрізку [1;2] з кроком h і побудувати графік розв'язку ОДУ.

 

Порядок виконання

 

1. Розв'язання рівняння методом Рунге-Кутта з постійним кроком за допомогою вбудованої функції rkfixed.

Права частина ОДУ:

 

 

Початкова умова:

 

 

Початок відрізка інтегрування:

 

 

Кінець відрізка інтегрування:

 

 

Кількість точок, у яких визначається розв'язок:

 

 

Визначаємо наближені значення функції в заданих точках:

 

 

2. Розв'язання рівняння методом Рунге-Кутта з перемінним кроком за допомогою вбудованої функції rkadapt.

Точність розв'язку:

 

 

Мінімальний припустимий крок розв'язання:

 

 

Обчислення наближених значень функції:

 

 

3. Розв'язання рівняння за допомогою вбудованої функції odesolve.

 

 

4. Графіки знайдених розв'язків ОДУ.

 

 

Лабораторна робота № 7

 

Розв'язання задачі Коші для системи звичайних диференціальних рівнянь

 

Постановка задачі

Задача Коші для системи звичайних диференціальних рівнянь

 

 

полягає у знаходженні частинного розв'язку y₁(x), y₂(x), …, y_n(x), що задовольняє початковим умовам y₁(x₀) = y₁₀, y₂(x₀) = y₂₀, …, y_n(x₀) = y_n0...

 

Завдання

 

Знайти розв'язок задачі Коші для системи звичайних диференціальних рівнянь (СОДУ)

 

з початковою умовою y₁(0)=-1, y₂(0)=1 на відрізку [0;3] з кроком h і побудувати графіки розв'язків.

Порядок виконання

1. Розв'язання задачі Коші методом Рунге-Кутта з постійним кроком.

 

Система диференціальних рівнянь:

 

 

Вектор початкових умов:

 

 

Кількість точок:

 

 

Розв'язок системи диференціальних рівнянь:

 

 

2. Розв'язання задачі Коші методом Рунге-Кутта з перемінним кроком.

 

 

2. Графіки розв'язків з використанням функцій rkfixed і rkadapt.

 

 

Лабораторна робота №8

Інтерполяція функцій

 

Постановка задачі

Нехай деяка функція y = f(x) задана таблицею

 

x0	x1	x2	…	xn
y0	y1	y2	…	yn

 

Потрібно знайти многочлен P_n(x) ступеня n, що приймає в заданих точках x_i (i = 0, 1, 2, …, n) ті ж значення, тобто такий, що

 

P_n(x_i) = f(x_i) = y_i (i = 0, 1, 2, …, n)...

 

Завдання

Дано функцію в табличному вигляді, необхідно:

1. Одержати інтерполяційний многочлен Лагранжа.

2. Записати інтерполяційний многочлен у загальному виді.

3. Виконати інтерполяцію методом Ван-дер-Монда.

4. Виконати інтерполяцію за допомогою вбудованих функцій.

5. Обчислити наближені значення функції в трьох міжвузлових точках.

6. Побудувати графіки заданої функції й отриманих інтерполяційних многочленів.

 

Порядок виконання

Вихідні дані:

 

1. Використовуючи формулу Лагранжа, складемо інтерполяційний многочлен.

 

Спростимо інтерполяційний многочлен, застосувавши директиви simplify і float панелі symbolic keyword toolbar:

 

 

2. Інтерполяційний многочлен у загальному вигляді.

 

3. Побудова інтерполяційного многочлена методом Ван-дер-Монда.

 

4. Інтерполяція за допомогою вбудованих функцій.

4.1. Лінійна інтерполяція.

 

4.2. Кубічна сплайн-інтерполяція.

 

5. Значення функції в трьох міжвузлових точках: Х1=1,5; Х2=2,5; Х3=7,5.

 

6. Побудова графіків вихідної залежності X-Y і функцій f1(x), f4(x), f5(x).

 

 

 

Лабораторна робота № 9