
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійна і квадратична апроксимаціяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Постановка задачі Задача наближення (апроксимації) полягає в заміні функціональної залежності, заданої на множині XÍR у вигляді таблиці, графіка, формули або в неявному вигляді, більш простою наближуваною функцією. Найбільш ефективним методом побудови найкращого середнього квадратичного наближення є метод найменших квадратів. Завдання
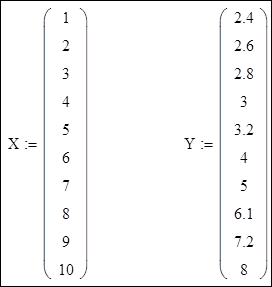
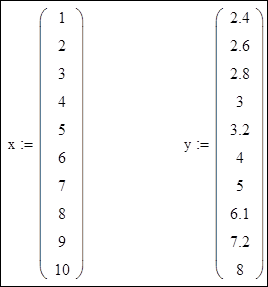
Виконати апроксимацію функції, заданої в табличному вигляді многочленами першого і другого ступеня. Порядок виконання Вихідні дані:
1. Лінійна апроксимація функції. 1.1. Визначення коефіцієнтів апроксимуючого многочлена першого ступеня y=a+bx. Система нормальних рівнянь:
Кількість пар даних:
Розв'язання:
1.2. Визначення коефіцієнтів a, b за допомогою функцій intercept і slope.
Залежність між Xi і Yi близька до лінійного, тому що коефіцієнт кореляції r близький до 1:
Визначаємо апроксимуючу функцію:
Графіки апроксимуючого многочлена і вихідних точок:
2. Квадратична апроксимація. У якості вихідних даних візьмемо табличну залежність з 1-го пункту. Шукаємо апроксимуючу функцію у виді:
Ступінь многочлена:
Визначаємо коефіцієнти апроксимуючого многочлена:
Задамо діапазон зміни х такий же, як і для вектора Х:
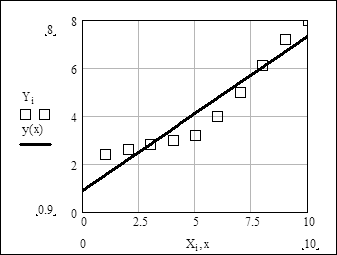
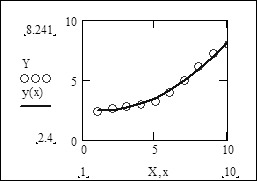
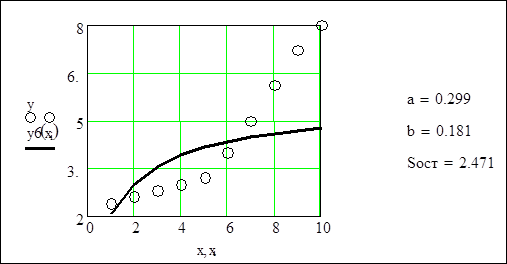
Побудуємо графіки табличної залежності X-Y і апроксимуючого многочлена y(x):
Для оцінки якості отриманого розв'язку обчислимо коефіцієнт варіації:
Помітимо, що функція regress може бути використана для визначення коефіцієнтів апроксимуючих многочленів більш високого ступеня. Однак використовувати многочлени ступеня вище п'ятого не рекомендується.
Лабораторна робота № 10 Апроксимація у виді гіперболічної, показникової, степеневої і дрібно-раціональної функцій
Завдання Для функції, заданої таблицею, провести апроксимацію у вигляді гіперболічної, показникової, степеневої і дрібно-раціональної функцій.
Порядок виконання
Вихідні дані:
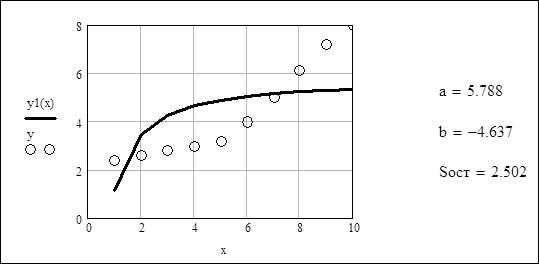
1. Гіперболічна функція y = a + b/x.
Перехід до нових змінних:
Розв'язання:
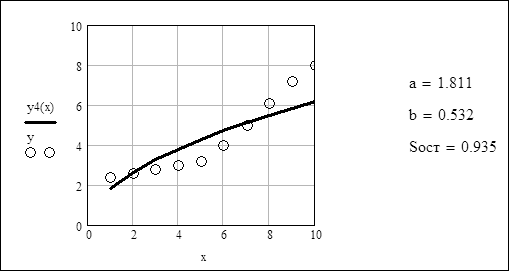
Аналіз отриманих результатів:
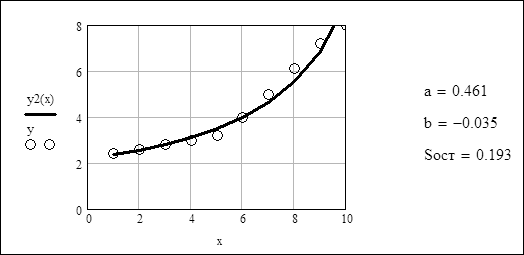
2. Гіперболічна функція y=1/(a+bx). Перехід до нових змінних:
Розв'язання:
Аналіз отриманих результатів:
3. Експонентна функція y=a е bx. Перехід до нових змінних:
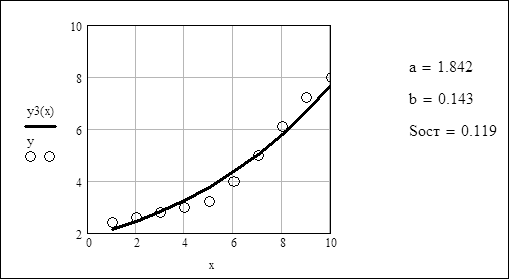
Розв'язання:
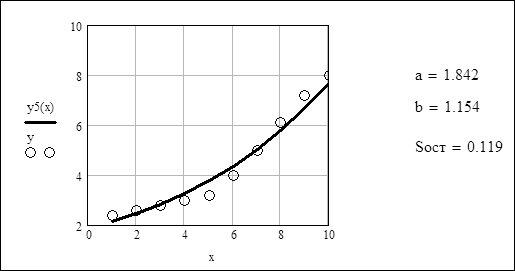
Аналіз отриманих результатів:
4. Степенева функція y =a x b. Перехід до нових змінних:
Розв'язання:
Аналіз отриманих результатів:
5. Показникова функція y = abx. Перехід до нових змінних:
Розв'язання:
Аналіз отриманих результатів:
6. Дрібно-раціональна функція y=t/(a+bt). Перехід до нових змінних:
Розв'язання:
Аналіз отриманих результатів:
Результати обчислень зведені в таблицю:
ДОДАТОК
Завдання до лабораторної роботи №1,2 Виконайте завдання за зразком, наведеним у лабораторних роботах №1,2. Для лабораторної роботи №1 матриці А і В наведені нижче. Для лабораторної роботи №2 матриця А – коефіцієнти при невідомих у системі лінійних рівнянь; B – матриця правих частин цієї системи:
де а=0,01×k; k – номер варіанта.
Завдання до лабораторної роботи №3 Побудувати графіки функцій у декартовій системі координат за варіантами завдань до лабораторної роботи №4. Повторити приклади побудови графіків за пунктами 2-3.
Завдання до лабораторної роботи №4
Знайти корінь нелінійного рівняння на заданому інтервалі.
Завдання до лабораторної роботи №5
Використовуючи задане початкове наближення, знайти розв'язок системи нелінійних рівнянь.
Завдання до лабораторної роботи №6
Розв'язати задачу Коші для звичайного диференціального рівняння.
Завдання до лабораторної роботи №7
Розв'язати задачу Коші для системи двох звичайних диференціальних рівнянь.
Завдання до лабораторної роботи №8
За зразком прикладів, що містяться у лабораторній роботі №8, побудувати інтерполяційні многочлени для даних, наведених нижче.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 1217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.114 (0.007 с.) |

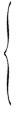
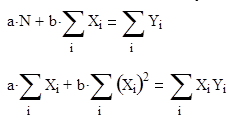
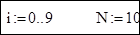
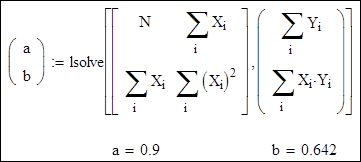
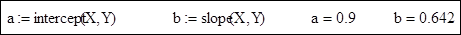
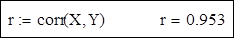
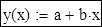
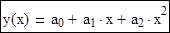
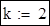
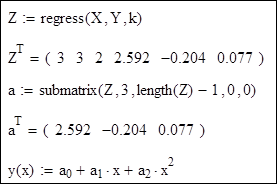
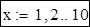
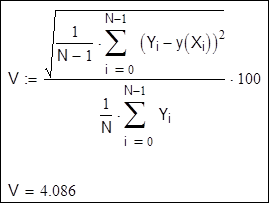


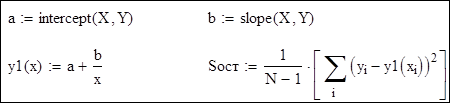

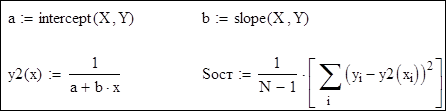
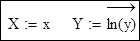
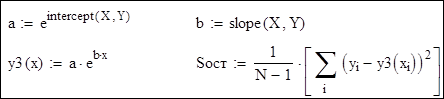

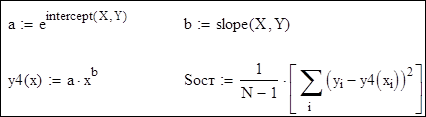

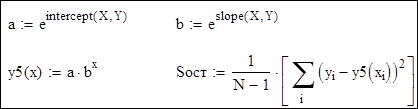

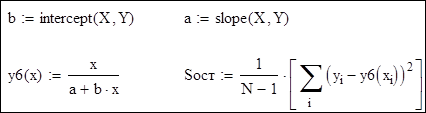
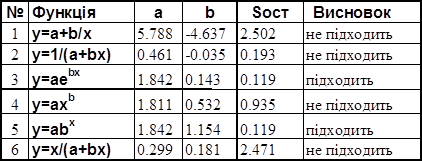
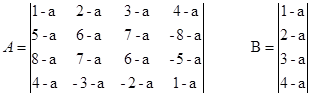
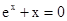
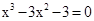
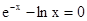
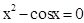
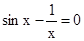
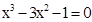
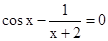
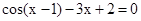
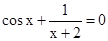
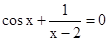
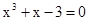
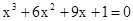
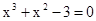
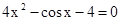
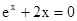
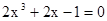
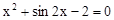
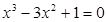
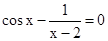
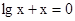
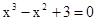
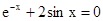
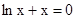
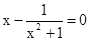
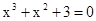
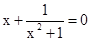
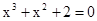
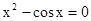
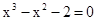
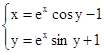 M0(-0,9; 1,4)
M0(-0,9; 1,4)
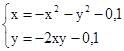 M0(0;0)
M0(0;0)
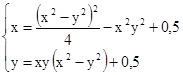 M0(1;1)
M0(1;1)
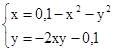 M0(0;0)
M0(0;0)
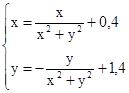 M0(1;1)
M0(1;1)
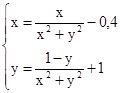 M0(-1;1)
M0(-1;1)
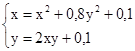 M0(0;0)
M0(0;0)
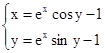 M0(-0,9; 1,4)
M0(-0,9; 1,4)
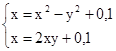 M0(0;0)
M0(0;0)
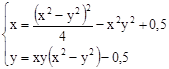 M0(0,5;-0,5)
M0(0,5;-0,5)
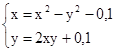 M0(0;0)
M0(0;0)
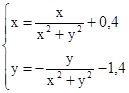 M0(1;-1)
M0(1;-1)
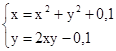 M0(0;0)
M0(0;0)
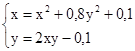 M0(0;0)
M0(0;0)
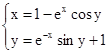 M0(0,9; 1,4)
M0(0,9; 1,4)
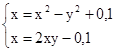 M0(0;0)
M0(0;0)
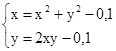 M0(0;0)
M0(0;0)
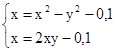 M0(0;0)
M0(0;0)
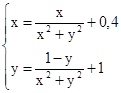 M0(1;1)
M0(1;1)
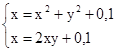 M0(0;0)
M0(0;0)
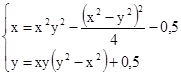 M0(-0,5; 0,5)
M0(-0,5; 0,5)
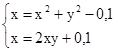 M0(0;0)
M0(0;0)
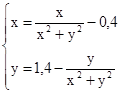 M0(-1; 1)
M0(-1; 1)
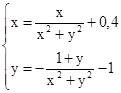 M0(1;-1)
M0(1;-1)
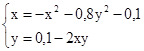 M0(0;0)
M0(0;0)
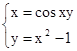 M0(1;1)
M0(1;1)
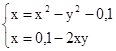 M0(0;0)
M0(0;0)
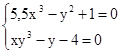 M0(1;1)
M0(1;1)
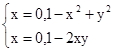 M0(0;0)
M0(0;0)
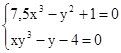 M0(1;1)
M0(1;1)
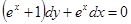
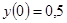
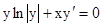
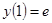
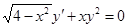
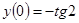
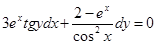
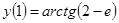
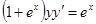
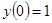
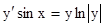
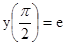
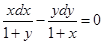
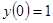
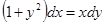
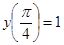
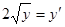
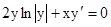
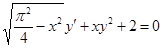
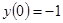
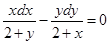
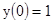
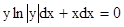
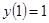
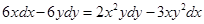
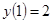
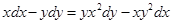
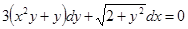
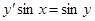
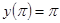
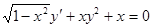
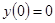
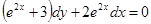
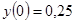
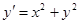
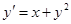
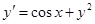
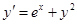
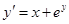
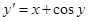
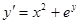
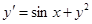
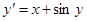
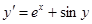
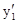
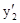
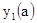
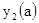
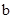
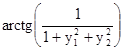
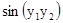
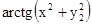
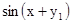
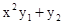
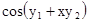
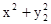
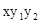
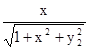
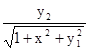
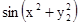
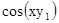
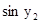
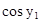
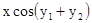
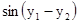
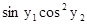
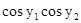
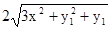
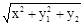
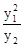
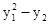
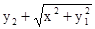
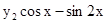
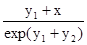
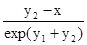
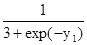
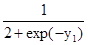
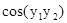
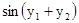
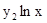
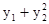
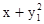
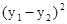
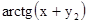
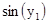
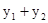
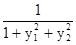
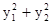
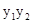
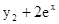
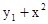
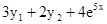
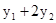
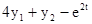
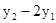
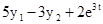
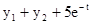
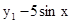
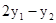
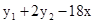
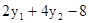
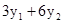
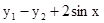
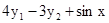
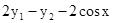
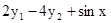
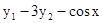
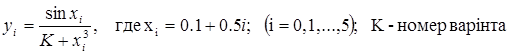 .
.


